Over the past few months the idea of using blockchains as data availability “engines” to post state transitions, rather than execute them, has gotten more traction lately. However much of this discussion hasn’t considered what an optimal chain designed exclusively for data availability and nothing else would look like, and what properties it would have. Such a chain could potentially be implemented as an Ethereum sidechain. Last year I proposed one. I’ve done some further work on this and uploaded a draft paper at https://arxiv.org/abs/1905.09274 and a prototype at https://github.com/musalbas/lazyledger-prototype. I’ll summarise it here.
Reducing block verification to data availability verification
We can build a blockchain where the only rule that determines whether a block is valid or not is whether the data behind that block is available or not. Consequently, consensus nodes and block producers don’t have to process or care at all what messages are actually inside the block. You can thus reduce the problem of block verification to data availability verification. We know how to do data availability verification of blocks with a O(\sqrt{\mathsf{blocksize}} + log(\sqrt{\mathsf{blocksize}})) bandwidth cost, using data availability proofs that use erasure coding and sampling. Nodes who want to verify that a block is available need to sample a fixed number of chunks to get their desired data availability probability, plus Merkle proofs for those chunks (from row/column roots) which are each log(\sqrt{\mathsf{blocksize}}) sized, plus 2\sqrt{\mathsf{blocksize}} row and column Merkle roots.
Note that this isn’t quite magic, because you still need to assume a minimum number of nodes making sample requests, so that the network can recover the full block, just like in a peer-to-peer file-sharing network such as BitTorrent. So if you want to increase your block size, you either need to make sure that there are enough nodes in your network, or increase the number of samples each node makes (which would no longer make it sub-linear), or perhaps a mixture of both.
What greatly interests me about this, is that you therefore have a system whose throughput increases by adding nodes that are not participating in the consensus or producing blocks. If you increase the number of nodes making samples, you can increase maximum safe block size. This would be similar to for example if the throughput of Bitcoin increased by adding more non-mining full nodes. Effectively by removing any need to do state transition execution to verify blocks, and making data availability the only prerequisite of block validity, we can have similar scalability properties to peer-to-peer filesharing systems like BitTorrent, e.g. more nodes = more capacity. (Note that you can’t have the system automatically “count” nodes and adjust block size based on that since they could easily be Sybils, however.)
Sovereign client-side applications
Since no transactions are executed by block producers, and invalid transactions may be posted on the chain, all transaction execution is done by the actual end-users of each application (smart contract), similar to how Mastercoin uses Bitcoin as a base layer for posting messages. However, we could create an application model that supports arbitrary applications defined by clients who are using the blockchain as a place to just post messages. What’s kind of neat about this is that because all the application logic is executed client-side, applications can be written in any arbitrary language or environment, since they’re not executed by the chain.
The main important principal here is application state sovereignty: client nodes must be able to execute all of the messages relevant to the applications they use to compute the state for their applications, without needing to execute messages from other applications, unless other specific applications are explicitly declared as dependencies (in which case the dependency application’s messages are considered relevant).
This means that if there are two applications A and B using the chain that are “independent” from each other, users of application A should not have to download or process the data of B, so if B suddenly becomes more popular, the workload for users of application A stays roughly the same, and vice versa.
Philosophically, this can be thought of as a system of ‘virtual’ sidechains that live on the same chain, in the sense that transactions associated with each application only need to be processed by users of those applications, similar to the fact that only users of a specific sidechain need to process transactions of that sidechain. However, because all applications share the same chain, the availability of the data of all their transactions are equally and uniformly guaranteed by the same consensus group, unlike in traditional sidechains where each sidechain may have a different (smaller) consensus group.
An interesting consequence of this is that as application logic is defined and interpreted off-chain, if some users of an application wanted to update an application’s logic or state, they can do so without requiring a hard fork of the chain. If other users don’t follow the update, the two groups of users will have different states for the same applications, which is like an “off-chain” hard fork.
Efficient per-application message retrieval
To help clients/end-users get the complete set of messages/transactions per block for their applications, without having to download the messages of other applications, we can construct our block headers to allow nodes with the complete set of data (storage node) to facilitate this.
Firstly, each application assigns itself a ‘namespace identifier’, such that any message M included in a block can be parsed by some function \mathsf{namespace}(M) = \mathsf{nid} to get its namespace identifier \mathsf{nid}. Then, when computing the Merkle root of all the messages in the block to use in the block header, we can use an ordered Merkle tree where each node is flagged by the range of namespaces that can be found in its reachable leafs. In the example Merkle tree below, \mathsf{namespace}(M) simply returns the first four hex characters in the message. If the Merkle tree is constructed incorrectly (e.g. not ordered correctly or flagged with incorrect namespaces), then the data availability proof should fail (e.g. there would be a fraud proof of incorrectly generated extended data).
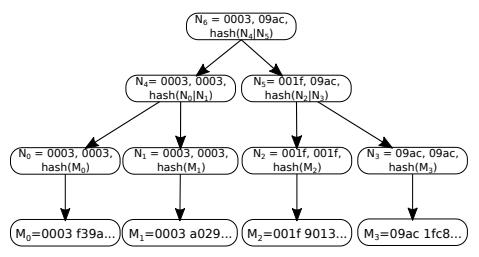
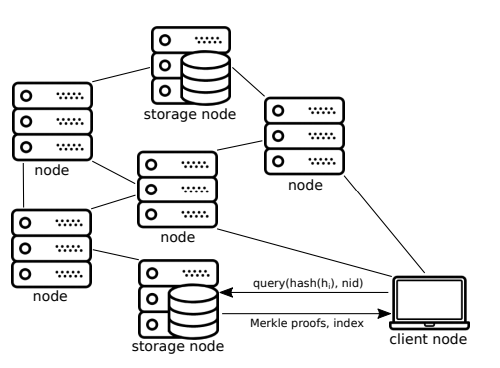
Clients can then query storage nodes for messages of specific namespaces, and can easily verify that the storage node has returned the complete set of messages for a block by reading the flags in the nodes of the proofs.
DoS-resistance
Transaction fees and maximum block sizes are possible under this model without effecting application state sovereignty; see paper for more details. This is necessary to disincentivise users from flooding other applications’ namespaces with garbage.
tl;dr/summary
We can have a dedicated data availability blockchain with the following properties:
- “Fully verifying” a block (in the sense of a full node) has a O(\sqrt{\mathsf{blocksize}} + log(\sqrt{\mathsf{blocksize}})) bandwidth cost, using data availability proofs based on erasure coding and sampling.
- Similar to a peer-to-peer file-sharing network, the transaction throughput of the blockchain can “securely” increase by adding more nodes to the network that are not participating in block production or consensus.
- Users can download and post state transitions to the blockchain for their own “sovereign” applications, without downloading the state transitions for other applications.
- Changing application logic does not require a hard fork of the chain, as application logic is defined and interpreted off-chain.
