Not sure if this was the intent of the signaling approach but I can see how in the case of Gold the signals from the early kings/emperors/chiefs were strong in terms of resources expended to accumulate. Over time these signals have diminished and today are close to zero.
The only time a similar signal occurs with cryptos is at launch. Where is the 2% ongoing signal coming from
Gold is durable, scarce, uniform (with cheap Archimedean authentication), and still quite valuable in industrial applications, of which consensus âsafe havenâ is a non-trivial one - even discounting the exuberance evident in ZH comments and cable news commercials. Coin is coin. Good riddance to gold as numĂŠraire, though.
[McKinnon 1993] The rules of the game: international money in historical perspective
VII. Whereof one cannot speak, thereof one must be silent.
Note: kinda tired, this might all be terrible and incoherent.
Iâm not sure you need much more than Kaldor 1957 (see at 619-621!) to make a âmarketing as obtaining steady stateâ case - like, I think I get where youâre going with rate manifold RM if your k is âworkâ closer to something like Solowâs capital-labor ratio (see also Jones & Romer 2010) than an element of Ramsey 1928âs eternal community in K.
But if itâs cycles and you wanted to have some fun with samplingâŚ
I am a little confused by denoting âsignal strengthâ (power of claim pool) by M and not P. Is it âmoneyâ in the way you want to do VoM in the time domain when you move to a signaling context, really? Sauer 2016 (at 128) is as close to on point as I can seem to find on that question.
But I do see how signal styles could work with a model of spheres of influence, of radius of trust R with distribution[s] Î of projections from stationary source (origin) O (at 9-10). Map of defaults D corresponding to equilibrium fiber bundle of expectations E under condition Dá´š (Friedman 2014; see also Hohfeld 1917; cf. Simons & Sullivan 2007, Kagan & Barron 2001) makes enough sense to me, informally.
[Samuelson 1968] A catenary turnpike theorem involving consumption and the Golden Rule
https://books.google.com/books?id=xisb9usg790C&pg=PA93
Pondering why Vitalik is spending cycles on this topic. Perhaps to help guide the ecosystem for various tokens as well as platform feature set? Perhaps to help develop thinking about whether ETH ecosystem ultimately needs a mechanism to burn tokens? But shouldnât ETH derive the majority of its valuation through its utility and not its âstore of valueâ properties?
The thinking seems sound, but curious why cycles are being spent developing this thought vector.
The issue that I am trying to understand is how the value of ETH relates to the applications built on it and if the burning of ETH is necessary to ensure âadequateâ rent. The whole âstore of valueâ/fiat currency angle is really a BTC issue and as far as ETH and other utility tokens go, a side show.
Perhaps combining the utility/fees argument and looking at valuation through an optionality lens would be useful. If there are X potential use cases that expand ETH transaction fees by Y each, then the net present value (allbeit to miners) in simple terms is the discounted time series X*Y. But from an optionality perspective we have to add an option premium associated with each use case. I argue that the premiums today take into consideration the rise of network valuations over the last few years (Metcalfâs law is now driving tech valuations, per google/facebook, etc.). So options on promising ideas that have the potential to create large networks are gaining premium. With pivots in biz models expected, we then have options on options. This is how I look at ETH as an investor.
Letâs say I am a passive investor in ETH (i.e. no mining): how should I view transaction fees paid to miners (which btw dilutes me) ? What am I missingâŚ
Good point. Best argument I have heard is that fees are paid to secure the network and provide compute services. Think of cost of AWS+people working in cyber security jobs at companies, itâs a lot of money. So rather than each company contracting with AWS, as an example, and hiring their own cybersecurity team we have a shared resource. The thinking is that this shared resource enables the biz models/startups deploying on this model to outperform others using non shared resources. So excess returns to these firms. The question I am struggling with is how are these returns are valued as the ways they are monetized and provided to ETH or ethereum based tokens is based upon biz models are all over the place. Further, even if you could clearly forecast these fees for a firm/biz model, fundamental analysis (DCF of expected future dividends) has broken down in terms of financial instrument valuations over last decade in favor of momentum based valuations. So it looks like investments, at least today, are being valued based on momentum and momentum is built on signaling as per above. Which leads me back to options theoryâŚthat the possibility of excess gains is highly valued. Counter intuitively, volatility actually increase the value of the implicit call option in this space, as opposed to reducing perceived value in most investments.
So fees paid to miners is a COST to me as an ETH investor (I agree it is necessary). I am still struggling with the revenue stream. I agree that option theory vs DCF will be more useful. In fact the only way I can see this right now is as an option on an option (of some future revenue stream)
Iâm not convinced that âbecause of this expectation people buy (or refrain from selling) the token, causing the prophecy to come trueâ is a long-run equilibrium. If it were a stable equilibrium among a set of SoV investors, their wealth would decline relative to an alternative set of SoV investors who seek yield (staking high-velocity chains). Setting rational expectations aside, the behavioural trait is a long-run loser even if the these behavioural traits exist and create local signalling equilibria. The trait will become an ever-decreasing proportion of total wealth. No âclassical economicsâ needed for this conclusion 
Historically, pure scarcity assets have been a poor vehicle of wealth preservation because economies grow and wealth is created through trade. Want your wealth to grow with it, you need to participante in some of the trade. Only in backward, low/no growth economies do the holders of non-income-generating scarcity outperform. Itâs not at all clear to me why the reasons behind this historical pattern change because itâs crypto value.
So the âalternative storyâ makes more sense. But Iâm struggling with the version where SoV-demand earns yield through fee burning and stakers get paid through inflation. That looks like a useless subsidy to unstaked-low-velocity-coin-holders that lowers security (from what it could be if only stakers get the fee). If fees exceed the inflation rate, then high-velocity coin holders are subsidising low-velocity coin holders. Why wouldnât the former just move to an identical chain that differs only in the fee economics (stakers get all the fee)? After all, if the coinâs value is the NPV of fees, itâs the behaviour of the high-velocity coin holders who have a disproportionate influence on the relative coin value between competing chains.
The topic is more complicated that this of course, because there are other properties of the protocol that are relevant. E.g., high velocity value might gravitate towards protocols with smaller validator sets and fast finality (esp cross-chain), censorship-resistance and availability favour large validator sets, and privacy⌠so itâs not âjustâ a story of fees / value-at-stake. But I do think weâll sharpen our analysis of mechanism design if the âstandard modelâ assumes SoV-demand follows yield, rather than muddying the waters with theories of signalling equilibria that happen to have some emperical fit in a trendy, bull market. After all, decentralised protocol design is all about designing for the long-run.
I agree. In addition to obviously favouring proof-of-stake and usage with transaction fees, this also favours reducing issuance (in the form of block rewards to miners/validators), which is not directly explicated in your post, but which you have touched on elsewhere.
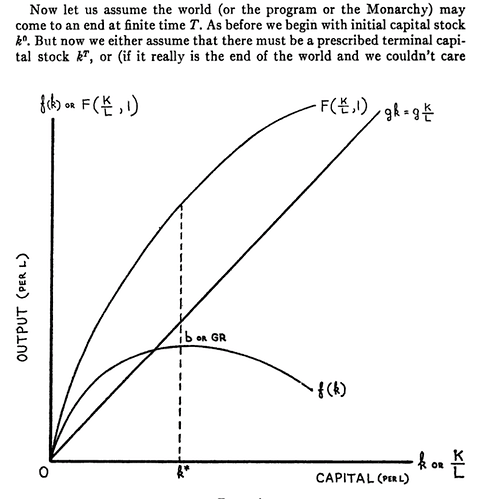
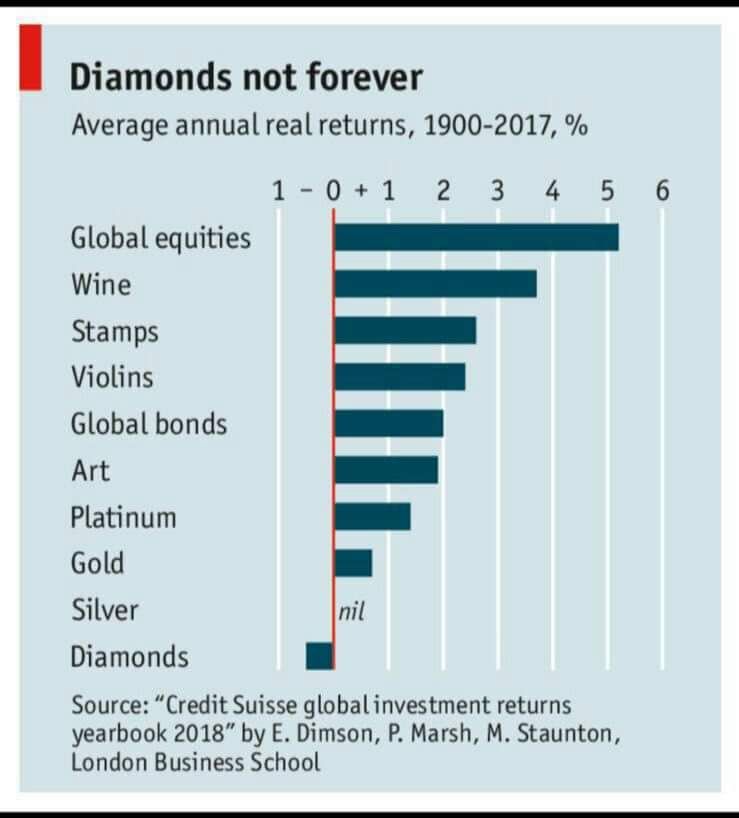
Apologies if this post is a little old now, but i found it fascinating and thought your ideas were really interesting and I think I can help out.
I first analyse the âstore of valueâ argument. If the assertion that is a token with no utility whatsoever should be able to maintain value indefinitely then I think this is provably false. The result is directly drawn from game theory and the nature of zero sum games. Classic economic theory tells us that all zero sum games are unstable (must end) because there is no Nash equilibrium strategy other than avoiding play. This is true despite the potential for new joiners and despite any external conditions (such as economic growth). In this case, âendâ can literally be taken to mean trading must stop. That is - there is one stable Nash equilibrium - a zero value for the âuselessâ coin.
Back to the main question of this thread as I saw it. The question as it is originally asked is actually one around valuation. Asking âwhich coins are a store of valueâ is to me, very similar to asking, âwhich coins are valuableâ.
We tend to think of the market as being separated into two types of transactors - one where the main purpose is speculative gains - one where the main purpose is to derive some utility through the holding of a token.
For me, there are several asset valuation models that are potentially applicable for a cryptocurrency such as bitcoin, Ethereum, or Nano. There applicability is actually dependent on whether we are analysing competitive or monopoly markets and I think there may be differences here between the examples listed. Letâs consider a few methods.
First, there is the valuation of standard (FIAT) currencies. Iâm going to talk briefly about the concept of a carry trade - so skip this paragraph if you are familiar. Although it is thought that the vast majority of transactions in FIAT currency markets are speculative, this is generally considered to have a short term impact on the currency valuation itself. Normal FIAT currencies can be thought of as monopoly markets because they allow access to interest rates and because interest rates are set separately by different central banks. For example, a holder of YEN cannot simply earn a USD interest rates on their YEN. They must first convert their YEN into USD to earn the USD rate - and then back again. This process is fairly common and is referred to as a carry trade. It sets the long term direction of exchange rates.
My point in saying all this is not necessarily to explain the carry trade, which I am sure many of you are aware of, but rather to say that although the majority of trades are speculative, the actual long term value of the currencies actually tracks the carry trade fairly closely. That is to say - currency markets are not driven by speculators - but actually directly driven by those seeking to use the currency for what it is intended for. To see why this must be the case you need only consider the possible arbitrage opportunities by somebody who borrows YEN, paying YEN interest rates and then performs a carry trade on USD. If exchange rates did not move according to the carry trade it would be possible to make near risk free money like this, indefinitely.
Our analogy in the cryptocurrency space is this: the speculators cannot drive the value. In a way, this confirms our first result - a coin with no utility must have zero value in the end (speculation is not enough).
So now, a model for the valuation of a coin with utility - it is also based on economic theory, a Nash equilibrium. Since we are on ethresear.ch it seems only fitting to use Ethereum as our example. We should consider the scenario where a person buys Ethereum, (as the one, in effect, receiving a service) momentarily forgetting miners and other users.
Now, it could be that the person buying Ethereum is a speculator/âhodlâ type transactor. However, we need to dismiss this notion, because, for reasons discussed it is not possible to identify the Nash equilibrium for such a transactor.
Therefore, we must consider a person or consortium purchasing Ethereum at time t. To make the argument easier, letâs also assume that they then sell the token at time t+1. We are left with the complication that holding the coin for one time period does not actually deliver a value directly. So what has the consortium gained? Well, they have won the right to hold the coin over that time period. It is the value of this right which determines the long run value of Ethereum.
It is, of course, possible to build our Nash Equilibrium based not only on direct financial gains from within the system but also from avoided costs outside the system.
I consider one of the most common use cases for the platform. Suppose that our consortium, who purchased Ethereum is actually running an ICO. In this case, the consortium includes all of the ICO participants. Strictly speaking they are separate entities all with distinct aims, but the example works better by consider them all as a single entity for a moment.
We need only to consider the cost of running the ICO outside of the Ethereum system versus within the system. When viewed as a single unit, the group purchase a lot of Ethereum, send it to another party, receiving a custom token in return. We assume for simplicity, that the party running the ICO then sell all of their Ethereum immediately (although this might not be the case).
It is easy to see that if you treat the entire group of transactors as a single unit, this is the same example as above. For the group, as a whole, the value in holding the token between t and t+1 is actually the same as the difference in cost between running an ICO inside and outside the system. Of course, it also depends on how many tokens are involved which scales this cost. Lets say that there are N Ethereum tokens involved and a total avoided cost of \pi N - that is - it is \pi N cheaper to run the ICO inside Ethereum than it is outside.
If we now call the per token avoided cost as \pi, it follows that a simple valuation for Ethereum emerges. The long term value of one Ethereum in USD should be the profit \pi divided by interest r for one USD.
Of course, there are many possible use cases. The formula only works for the best (most profitable) use case. This is because the largest values of \pi tends to set a value which, in effect, makes other use cases an unaffordable use of Ethereum.
Hope this was helpful and thanks all for reading.
(edit because piN wouldnât show)
I think this is exactly where the original argument breaks down, because cryptos not only compete with other cryptos as SoV, but also with existing, more established stores of value. Every single established SoV has an additional use case providing intrinsic value, and therefore has a leg up against pure SoV-coins for exactly the same reasons as coins with utility.
I.e.,
You mention properties of cryptocurrency that âmake it useful to hold in some quantities (particularly, having risks uncorrelated from risks of stocks, making it useful for diversification, and security properties, one of which is censorship resistance)â. The problem is that the usefulness of each of these still rests on the coin having stable value. You donât want to own a devaluing asset just because it is uncorrelated with stocks (which cryptocurrency obviously isnât, because crypto and stocks both compete with money as SoV and therefore are similarly sensible to interest rates). And you donât care if something worth zero is censorship-resistant.
In conclusion, I doubt that your model is long-term stable under rational expectations, because any event that makes other stores of value more attractive (e.g. rising interest rates, or soaring company profits) will lower the market price of a useless crypto asset, which immediately destroys the self-reinforcing expectation necessary for a stable price.
I am proposing a representative currency that could be a stable store of value based on etherium contracts for a specific type of futures contract (not the derivative type). I am hoping with this integration the value of etherium would resolve to gas and the cost of maintaining the etherium network.
A quick summary of the concept is below. 3 types of representative currencies are described. It is the third one that is the most interesting. Describing the other two is time consuming but required as it clarifies why the third is unique.
The main paper where this concept is sourced: https://www.sap.com/canada/documents/2017/11/382d86c5-e07c-0010-82c7-eda71af511fa.html
There are three types of representative currency that could be traded on a blockchain infrastructure: share-backed currency, for the ownership of a factory; inventory-backed currency, for stored output of that factory; and futures-backed currency, for prepaid forward contracts of the output of that factory.
Share-backed currencies would generate dividends and change in value according to the efficiency and management of the corporation.
Inventory-backed currencies would accrue fees for storage. A monolithic form of inventory-backed currency was the gold standard. The blockchain-based form of inventory-backed currency is distinct in that there would be multiple classes of commodities. The objective of storage would not be to prove wealth, but rather to prevent supply and demand shocks in the specific industry by having a store of the commodity available. Monetizing them would be making use of that requirement for storage.
The third type, futures-backed currencies, has some interesting macro-economic effects. A futures-backed currency issued by a luxury car company would represent a specific model of a car with standard features delivered in three years. There would be several types of futures-backed currency based on the obligations and performance of product and service providers. The value of the held future contract increases as that future comes closer in time. This currency increases in value in the same way that the coupon component of a stripped bond matures. They are pre-paying for services at a discount. Reverse the view of discount and think of it as an interest on a bank deposit. By using futures, the difficulty of asset storage is eliminated from representative money. As well, deflationary spirals triggered by currency hoarding are eliminated.
Individual futures-backed currencies would generate interest that reflects the direct risk without aggregation. Risk averse people would earn less interest by holding currencies in companies with established consumer bases and stable output. Another strategy to reduce risk is to use industry aggregators. An institution that represents a specific industry could issue a currency that is an aggregation of a commodity across several different producers and regions.
Another benefit of aggregation is the timing. Futures-backed currencies have an expiry date when the promised good or service is to be delivered. Aggregated futures-backed currencies would not have an expiry date since they are managed by the institution. It would be an easier currency for an individual to hold without actively participating in the financial market. This is the objective of the aggregator - creating a stable unit of value that represents a consistent basket of future goods.
Aggregations of the three types of currencies would stabilize value and return rate. An aggregation of share-backed currencies would be almost identical to a mutual fund or an exchange traded fund. An aggregation of inventory-backed currency would be similar, but without dividends. These two types of currency would both reflect the value of existing businesses or inventory. An aggregation of futures-backed currency would have an additional benefit: unlike mutual funds of shares, which are traded to optimize growth or income, a âmutual fundâ of futures-backed currencies would be traded to maintain a consistent value through a fixed proportion of futures that are spread across a range of exercise dates.
Adding only the first two types of currency to a blockchain infrastructure would still require a traditional banking industry to facilitate debt, adjust the size of the money supply and to finance new ventures. The third type, futures-backed currency, can replace these functions.
Decentralized automatically adjusting natural interest rates.
You are right.
Passiv staking is not the right way.
The benefits we are striving for are also achievable with Staking Pools.
They allow for everyone to participate and profit from the system, which was the intention of passiv staking.
A very interesting discussion. Here are two factors that havenât been considered:
Duration
USD maybe a good short-term SoV but it is certainly less optimal for longer durations. Conversely, XAU maybe volatile in the short-term but much more robust in the long run.
Predictability
I beg to differ, people are increasingly realizing that BTC can be relied upon. Its hard (vs ETHâs soft) immutability could be a unique feature that fosters trust.
If something is unpredictable, it becomes costly, especially for a larger group of users, to track the change. The simpler the system, the the easier it becomes to trust it as SoV.
PS:
Bitcoin can also function as jewelry as block 448064 evinces.
I disagree with the âsimpler is easier to trustâ as it is too simplistic a reduction. Sorry this gets a bit brambly but it is a Friday.
You can simplify a car by cutting off several safety devices, catalytic converter and efficiency devices. The car is then simpler but doesnât satisfy other requirements.
Simple to use is the key. Perhaps describing it as apparent simplicity to the user. The same two cars, the noisy hack job without a seat-belt and the full functioning model would both have the same simple steering wheel and pedal combination.
The electric car is simpler. Much fewer parts. This is a technological superiority first and secondarily it is simplicity in terms of assembly and number of parts. Looking at the chemical processes and physics needed to get it to work without catching on fire, it is not simple.
It is very hard to make something that is simple, easy to do.
As an example, getting from here to there is simple. You walk.
This is not easy for various reasons. Too far, too cold.
As you try to make it easier, it gets more complex. Big animals, feed, reins, axle grease, oil, fuel, roads, maps, licenses, permits, training, symbols, lights, buttons, knobs, peddles.
To make it simpler after making it easier (helpful), some things become opaque. One pedal makes it go; the other makes it stop. At the point that opacity occurs a system has to be advanced enough to guarantee that what is being made opaque will always work so that the operator always has faith in the operation. For a complex system to become simple, either it becomes stable enough that parts become opaque and simplicity is achieved through masking or the system becomes too complex to be usable and it simplifies as a reaction to instability. The result is a decomposition of the system into the simple constituent parts.
Luckily or unluckily, we as humans seem to thrive on instability and complexity. The rats exposed to complex environments vs. simplified environments always develop brains more curious and adaptable when exposed to complexity. There certainly is a sweet spot because the behavior degrades if the environment is chaotic. Forcing simplicity on some systems is unnatural. Nature is a complex system. The variety that exists in nature ensures that a single point of failure will not destroy everything. Forcing simplicity on something that is naturally complex is approaching the problem with a mono crop solution. Protecting the unnatural state of a mono crop require fertilizer and pest protection. Suddenly this adds complexity to the original simple solution.
When you are trying to make something simple, determine if you are trying to organize a naturally existing chaos, masking the complexity of a stable system or extracting and exposing the core simple tasks in a complex system. Each of these requires different strategies and applying the wrong strategy to the situation can make it worse or even ⌠more complex.
Arguing that Bitcoin is simple and therefore is a better store of value is comparable to only growing one crop. A single point of failure and complex systems will be needed to keep it artificially monolithic.
Sorry, I donât quite follow.
I do not think that a complex problem can be reduced like a complicated one, quite the contrary.
My argument was about predictability. The system that wants to accrue trust has to be comprehended by everyone to reduce uncertainty.
The premise is that we need a way to store value. We agreed that value is subjective. Thus, if the SoV is not a concrete asset, it must be a social construct.
I just reached into my pocket and found a coin. A coin! A 3000 year old technology that we still use as front-end because it is simple and understood.
In my opinion, the real store of value will be an axiomatic meme (or multiple) with no other function, a social consensus of sorts. It needs to boil down to something very simple that reduces uncertainty and can thus be accepted universally. Locke for example argued that silver was âequivalent to all other thingsâ because of âthat estimate which common consent has placed on itâ. - We would still use silver if it worked on the internet.
You confuse productive assets, that may very well be complex (like cars) with pure liquid stores of value.
Your previous explanation is not instructive because all three scenarios, including futures-backed currencies, require a polity to enforce contracts and property rights. Our universal store of value can not be attached to specific stakeholders.
You want something ârealâ that is a liability and arguably more ârationalâ. I argue for something that is as real as the relationships that give it substance (i.e. Bitcoin).
