TL;DR
The Avalanche RANDAO is an improvement of the RANDAO-based RNG. In the classical RANDAO, each proposer can bias the entropy by one bit through the choice of not revealing their pre-committed entropy. We circumvent this problem by gradually constructing larger and larger committees in which every single validator knows the secret to be revealed. Early in the construction, when committees are small, it is easy to influence the outcome, but hard to predict the result. In later stages, knowing the result becomes easier but influencing it becomes near impossible, thus limiting the possibilities for bias. For example, using a tree of 128 proposers, this construction can limit the probability that a colluding fraction of 30% of proposers can bias the entropy by one bit to around 2%.
This post is based on a shared idea with @poemm. Thanks to @barryWhiteHat for input on secret sharing and helping with zero knowledge proofs.
Background
The RANDAO has been considered [RNG exploitability analysis assuming pure RANDAO-based main chain] as a possible RNG for the beacon chain. It is based on the simple idea that each validator commits to a hash onion H(H(H(…S…))) when they enter the validator set. Each time it is their turn to contribute entropy, they reveal one further layer from this onion. Thus, they only have one choice when revealing entropy, to either reveal the precomitted value or to not reveal at all, forgoing the block reward. If a large amount of money is at stake, a validator could choose the latter, as a random roll might give them a better expected return than the entropy they are about to reveal – thus they have the ability to bias the entropy by 1 bit.
However, it has turned out that even this ability to introduce a 1-bit bias on a per-validator level can lead to very significant control when many validators collude. The simple RANDAO-based chain can in fact be completely taken over by 34% of the validators [RANDAO beacon exploitability analysis, round 2]. Nevertheless the RANDAO is still used as a base source of “biasable” entropy, on which the currently favoured construction based on verifiable delay functions can be built [Minimal VDF randomness beacon].
Several attempts have been made to improve on the pure RANDAO construction by reducing the bias. One idea is to have an additional one bit clock, generated from the next reveals of the validators “voting” on whether the current entropy should be used for the next validator selection [Making the RANDAO less influenceable using a random 1 bit clock]. While this construction can reduce the biasability by single validators, it actually greatly increases the influence of large numbers of validators colluding. The original construction based on majority voting could be improved using low influence functions, further decreasing the chances of introducing bias for a single validator, however also weakening the construction to opponents with a large share of validators. Ever since, there has been the question if there are also constructions that could stand up to large coalitions and actually reduce the amount of bias they can introduce.
More recently, a new idea going into the same direction was introduced, in a way bringing the “low influence” to a different level: Letting committees pre-share their secret, so that at the time when the secret has to be revealed, it is enough that any of the validators reveal it, thus limiting the ability of one or even many validators to bias the entropy by not revealing [Limiting Last-Revealer Attacks in Beacon Chain Randomness]. The idea is promising, but it lacked a feasible way to construct these pre-shared secret.
Here we introduce the Avalanche RANDAO, a way to construct a shared secret among many validators, and analyse the biasability of this construction.
Goal
We want to create a scheme with the following properties:
-
The validators agree on a common secret S, that by construction is known to all validators. No validator can construct a valid S without all the participating validators knowing about it
- Ensures that if even a single validator participating in the construction is honest, they will be able to share the common secret when it’s their time
-
The secret S is uniquely determined by the validators participating in the secret-sharing scheme. The only influence a validator can have on it is whether they participate or not
- Minimises the possibilities of validators manipulating the resulting entropy. Keeps the RANDAO property that at best, a single validator can have a single bit of bias by revealing or not.
-
Every validator should be able to prove that the secret was constructed in this way
- When sharing the secret on chain, this proof should be included
-
The construction should go ahead even if some of the validators are not participating or are withholding collaboration part way
- Validators being offline or maliciously not participating should not stop the scheme
-
A part of the committee, even if they are in the majority, should not be able to construct this secret while excluding someone who wants to be inside it if they are online; in other words, anyone in the committee should be able to force their way into the secret as long as they are connected to the network
- If more than 50% of the validators on a committee are in one malicious colluding fraction of validators, they should not be able to construct a secret only they know
Setup
We assume that we have a set of n validators in a committee. Each validator v_n is committed to a secret a_n by means of a suitable scheme (e.g. through a hash \text{sha256}(a_n) or by publishing a_nG where G is an elliptic curve element). This basically means we use the RANDAO construction as our basis, to make sure that validators have minimal choice going through the process.
Diffie-Hellman
Our secret sharing mechanism is based on two-party Diffie-Hellman.
We use the elliptic-curve notation for Diffie-Hellman shared secret construction below. The idea works with any DIffie-Hellman scheme, but the elliptic curve construction will probably fit most naturally with the zero knowledge proofs which are required at each stage to show that the construction of the secret was done correctly.
Avalanche RANDAO construction
The idea is that we create a binary tree of shared secrets, with the property that all of the participants in each subtree know the shared secret of that subtree, while generally people outside do not know it, except if it is shared with them by a validator in that subtree.
In the early stages of building up the tree, when each subtree consists of, say, 1, 2 or 4 validators, it is easy to influence the outcome but difficult to know it, so it is hard to bias.
Once the subtrees become larger, large parties of colluders do actually get a more significant chance of knowing the outcome, but by now the shared secrets are known to so many other validators that it is “too late” to stop it (the avalanche).
At each level of the tree, we use Diffie-Hellman to share the secrets of the two subtrees.
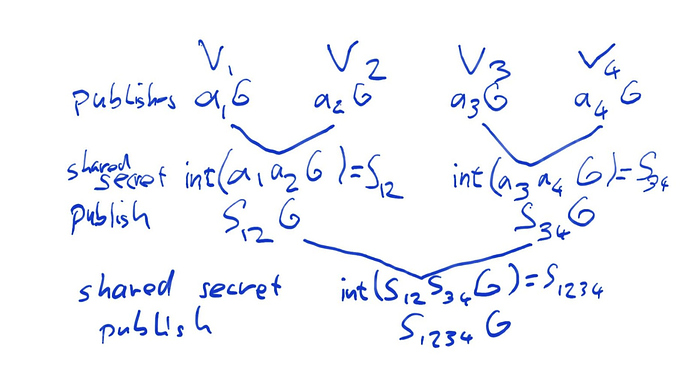
First step
The first step consists of all n=2^m validators publishing their secret commitment a_iG. (Might be part of the pre-commitment already)
Second step:
- v_1 and v_2 compute a_1a_2G, from which they compute a shared (secret) integer S_{12}=\text{int}(a_1a_2G) and publish S_{12}G
- v_3 and v_4 compute a_3a_4G, from which they compute a shared integer S_{34}=\text{int}(a_3a_4G) and publish S_{34}G
- …
- v_{n-1} and v_n compute a_{n-1}a_nG, from which they compute a shared integer S_{n-1,n}=\text{int}(a_{n-1}a_{n}G) and publish S_{n-1,n}G
Note that either of the two validators sharing a secret can compute it for each of these secrets. The collaboration of the other validator is not necessary, but even if they don’t participate they will still be able know the secret.
Third step
In the third step, v_1 and v_2 both know S_{12} as well as S_{34}G; v_3 and v_4 both know S_{34} and S_{12}G. So each of the four can compute S_{12}S_{34}G without participation of any of the other validators. Our third step thus consists of
- v_1, v_2, v_3 and v_4 compute S_{12}S_{34}G, from which they compute a shared integer S_{1234}=\text{int}(S_{12}S_{34}G) and publish S_{1234}G
- v_5, v_6, v_7 and v_8 compute S_{56}S_{78}G, from which they compute a shared integer S_{5678}=\text{int}(S_{56}S_{78}G) and publish S_{5678}G
- …
- v_{n-3}, v_{n-2}, v_{n-1} and v_n compute S_{n-3,n-2}S_{n-1,n}G, from which they compute a shared integer S_{n-3,n-2,n-1,n}=\text{int}(S_{n-3,n-2}S_{n-1,n}G) and publish S_{n-3,n-2,n-1,n}G
nth til last steps
This process carries on until in a final step, there are only two subtrees A and B left, with shared secrets S_A and S_B. The commitments S_AG and S_BG are already shared on chain, so at this point, any validator in the whole committee can compute and share the common secret S_AS_BG which will be used as entropy for the Avalanche RANDAO.
At each step, a zero knowledge proof has to be provided that the computation is indeed correct and no “garbage” or invented values were published. This should be fairly simple using SNARKs as all the computations are very simple EC operations.
Avalanche RANDAO analysis
We want to analyse what influence someone possessing a fraction f of the total stake (a single entity or a coaliton) can have on the randomness of the Avalanche RANDAO.
We can analyse the Avalanche RANDAO by layer. Except for the bottom layer of the tree, a complete analytic expression is very complicated, so we resort to a computer simulation instead. Biasability by layer can be evaluated like this:
- First round (share aiG): Bias possible if the coalition controls v_n as well as one in each pair before; probability of this is f(1-(1-f)^2)^{n/2-1}
- Second round (share S_{i,i+1}G): Bias possible if controlling any pair, one in each group of four before and one in each pair that comes after
- Third round (share S_{i,i+1,i+2,i+3}G): Bias possible if controlling any subtree of four, one in each subtree of four that follows and one in each group of eight that comes before
Here is a python program that uses a Monte-Carlo simulation to estimate the biasability:
import random
import math
import numpy as np
def get_committee(layer, committee_no, compromised_nodes):
layer_subcommittee_size = 2 ** layer
committee = compromised_nodes[layer_subcommittee_size * committee_no:layer_subcommittee_size * (committee_no + 1)]
return committee
def check_committee_infiltrated(layer, committee_no, compromised_nodes):
return any(get_committee(layer, committee_no, compromised_nodes))
def check_committee_compromised(layer, committee_no, compromised_nodes):
return all(get_committee(layer, committee_no, compromised_nodes))
def layer_compromised(layer, compromised_nodes):
layer_subcommittee_size = 2 ** layer
num_nodes = len(compromised_nodes)
for i in range(num_nodes / layer_subcommittee_size):
if check_committee_compromised(layer, i, compromised_nodes):
if all(check_committee_infiltrated(layer, j, compromised_nodes) for j in range(i)):
if all(check_committee_infiltrated(layer + 1, j, compromised_nodes) for j in range((i/2) * 4 + 1, num_nodes / layer_subcommittee_size / 2)):
return True
return False
def layers_compromised(compromised_nodes):
layers = int(math.log(len(compromised_nodes))/math.log(2)) + 1
ret = []
for i in range(layers):
ret.append(layer_compromised(i, compromised_nodes))
ret.append(any(ret))
return map(lambda x: 1 if x else 0, ret)
def generate_random_compromised_notes(f, n):
return [1 if random.random() < f else 0 for i in range(n)]
n = 128
f = 0.3
compromised_nodes_list = [generate_random_compromised_notes(f,n) for i in range(10000)]
results = map(layers_compromised, compromised_nodes_list)
print zip(np.average(results,0),["Layer %d compromised" % i for i in range(8)] + ["Tree compromised"])
Our results so far:
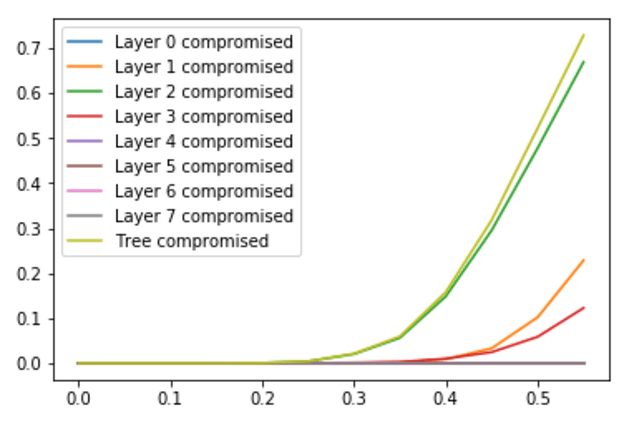
- If the fraction of colluding nodes f<0.5, we get very promising results. For example, for f=0.3 and a tree of 128 validators, the probability that biasing is possible is only 2%, which is a very good result
- As the fraction size approaches f=0.5, the probability of bias always goes to 0.5. In fact, for any tree size, it seems like at f=0.5 we always get >50% probability of being biasable; from other trials it seems plausible that this is some sort of fundamental limit
- The main contribution to the probability of the tree being compromised (biasable) comes from layers in the middle in the tree. As the tree gets larger, the layer that is most likely to be compromised moves up in the tree. (The plots below show the probability of a tree being compromised for different fraction sizes at n=128, 512 and 2048; so with arbitrary large trees we can move the “kink” of the curve more and more to the right)
- Looking at the nodes that contribute to trees being compromised, we might expect that it is the nodes that reveal later in the process that contribute more. Analysis shows that this is indeed the case for small fraction sizes, but for large fractions it is very evenly distributed across the tree. This means there is probably very little to gain by trying other, asymmetrical, tree structures; for large colluding fractions, the complete binary tree seems close to optimal


 Unfortunately, for this construction to work, we need to keep
Unfortunately, for this construction to work, we need to keep