Status: draft, pending verification.
Recommended pre-reading: the original Casper FFG paper: https://arxiv.org/abs/1710.09437
Suppose that we extend Casper FFG as follows.
- Time is broken up into “slots” (periods of
dseconds, eg. d=8). - The validator set is split up ahead of time into N equal-sized slices, which are repeated (eg. slice 3 of the validator set is called to send messages during slots 3, N+3, 2N+3…).
- During each slot, a single validator can propose a block, and the slice of validators corresponding to that slot can vote for it.
- A vote votes both for a block (its “target”) and for that block’s N-1 nearest ancestors (ie. N blocks in total).
- A block is justified if 2/3 of the validator set votes for it (in any of the N slices that include or follow its slot). Note that any block can be justified, not just epoch-transition blocks. The chain keeps track internally of what the “last justified block” is, and votes use this as their “source”. Note also that a chain only accepts votes if their source is the source specified in the chain, which itself is guaranteed to be an ancestor of the head of the chain.
- If a sequence of N+1 blocks that are all part of the same chain is justified, then the earliest block in the sequence is finalized.
- The two slashing conditions are:
- A validator cannot make two distinct votes in the same slot
- A validator cannot make two votes
(s1, t1),(s2, t2), whereslot(s1) < slot(s2) < slot(t2) < slot(t1), whereslot(x)is the “slot number of x” function.
We prove safety as follows. Suppose that two conflicting blocks b1, b2, with [slot(b1) ... slot(b1) + 2N) being the span of slots in which b1 is finalized. Suppose without loss of generality that slot(b2) > slot(b1). Then, there exists some sequence of slots j[0] < j[1] < ... < j[n] representing the justification chain, where j[0] is the last justified checkpoint that is also part of the same chain as b1 (ie. j[1] is the first one that is not), and j[n] = slot(b2). For each j[i], 2/3 of validators made votes whose slot numbers for the target are in [j[i] ... j[i] + N) and for the source are <= j[i-1]. We know such a sequence exists because we know j[n] is justified and justifying any checkpoint requires some previous justified checkpoint. Let j[i] be the highest slot in the sequence where j[i] < slot(b1). We consider three cases:
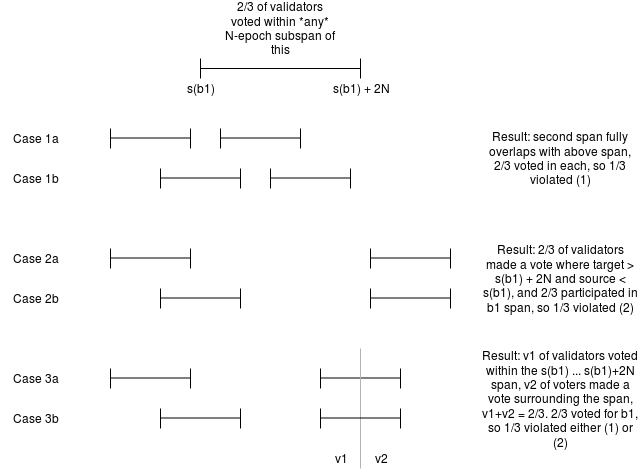
Case 1: If [j[i+1] ... j[i+1] + N) is fully inside [slot(b1) ... slot(b1) + 2N), then there would be 2/3 of validators voting for something in the b2 chain intersecting 2/3 of validators voting for something in the b1 chain, implying at least 1/3 violated (1).
Case 2: If j[i+1] >= slot(b1) + 2N, then 2/3 of validators would have made a vote with a span surrounding (slot(b1), slot(b1) + 2n) and 2/3 of validators a vote with a span within that same range, meaning at least 1/3 violated (2).
Case 3: Now consider the case where slot(b1) + N < j[i+1] < slot(b1) + 2N, so [j[i+1] ... j[i+1] + N) is partially inside and partially outside [slot(b1) ... slot(b1) + 2N). There are now two subsets of validators: a set v1, which made votes surrounding the span (slot(b1), slot(b1) + 2n) and a set v2, which made votes inside of this span. The combined size of v1 and v2 is 2/3, meaning at least 1/3 of them also participated in the b1 chain. These validators therefore violated conditions (1) or (2), or some combination of both.
Plausible liveness can be proven much more easily. Suppose that h1 is the highest justified checkpoint. Then, no honest validator made a block with a source higher than h1. Suppose h2 is the highest slot number used up to this point. Then, 2/3 of validators can justify h2 + N, using h1 as a source, and then proceed to fill the span [h2 + N ... h2 + 3N).
