Faster block/blob propagation in Ethereum

Networking
23

Thanks so much for this nice post! It was a pleasant and interesting read! And definitely a really nice proposal!

How is this a small field? Is almost the order of the scalar one of Ristretto or 25519 already (2^{255}-19).

I wonder if in general you have explored other commitment schemes. If the SRS (trusted setup) is a must-have, then seems only KZG is the other viable option.

  • I wonder if this could be done differently to avoid using EC-based stuff in the networking layer(considering there are plans to migrate to PQ primitives). I’m thinking about Ajtai commitments mostly. But there could be other things worth exploring. Just need to be sure I understand all the properties that this requires to a commitment scheme.
  • Also, worth considering using on the “Don’t care about PQ case” something like: Efficient Elliptic Curve Operations On Microcontrollers With Finite Field Extensions. This allows us to have curves that have extremely tiny fields, yet give us 128-bit security. Thus, enabling us to have all the benefits of small fields with the properties like hash-to-curve etc


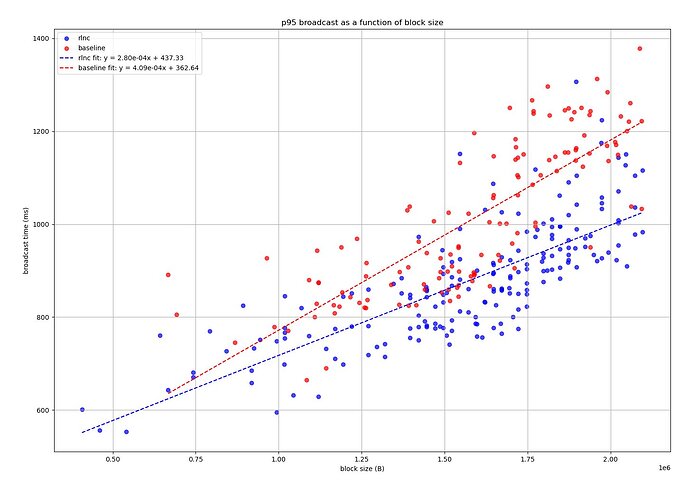
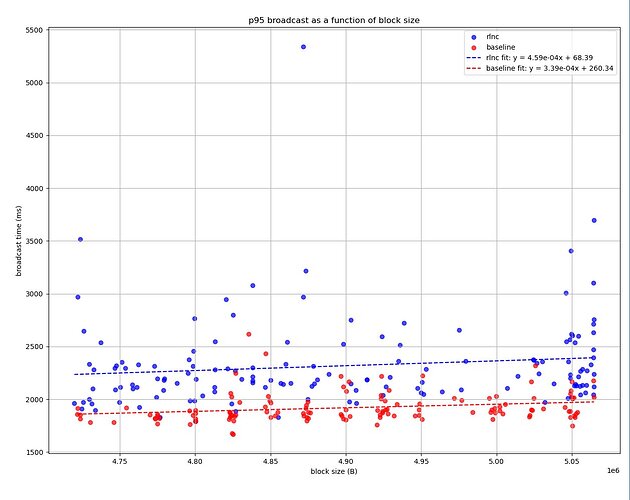
As for RLNC this is definitely a really nice option for gossiping!

I think it’s also important to highlight this metric. RLNC saves us bandwidth undeniably. And it definitely seems to improve converging times. ie. time it takes to the majority of the network to be in sync on latest state sent.
Do you envision any possible improvements in that part? Is already RLNC addressing this problem too? Hence we just ignore this?

24

Apologies, I meant that if we had a field with a small prime characteristic (in the above case 2) then we could have the coefficients be in F_{p^k} and the commitments in F_{p^r} with k << r. This way the commitments are still secure while the coefficients that go over the wire are smaller. For p = 2 I think k = 8 works fine, while still we can use r=256 for secure commitments.

I haven’t considered any other commitment schemes yet and I’m happy and open to look for any of them. The abstract properties I’d like to have are

  • Coefficients need to be small (1 byte is enough)
  • Commitments can be larger but the smaller the better while maintaining security (I suspect it’s hard to do better than 32 bytes here

Yes, we are about to start benching a Prysm implementation, we think we can get big improvements in throughput.

25

This is a great point, which we have researched. Here are the most relevant papers:
For theory
V. Abdrashitov and MĂ©dard, M., “Durable Network Coded Distributed Storage," Allerton 2015
V. Abdrashitov and MĂ©dard, M., “Staying Alive - Network Coding for Data Persistence in Volatile Networks," invited paper, Asilomar 2016
For demonstration
F.H.P. Fitzek, Toth, T., Szabados, A., Pedersen, M.V., Lucani, D.E., Sipos, M., Charaf, H., and MĂ©dard, M., “Implementation and Performance Evaluation of Distributed Cloud Storage Solutions using Random Linear Network Coding," IEEE CoCoNet 2014
We are concerned about the time when the degrees of freedom dip below what is needed for the coded data to be recoverable, which is m. The dofs are given by m, see equation (3) and the discussion at the start of II.B. We are thus concerned (taking W^t as the measure rather than M_t directly, as per (4)) with the case where the rank of W^t becomes m-1. We parametrize the rank for a k as in (12), so we are worried for the rank (c-k)s_c = m-1 where c is the number of nodes, s_c is the storage per node for c nodes. So, we have, ignoring integrality issues, k =c- \frac{m-1}{s_c}. This is the case where one node fails at a time and a new node only connects to a single node to obtain new information, chosen at random (note that it would be much more robust if we connected to more than one, but then we have a messy system like in (9)).

The hitting time for getting to m-1 dofs (failure) is then \frac{\left(c- \frac{m-1}{s_c} \right)(c-1) s_c}{m-1}. Ignoring the -1 for c and m, this is approximately \frac{c^2 s_c}{m}- c , which is basically \frac{c^2 s_c}{m}.

1 Like
26

@MedardDuffy Thanks for all the resources!

I’m curious on whether there is literature on reducing the overhead of RLNC messages? Some concrete questions on that front:

  • Is it possible to avoid sending the full list of random coefficients? For instance, the first node could send a small seed that generates the list of coefficients, but that gets messy quickly when messages need to be re-forwarded and the coefficients must compound.
  • Is there research on more efficiently authenticating the source of RLNC messages? The proposal in this post suggests using N homomorphic commitments and a signature that connects them. Is there literature on more efficient constructions?
3 Likes
27

It feels like a lot of needless complexity to introduce a whole new commitment scheme (pedersen) and a whole new erasure coding algorithm (RLNC), when we already have a perfectly good structure that is being used in Ethereum that satisfies those properties: KZG blob encoding.

KZG blob encoding already creates a very natural built-in way to encode a blob into a (nearly) arbitrary number of chunks, such that a (nearly) arbitrary fraction of them can suffice to reconstruct the original data. We should just reuse that mechanism, and make an effort to also put the block data into blobs (because that allows the block data itself to be verified with DAS, which will allow us to have extremely light clients once we can ZK-EVM prove everything else).

There may be slight efficiency advantages toward hyper-optimizing a different code for each different use case, but those gains intuitively seem like they would be much smaller than the downsides of having 2x the code complexity. We have been trying to fight against ethereum’s growing code complexity and embrace more of an ethos of minimalism for a long time, and this seems like a really natural place to do this.

Additionally, using KZG to split the data for broadcast gives us a lot of potential future synergies with various DAS strategies. For example, suppose that a node receives only samples 0
15 of a blob. That node could immediately confirm all DAS queries to all peerDAS nodes that it listens to that are within that range. This could allow nodes to get DAS confirmations ~1 network latency hop faster, allowing for shorter slot times.

2 Likes
28

You are right in saying that we could use KZG + RS for blocks as well, however, there are well documented advantages for RLNC over RS as a distribution mechanism, some already cited above by @MedardDuffy, but also in this particular case of Ethereum, using a much faster commitment scheme as Pedersen over Ristretto or similar is much more performant than KZG.

Complexity-wise, well, yes, any mechanism that changes the signature (the proposer needs to sign over a header that now includes the commitments) ends up piling complexity. However, this complexity will also be there if we were to use coding on blocks. You can take a look at the full implementation on Prysm here [DO NOT MERGE] Use RLNC for block propagation by potuz · Pull Request #14813 · prysmaticlabs/prysm · GitHub and you will see that most of the complexity is dealing with the signature change, the RLNC part is a rather simple module of matrix multiplication. I stress that most of the changes in having to deal with the signature verification at the chunk level instead of the block level will have to be carried for KZG+RS anyway. The reason we don’t have this problem with blobs is because of @fradamt’s idea of including a Merkle proof of inclusion and bootstrapping the block signature verification, something we cannot do when we are trying to gossip block chunks themselves.

Moreover, a switch over to RLNC will actually simplify a lot the most vulnerable part of client development: the outer p2p libraries: things like “mesh”, heartbeats and keeping track of messages ids become irrelevant (since there are no two equal messages in the network) and all of that code complexity in the layer that is directly exposed to DOS attacks is gone. I have not yet dealt with this part. We rather added an interface to allow go libp2p to send a random message to random peers, so our PoC for benchmark still has a bunch of unnecessary bloat coming directly from gossipsub which hopefully in next iterations we will be able to remove.

If anything, it seems that we could potentially be even bolder and explore other coding mechanisms for DAS itself, compatible with RLNC, and ditch RS entirely.

Edit complementing this reply: Since most of the complexity is in the signature verification being based per-chunk instead of per-block, I think I can take my branch and replace it with RS+KZG and do actual benchmarks of the three methods: gossipsub, RLNC+Pedersen, RS+KZG
 I just need someone to fund the big machine to run Shadow :slight_smile:

29

@asn thank you for the great question. The random coefficients are quite small in overhead, say of the order of 1%. Think of working over a finite field \mathbb{F}_q if working over a prime field or \mathbb{F}_{2^n} for a binary extension field. The data shred is itself a vector, say an element of \mathbb{F}_{2^n}^m. If we work over bytes, which means that n=8 and your shred is 1kB, and you are combining k shreds, say 10 shreds, then your overhead is \frac{k}{m}, so around 1%. The coefficients are changed with recoding, they do not accumulate as you recode.

It is also the case that one can use a random seed for the generation. We have done so in implementations to bring network coding into TCP at the kernel level
J. K. Sundararajan, D. Shah, M. Medard, M. Mitzenmacher and J. Barros, “Network Coding Meets TCP,” IEEE INFOCOM 2009 , Rio de Janeiro, Brazil, 2009, pp. 280-288,
J. K. Sundararajan, D. Shah, M. Medard, M. Mitzenmacher and J. Barros, “Network Coding Meets TCP,” IEEE INFOCOM 2009 , Rio de Janeiro, Brazil, 2009, pp. 280-288
which can be also done in user space over a UDP socket
M. Kim et al ., “Congestion control for coded transport layers,” 2014 IEEE International Conference on Communications (ICC) , Sydney, NSW, Australia, 2014, pp. 1228-1234
or in Quic
F. Michel, A. Cohen, D. Malak, Q. De Coninck, M. MĂ©dard and O. Bonaventure, “FlEC: Enhancing QUIC With Application-Tailored Reliability Mechanisms,” in IEEE/ACM Transactions on Networking , vol. 31, no. 2, pp. 606-619, April 2023.

1 Like
30

On the topic of efficient homomorphism, we have developed code-homomorphic encryption, which maps to Different-Hellman. It is treated in our book and also published in
M. Kim et al ., “On counteracting Byzantine attacks in network coded peer-to-peer networks,” in IEEE Journal on Selected Areas in Communications , vol. 28, no. 5, pp. 692-702, June 2010
which also shows other mechanisms for verification, including simple polynomial hashes,
as well as algebraic watchdog approaches.

1 Like
31

Great work!

Would be nice to added a section on security analysis. What happens if some nodes are Byzantine and deliberately corrupt messages. Does one require some kind of a verification algorithm for block pieces?

32

The system does verify the integrity of the messages, see this reply Faster block/blob propagation in Ethereum - #15 by potuz

33

I’ve been thinking about this more, specially given the scary patent situation with RLNC. Reed-Solomon + KZG does have some benefits in that perhaps you don’t need to send all commitments, you can probably commit to the commitment vector, sign over this. The proposer also attaches a proof of the value of this committed vector for each chunk. So in this case the overhead in the header is just on commitment and one proof, so there’s no linear term in the number of chunks. The tradeoff is that the proposer needs to prepare N KZG proofs, but I think trading off CPU over bandwidth when this can be parallelized, and is mostly computed by the builder, is probably acceptable.

I’ll modify my branch to use this approach and bench against RLNC.

34

For Byzantine detection with RLNC, beyond the reference I provided above which compares all of the following approaches and compares thei overheads in different attack scenarios, here are detailed references for each approach

1/ Approach 1: detection after decoding

T. Ho, Leong, B., Koetter, R., MĂ©dard, M., and Effros, E., “Byzantine Modification Detection in Multicast Networks with Random Network Coding," Special Issue on Information-theoretic Security of the IEEE Transactions on Information Theory, Volume 54, Issue 6, June 2008, pp. 2798-2803

2/ Approach 2: homomorphic detection

F. Zhao, Kalker, T., MĂ©dard, M., and Han, K., “Signatures for Content Distribution with Network Coding,” ISIT (5 pages), July 2007

3/ Approach 3: error-correction (note - one does not need to use outer RS, can use RLNC instead, can explain further, but requires a longer post)

S. Jaggi, Langberg M., Katti S., Ho T., Katabi D., MĂ©dard, M., and Effros, E., “Resilient Network Coding in the Presence of Byzantine Adversaries," Special Issue on Information-theoretic Security of the IEEE Transactions on Information Theory, Volume 54, Issue 6, June 2008, pp. 2596 - 2603

4/ Approach 4: algebraic watchdog (here is for wireless, general principle is the same)

M. Kim, MĂ©dard, M., and Barros, J., “Algebraic Watchdog: Mitigating Misbehavior in Wireless Network Coding," IEEE Journal of Selected Areas in Communications, vol. 29, no. 10, December 2011.

35

Here is another potentially interesting idea for a better protocol based on RLNC:

  • E.g. a node is publishing a message and have started chunks broadcasting
  • A new message appears for publishing
  • The node may start broadcasting linear combinations of chunks from both messages (which could be verifiable exactly the same way)

The upside of this approach is even lower number of duplicates and faster delivery of the second message.
The downside is potentially slower delivery of the first message.

Not sure how it could improve our block/blob use case though.

1 Like