Edit: turns out this idea is already out there, on page 20 of https://eprint.iacr.org/2018/601.pdf. Congrats to Dan Boneh, Benedict Bunz, Joseph Bonnneau and Ben Fisch.
MIMC is a hash function “core” that Zcash is evaluating as a possibility to switch to in the mid-term future pending much more security analysis: https://github.com/zcash/zcash/issues/2233
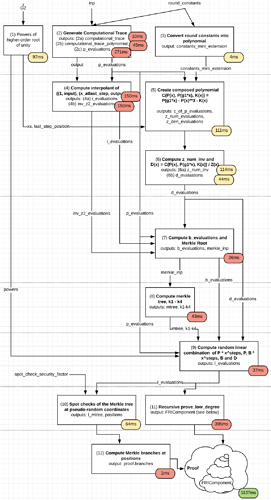
The goal of MIMC is to be maximally SNARK and STARK-friendly, and it does so by building its core primitive to be made up entirely out of simple operations within some finite field. Specifically, MIMC’s permutation function looks as follows:
k_1 k_2
| |
v v
input -----(x->x³)------(xor)------(x->x³)------(xor)---- ..... ----> output
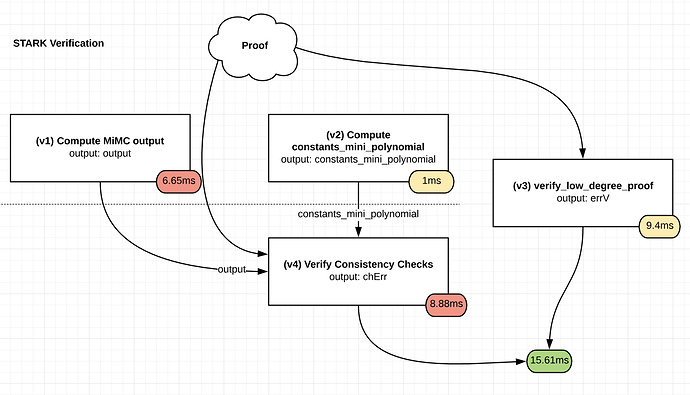
The core is made up of a few hundred rounds of this, and each round only adds a very small number of constraints or arithmetic steps into the SNARK/STARK process because it literally is just a single xor/addition and cubing. In fact, one should be able to literally take the techniques in my STARK tutorial, as written (see the Fibonacci example), make some minor modifications, and make a STARK out of it fairly easily.
Furthermore, one might notice that this primitive can be calculated in the reverse direction, due to Fermat’s Little Theorem or its prime-power-field analogue, but this would take up to a few hundred times longer. However, making a STARK out of the reversed output is still just as easy (you just calculate the STARK of the reverse computation trace). It seems plausible that with some engineering (and perhaps GPU parallelism), the time taken to compute the STARK could be lower than the time taken to run the computation in reverse order, and a possible holy grail would be doing the two in parallel.
What this gives us is a verifiable delay function (ie. a function f(x)=y where y takes some time to calculate that cannot be parallelized away, but (x, y) can be easily verified to be an input/output pair of f) that happens to exactly align with a primitive that is being evaluated for use in hashes, and which hence fulfills the goal of a VDF that only assumes properties of a single cryptographic primitive.
Special thanks to researchers from Stanford, and Zooko Wilcox from Zcash, for pointers and conversations that led to this post.