This is true, but with a good frontend users don’t even need to think about this. Because with the current price of the tokens, we can infer the probability of all events if we assume them to be independent.
I’ll show the case where n=3, with probabilities of events A, B, C being respectively a, b and c. We’ll call t the number of events ending up happening.
The price of Y (“No to all”): y=(1-a)(1-b)(1-c)
Price of A YES: x_A=a(1 - \frac{1}{2}p(t=2|A) -\frac{2}{3}p(t=3|A)) = a (1-\frac{b}{2}-\frac{c}{2}+\frac{b c}{2})
Price of B YES: x_B= b (1-\frac{a}{2}-\frac{c}{2}+\frac{a c}{2})
Price of C YES: x_C= c (1-\frac{b}{2}-\frac{a}{2}+\frac{b a}{2})
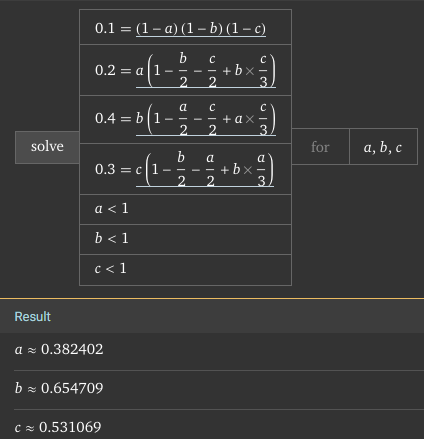
So we have a system of 4 equations with 3 unknowns. I don’t think that there is a closed form equation for it, but a solver should be able to handle it.
I tried on Wolfram alpha with y=0.1,x_A=0.2,x_B=0.4,x_C=0.3 and got the result.
Now, the frontend to make those kind of predictions would work the following way:
Compute the current event probabilities and display those to users.
User picks an event he wants to predict on.
User specifies his predicted probability of the event.
Compute the price of the related token, but this time replacing the probability of the event in question by the user input.
Place an order to buy/sell the related token depending of the computed price.
Continuing with the current example, the front would display:
a: 0.382
b: 0.654
c: 0.531
y: 0.100
The user wants to predict that a is 0.5, we express it by a'=0.5.
So we compute x_A'= a' (1-\frac{b}{2}-\frac{c}{2}+\frac{b c}{2}) = 0.262.
So the frontend proposes to buy tokens of the event A up to a maximum price of 0.262.
The drawback is that there would be some randomness in the user payout (I mean from their perspective, as they’d get an exposure to events they are not knowledgeable about). But if the market is pretty big, the relative variance in term of the number of events happening would be lowered (so the market would actually be less random the larger it is).
I wonder if we could have a prediction market based on this principle. I would see this a bit like the “GMX of prediction markets”.
A potential issue is adverse selection in choosing which events enter the bundle. Adding an event is not neutral: if it resolves true, it increases the number of winning tokens sharing the fixed collateral and therefore reduces every other winner’s payout.
An attacker can exploit this by proposing an event that appears unlikely to everyone else but whose outcome the attacker secretly controls or can strongly influence. The attacker buys its token cheaply while the market still treats the event as improbable, then causes it to resolve true. The attacker receives part of the shared payout while unexpectedly diluting holders of every other winning token. The payout variance is therefore not merely random variance from independent rare events; the outcome-selection process itself can be targeted.
Holding the bundle size fixed, the less likely the legitimate events are, the more cheaply the attacker can acquire a claim that is certain to join an otherwise smaller expected set of winners. The attack therefore captures more of the fixed collateral and imposes a larger haircut on legitimate winners.
Mitigating this requires a curation mechanism that assesses each proposed outcome’s adverse-selection risk and excludes outcomes with plausible hidden influence pathways. Market prices cannot perform this assessment because the attacker trades before revealing either their information or control. Some degree of trust must therefore be placed in the curator’s ability to identify privately controllable outcomes, and in the curator not to act maliciously by intentionally including them.
Indeed, I expect some level of trust that bundle creators wouldn’t do that (can be centralized or a TCR system like curate). I wouldn’t do permissionless bundles.
There may be some level of correlation (like an staking operator being slashed means another one is more likely to be slashed, a rollup hack means another rollup is more likely to be hacked, etc), but I expect the contribution of common causes to failure risks to be lower than the contribution of independent causes. This is indeed a limitation of the system but I think the system would still yield very valuable results.
