One of the challenges with prediction markets on events where the probabilities are very lopsided (ie. either very close to 0 or very close to 1) is that betting on the more likely outcome is very capital inefficient. If the probability of some event is 90%, someone wishing to bet for that event must put up $0.9 of capital per $1 of position, whereas someone betting against the event need only put up $0.1 of capital. This potentially (and arguably already in practice) is leading to prediction markets on such events systematically providing probabilities that are “too far away” from the extremes of 0 and 1.
Arguably, it is very socially valuable to be able to get accurate readings of probabilities for highly improbable events (if an event is highly probable, we’ll think about that event not happening as the improbable event): bad estimates of such events are a very important source of public irrationality. The position “don’t get too worried/excited, things will continue as normal” is often frequently undervalued in real life, and unfortunately because of capital efficiency issues prediction markets make it hard to express this position.
This post introduces a proposal for how to remedy this. Specifically, it is a prediction market design optimized for the specific case where there are N highly improbable events, and we want to make it easy to bet that none of them will happen. The design allows taking a $1 position against each of the N improbable events at a total capital lockup of $1. The design compromises by making the market have somewhat unusual behavior in the case where multiple improbable events happen at the same time; particularly, if one improbable event happens, everyone who bet on that event gets negative exposure to every other event, and so there is no way to win $N on all N events happening at the same time.
The two-event case
We start with a description of the case of two improbable events, a and b. We abuse notation somewhat and use 1-a to refer to the event of a not happening, and similarly 1-b refers to b not happening. Note that you can mentally think of a and b as the probability of each event happening. We consider the “outcome space”, split into four quadrants: ab, a(1-b), (1-a)b and (1-a)(1-b). These quadrants add up to 1:

Now, we will split this outcome space into three tokens: (i) the “yes A” token, (ii) the “yes B” token and (iii) the “no to both” token. The split is as follows:
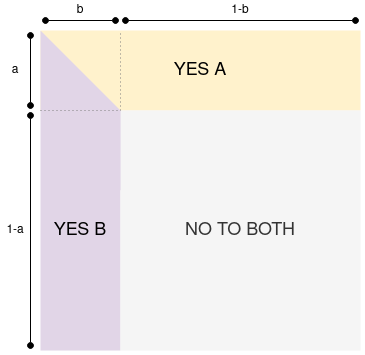
The “no to both” token pays $1 only if neither event happens. If only A happens, the YES A token pays. If only B happens, the YES B token pays. If both events happen, the payment is split 50/50 between the YES A and YES B sides.
Another way to think about it is, assuming the probabilities of the events are a and b:
- The price of the NO TO BOTH token should be (1-a)(1-b)
- The price of the YES A token should be a(1-\frac{b}{2})
- The price of the YES B token should be b(1-\frac{a}{2})
If you expand these expressions, you’ll find that they do in fact sum up to 1 as expected. The goal of the design is that if the probabilities a and b are low, and the events are reasonably close to independent, then it should be okay to mentally just think of the YES A token as representing a (as the \frac{ab}{2} term is very small), and then YES B token as representing b.
Expanding to more than two assets
There is a geometrically and algebraically natural way to expand the design to more than two assets. Algebraically, consider the expression (1-x_1)(1-x_2) ... (1-x_n), claimed by the NO TO ALL token. The YES tokens claim their share of the complement of that expression: 1 - (1-x_1)(1-x_2) ... (1-x_n). This is a sum of 2^n - 1 monomials: x_1 + ... + x_n - x_1x_2 - ... - x_{n-1}x_n + x_1x_2x_3 - ...
Each YES x_i token would simply claim its fair share of all monomials containing x_i: the full share of x_i, half of every x_i x_j, a third of x_i x_j x_k, etc. That is, if only one event x_i happens, the holder of the YES x_i token gets a full $1, but if m events x_i, x_j … x_z all happen, then the holder of each corresponding YES token gets paid \$\frac{1}{m}.
Geometrically, we can see this by extending the outcome space to a hypercube, giving the largest (1-x_1)(1-x_2) ... (1-x_n) sub-hypercube to the “NO TO ALL” token, and then assigning the rest by giving the portion closest to the x_i “face” to x_i. In either interpretation, it’s easy to see how:
- The different shares actually do sum up to $1 (so money does not get leaked in or out of the mechanism)
- The events are treated fairly (no x_i is treated better than some other x_j)
- The mechanism does a good job of giving each YES x_i holder as much exposure to x_i as possible and as little exposure to other events as possible given the constraints.
Extensions
Events with N>2 possibilities (eg. Augur’s “INVALID”)
If there are more than two possibilities for some event, then the easiest extension is to simply treat all possibilities except the dominant as simply being separate events. Particularly, note that if we use the above technique on different improbable outcomes of one event, then it reduces exactly to a simple market that simply has different shares for each possible outcome.
Emergently discovering which side of an event is improbable
Another useful way to extend this mechanism would be to include some way to naturally discover which side of a given event is improbable, so that this information does not need to be provided at market creation time. This is left as future work.