One of the weaknesses of all voting, including quadratic voting, is that for any large-scale issue each individual’s ability to affect the result is so small, and so the incentive to deeply reflect and understand one’s genuine beliefs about an issue is tiny. For example, consider the US election. The probability that your vote will decide an outcome is currently between 1 in 1 million and 1 in 30 billion, with an average of 1 in 60 million. If to you the difference between the two parties for four years is worth $10,000, then your expected value from voting in the election is worth $0.00017. If quadratic voting was used to run the election, we are supposed to believe that people will be willing to spend roughly that amount on voting tokens, and people who care three times strongly really will spend $0.00051 instead, and that people are capable of making such fine-grained value judgements (hmm… is a lottery ticket chance of electing Andrew Yang worth 0.1 penny or 0.2 pennies?).
One possible remedy is sortition, a form of government where instead of polling everyone, you randomly select a smaller subset (“committee”) of participants. Each participant would then have a larger chance of influencing the result, and so would more easily be able to determine what the value is to them of some level of influence on the result, because the influence of each person in the committee would be large enough to notice and reason about on a human scale.
This writeup proposes a combination of sortition with quadratic voting, combining the benefits of quadratic voting and its ability to take into account the strength of preferences with the incentive-concentration benefits of sortition.
Quick quadratic voting overview
In quadratic voting there is a set of participants p_1, \ldots, p_N where participant p_i can make a vote of weight w for a given option on any given issue by paying a cost C(w) = \frac{w^2}{2}. On any issue, the option with the most total vote weight wins.

Here is why quadratic voting is so cool. We can model voters as having a “strength of preference” x, which denotes the amount they are willing to pay for one unit of influence (ie. increasing the weight of their vote by one) on a given issue. A voter with strength of preference x will be willing to continue increasing their weight until the marginal cost of increasing the weight by one unit (ie. the derivative C'(w) = w) exceeds x. Hence, a voter with preference strength x will make a vote of weight x, and so by selecting the option with the highest total weight, the mechanism optimally selects the option with the highest combined strength of its supporters’ preferences. The key realization here is how the cost function C(w) = \frac{w^2}{2} and its derivative c(w) = w naturally incentive-align voters to make a vote whose weight is proportional to how strongly they feel about an issue.
This is better than standard voting, which does not take into account differing strengths of preferences, and is better than fixed-cost-per-vote vote buying, where voters with stronger preferences (or more money) too easily run roughshod over everyone else.
Now, we will try to make modifications of this to add an element of sortition.
Strawman scheme 1
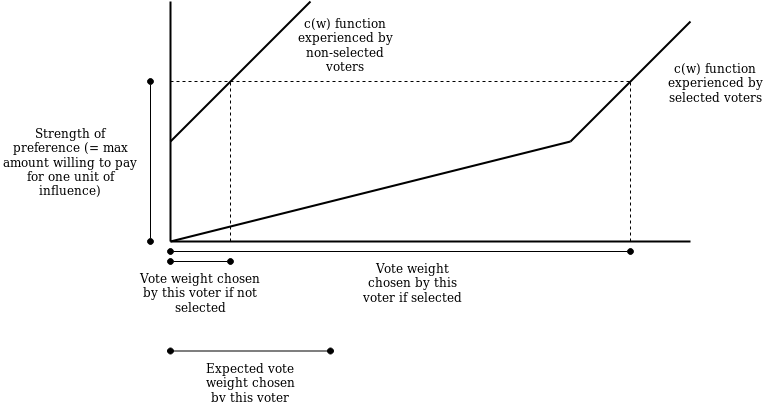
Randomly select portion p of the population. These selected voters have the right to participate in the quadratic vote, and make a vote of weight w with a marginal-cost function c(w) = \frac{w}{p} (remember lowercase c(w) is the marginal cost, the cost of increasing w by an additional unit; C(w) here would be \frac{w^2}{2p}). Everyone else cannot participate.
If you assume that the size of the voter pool is very large, then this modified mechanism will lead to the same result as standard QV: a particular voter with preference strength x will with probability p be able to vote and they will keep voting until c(w) = x, meaning they will make a vote of strength \frac{x}{p}, and with probability 1-p the voter will not be able to do anything. Hence the voter’s expected influence is p * \frac{x}{p} = x.
The main flaw of the scheme is that it does not distinguish between issues are large-scale enough to need sortition (applying sortition to small-scale issues risks adding too much random noise), and particularly it does not deal well with issues where some participants have a really strong position and other participants care little; in those cases, it either applies too much noise to the former, or does not provide sufficient concentration of incentive for the latter.
For a motivating example, consider cases like zoning, where there is typically a concentrated interest (someone looking to build a certain type of property) and an often countervailing diffuse interest (local residents who want to keep their neighborhood a certain way) and it’s not a-priori clear which side should win. We want to make sure the concentrated interest can always express itself but use sortition to amplify the clarity of the diffuse interest.
Scheme 2
We create two voting opportunities. The first voting opportunity allows anyone to buy votes at marginal cost c(w) = M + w for some global constant M (so total cost C(w) = M * w + \frac{w^2}{2}). The second voting opportunity randomly selects portion p of the population, and allows only them to buy votes at cost c(w) = \frac{w}{p} up to a maximum weight of \frac{M}{p}. Note that a selected voter can participate in both voting opportunities.
Now, let’s analyze a voter’s expected influence. With probability p, a voter is “selected”, and in the second voting opportunity they will make a vote of weight \frac{\min(x, M)}{p}; if a voter is not selected they will not vote. In the first voting opportunity, everyone will make a vote of weight \max(x - M, 0). Now, we add these two in-expectation, and we get
p * \frac{\min(x, M)}{p} + \max(x - M, 0) = \min(x, M) + \max(x - M, 0) = x
So this mechanism still gives equivalent results to standard QV in-expectation, and it has the desired property of providing a consistent guarantee of input to strong-preference participants while using sortition to create a portion p of weak-preference participants that have their power amplified by a factor of \frac{1}{p}. But this scheme still feels hacky: you need to agree on both a threshold and a sortition factor for every issue, and it doesn’t seem able to adjust to different levels of preference strength on a finer scale.
Scheme 3
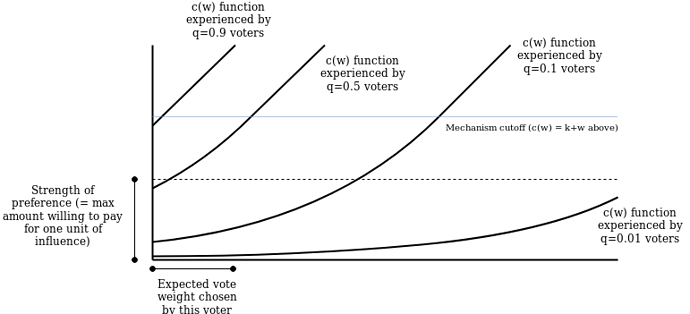
What if instead, we create an infinite sum of schemes of the type presented before, with roughly the following property: above some threshold M, all participants’s votes are counted determinstically, but at level \frac{M}{2} we randomly select half the participants and double their power, at level \frac{M}{50} we select one-fiftieth of participants and 50-tuple their power, etc. This way, the set of participants at any level of preference strength (below the threshold M) that are able to vote have their power amplified to the same level, and so have the same level of incentive to consider the issue well.
Here is the scheme. For each participant, we assign them a uniformly-distributed random value q \in [0, 1]. We give them the ability to vote with a cost function C(w) = M^2 * q * e^{({\frac{w}{M}})} - M * q, so c(w) = M * q * e^{(\frac{w}{M})}. Voters are only able to increase their voting weight up to the point where c(w) = M and no further.
We then as in scheme 2 open a separate voting opportunity to let anyone buy votes at cost c(w) = M + w.
The curve e^{(\frac{w}{M})} has the nice property that scaling it vertically is the same thing as left-shifting it. Hence, instead of treating the multiplication by q as a multiplication, we’ll treat it as voters with lower q values being able to vote along the same c(w) = M * e^{(\frac{w}{M})} curve but starting further left on the curve, where their votes are cheaper and so their power is amplified. Specifically, a voter with preference strength x and value q will buy votes along the curve starting at ln(q) * M (where y = q * M) and ending at ln(\frac{x}{M}) * M (where y = x * M and y' = x).
We can compute the expected vote weight of a voter with preference strength x < M as an integral over q from 0 to \frac{x}{M} (because when q > \frac{x}{M} they won’t vote at all). We cover the M = 1 case first for simplicity of exposition:
And adding back M:
A voter with preference strength x > M will behave as a preference-strength M voter in the first vote, and will make a vote of weight x - M in the second vote as before. Hence, a voter with preference strength x will in-expectation make total votes of weight x.
Also, note that a voter with preference strength x < M, conditional on that voter making nonzero votes, will face q \in [0, \frac{x}{M}] with average q = \frac{x}{2M}, so their average voting weight will be \ln(\frac{x}{M}) * M - \ln(\frac{x}{2M}) * M = \ln(2) * M, so we get the interesting property that any voter below the threshold, conditional on them being able to vote at all, will on average make votes with about the same level of impact.
Further work
- Determine if other sortition functions make more sense
- Come up with principled ways of determining M
- Extend this scheme to quadratic funding (is it as simple as sending the project \sum_i w_i^2?)
For (1), note two ways of describing the problem:
- Give every voter a random uniform-distributed q \in [0,1], and define a set of functions c_q(w) which has the property that \int_{q=0}^1 c^{-1}_q(y) = y where c^{-1}_q is the inverse function of c_q; this follows from the fact that c^{-1}_q(y) = w determines how the weight a voter would vote with if they had preference strength y and a random value q
- All voters can vote using a cost function C(w), but starting from different points (ie. so an individual’s cost function would be C(w) - C(w_i) for some w_i), with the property that if c(w_*) = p (always p \le 1) then the probability any given voter has w_i < w_* is equal to p. Consider different choices for C and how to calculate w_i from q \in [0,1] to be consistent with the criterion.