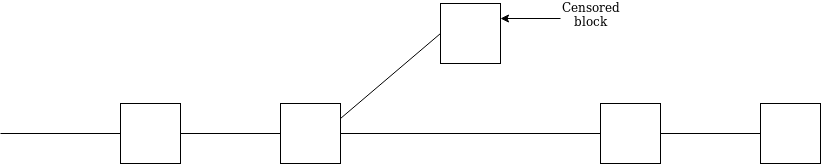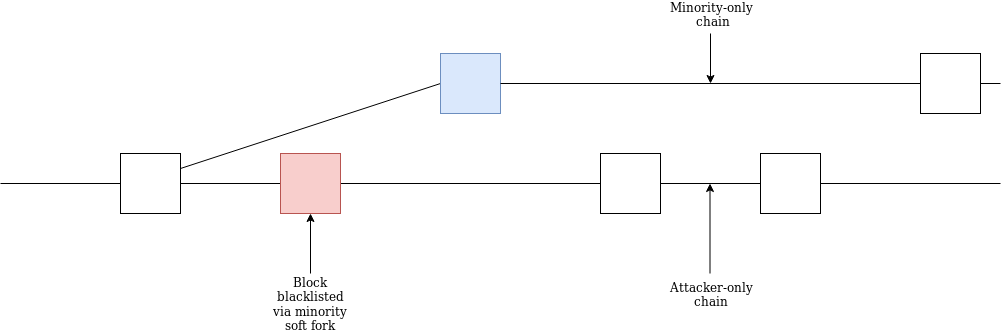The cost of executing a 51% attack on a consensus system, while large, is not infinite, and so the risk that a 51% attack will succeed will always be there. Furthermore, if an attack succeeds, it is very difficult and often impossible to recover from it “within the protocol”. In a proof of work system, a successful 51% attack is profitable, and so funds from that attack could be used to fund the next one ad infinitum, and in ASIC-based proof of work after you buy the hardware once “spawn camping” attacks on the chain are relatively inexpensive. In a proof of stake system, a successful 51% attack could prevent new deposits.
These facts together make it important to have a coherent strategy for how we can respond extra-protocol to a 51% attack to bring the chain back into normal operation. Such a strategy would not be used often; its mere existence may well be enough to deter attacks, but it needs to exist. As we will see, deposit-based PoS is highly secure in part because any kind of 51% attack, even if it requires extra-protocol response, admits a kind of extra-protocol response that causes extremely high economic losses to attackers.
Finality reversion
Finality reversion is by far the most talked-about class of 51% attacks, and in PoS the easiest to handle.
The reason it is easy to handle is that this is the exact situation Casper FFG’s “economic finality” mechanism was designed for: the whole point of BFT finality is that for two conflicting blocks to be finalized, there must be a \ge \frac{1}{3} * |V| sized intersection (|V| being the size of the active validator set) that must have signed two contradictory messages, and so can be slashed - on both chains.
Note that the fork choice rule implemented by clients forbids reverting a finalized block. Hence, if in the above scenario the top chain is finalized before the bottom chain, online clients would all stay on the top chain; only offline clients would see two chains to choose from when they come back online. Offline clients thus would need to reach out to the community (alternatively called “the social layer” or “extra-protocol recovery”) to ask which chain is legitimate. We call this a minor extra-protocol burden: there is a natural correct choice that online nodes agree on, and only a few nodes need to ask what the consensus already is.
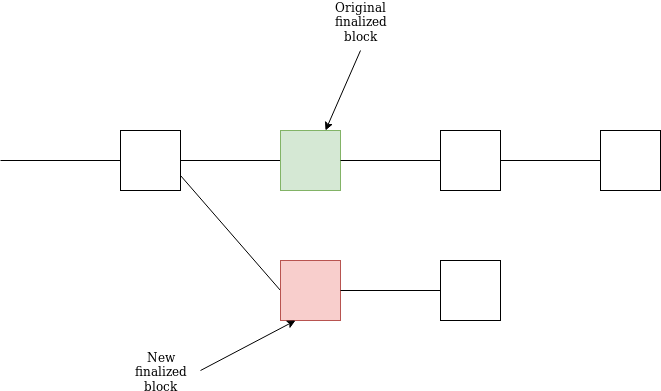
The more difficult case is where two chains are finalized at the same time. Unless the attacker can heavily manipulate the network (certainly a possibility!) a successful attack would take more than \frac{1}{3} * |V|, at least \frac{1}{2} * |V| and possibly even \frac{2}{3} * |V|, making it less likely. Additionally, clients waiting 1 minute after a block is finalized before they show transactions in that block as finalized to users would make this attack much less useful at actually executing double-spend attacks. However, this kind of double-finality attack can still be used to cause chaos.
The simplest approach to recover from this attack would be for users to choose the chain that is supported by the LMD GHOST fork choice rule considering only validators that have not been slashed. However, there is a boundary case where chain A wins the LMD GHOST fork choice rule but chain B was finalized slightly earlier, and it’s not clear which one should dominate.
Hence, an attacker willing and capable of finalizing two chains at the same time can require the community to come together and choose one chain or the other arbitrarily (we can call this a major extra-protocol burden) albeit at very high cost to themselves.
In either case, the attacker is expected to have \ge \frac{1}{3} * |V| validators slashed, which results in penalties amounting in the millions of ether. Hence, the attacker can make finalized transactions break possibly once, and require the community to make a deliberation and users to manually update their clients, but at extremely high cost, which makes it very difficult for such attacks to happen more than extremely rarely.
Validator censorship
Another more difficult kind of attack is the 51% censorship attack. Censorship of transactions is not considered a big issue because we assume that eventually a friendly validator will come along to include any given transaction in a block. Instead, we focus on censorship of validators. Censorship of validators can happen for many reasons; the top two are (i) censoring validators that refuse to cooperate in censoring transactions, and (ii) discouragement attacks.
Censorship is trickier because there are no “slashing conditions” that can detect it: censorship is the act of not including messages that you should have included. In fact, from the point of view of any validator or client that was not online at the time, A censoring B is indistinguishable from B not speaking to A (this is sometimes called speaker-listener fault equivalence). See https://vitalik.ca/general/2017/07/16/triangle_of_harm.html for more writing about this.


However, nodes who are online can detect censorship. The challenge is thus dealing with “boundary conditions”, and determining where to set the line of when censorship is bad enough that extra-protocol intervention, and the challenges of dealing with the boundary conditions that will inevitably arise, are worth it.
Let us distinguish between two cases. First, the censored set is larger than \frac{1}{3} * |V|. That is, somewhere between \frac{1}{2} and \frac{2}{3} of the validators is censoring the other part, and making a chain where those validators cannot get their messages included. Because less than \frac{2}{3} are on the same chain, no blocks are being finalized, and the inactivity leak sets in; on the attacker’s chain, the attacker loses no money (but also gains no rewards), but the victims start losing large fractions of their deposits.
The victims’ only recourse is a “minority soft fork” where they would blacklist the censoring chain and continue working on their own chain. The minority soft fork could be automated: if a chain does not accept your attestations, automatically de-prioritize it in the fork choice, and eventually it will no longer appear dominant.
The attacker would not be able to join both chains, because during each epoch each validator must pick only one chain to participate on or else they get slashed. Eventually, both forks would finalize a block and return to normal, and on the minority chain the attacker would lose a very large portion of their deposits (at least half).
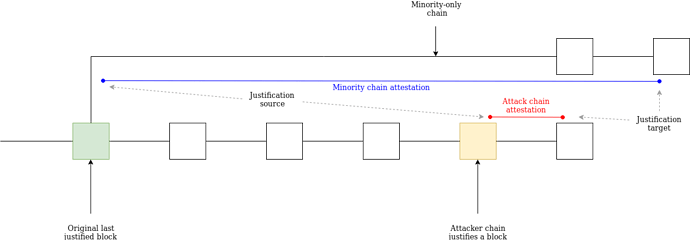
A clever minority could even wait until the attacker’s chain justifies a new block, and the attacker starts building on top of that. The minority could then start building their chain. If they do this, the attacker would not be able to join the minority’s chain without getting slashed by the NO_SURROUND slashing condition:
And if the attacker does not join the minority chain, they lose ~half of their deposits from the inactivity leak.
Now, let’s consider the second case, which is milder. Either the attacker is greater than \frac{2}{3} * |V| and censors the remaining < \frac{1}{3} * |V|, or the attacker carries out the above attack, but in a milder fashion where they allow one every ten blocks to finalize. In this case, there are two solutions. First, one could try to coordinate outside token holders to join and unseat the validator. If the attack chain rejects their deposits, then this fact would be visible to all and would collapse into a scenario identical to the former case. Second, one could still coordinate a minority soft fork, blocking the attacker from joining using the technique above.
Note that both of these techniques rely on some form of coordination between an honest minority to determine what a blacklist-worthy chain is. One could simply count on the social layer to do this; even the possibility of the social layer making a determination that is unfavorable to the attacker will make attacks in expectation expensive.
However, one could conceivably create tools to assist coordination. A simple one is the 99%-fault-tolerant consensus gadget proposed here: https://vitalik.ca/general/2018/08/07/99_fault_tolerant.html, which could create consensus among online nodes with reasonably low network latency that a message actually was published in a given epoch, and so if that message is not included in the next epoch something is going wrong.
Summary
In the case of a finality-reversion attack, we already know that the attacker can get slashed and so the attack can be very costly (think: millions of ETH). Attacks that try to muddy the waters of which block came first, so as to make extra-protocol coordination on which chain to continue with after the attack, are even more costly. Censorship attacks are more challenging in that, absent social responses, they succeed and cause harm “by default”, though clients can implement features that reject chains that seem to censor too much, and such attacks can be defeated by extra-protocol consensus on a “minority soft fork” that cleverly uses the NO_SURROUND slashing condition to focus on a chain that the attacker cannot legally join.
In either case, a 51% attack would be a moment of joy for the community, as at the cost of a day or perhaps a week’s disruption, an amount of the attacker’s ETH would get burned that counteracts years of protocol-level issuance, increasing the value of ETH and hence making future attacks more expensive. Furthermore, this can be done via soft forks or fork choice rule features, with no need for hard forks that take the attacker’s coins out manually.