Sharded Byzantine Atomic Commit

Sharding
1

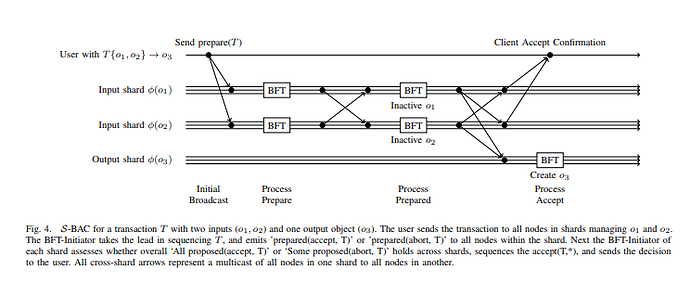
I’ve just read up on Ethereum’s sharding documents (and am currently reading all the threads here), and hope to contribute some ideas. Given the recent threads on cross-shard locking schemes, I thought it would be a good time to jump in.

I’d like to introduce Sharded Byzantine Atomic Commit (S-BAC), a correct inter-shard consensus algorithm for atomic commitment. Unlike previously proposed algorithms, S-BAC does not rely on the client being honest to guarantee liveness, and thus no lock time-out period for clients is required to prevent deadlocks. The liveness property depends on shards being honest.

For the full details and security proofs, see page 7 of our Chainspace paper.

Here is an overview of the protocol:

image
image744×306 35.6 KB

The protocol is agnostic to the actual BFT protocol algorithm used - that is, it doesn’t matter if you use PBFT or a blockchain + proof-of-work/proof-of-stake. For the evaluation of the protocol in the paper, we used PBFT.

There are some optimisations that can be made when using a blockchain + proof-of-work/proof-of-stake, however. For example, if a shard includes a prepared(accept, T) message on the blockchain for a transaction T, but T eventually gets aborted, then that can be considered to be a waste of space on the blockchain. In another post, I will propose a way to safely and permanently prune such messages from the blockchain, even from archival nodes, so that they are not needed to bootstrap a full node.

2 Likes
2

Hey, nice work Musalbas! Can you please say a few words to give the intuition of how your system works? Seems from the diagram that you are using pBFT to agree on cross shard transactions, but for transactions that take place within a single shard I guess the pBFT mechanism is not necessary. How will this system scale if many transactions are cross shard and thereby must be shared with all other shard members?

3

Mustafa - so judging from the picture this would require n^2 messages where n is the number of shards, since each shard sends messages to each other shard.

Why would not you use one shard as a leader if all shards are good anyway :-)) Then it would be n

1 Like
4

See page 7 of the paper. It works similarly to a two-phase commit. We’re not using PBFT in the diagram; any BFT protocol works (e.g. blockchain + proof-of-work). The prototype uses PBFT. For single-shard transactions technically you don’t need the two-phase commit, you can just commit the transaction in one phase.

The more shards each transaction touches, the lower the throughput, as once you have a situation where all transactions touch all shards, that’s effectively equivalent to having a non-sharded blockchain. Here’s a graph:

image

I think you could as if any shard that a transaction touches is dishonest, then liveness is compromised. However, if the leader shard is dishonest, then that further allows them to potentially frame other shards as being byzantine, by not relaying their messages, to block transactions from progressing.

5

I think we could combine your work and mine so shards request locks, ensuring liveness, but not all locks need be acquired in a given round.

6

so，is there a related solution to optimize it?

7

It’s not really a problem, but a natural property of sharding. If you want to make a transaction that modifies state in multiple shards, all of those shards have to be involved in some way, you physically can’t do better than that.

1 Like
8

a good allegory, thank you ~