TLDR
- Slot inclusion rate, the number of slots required for a blob to be included in the beacon chain, has a high variance and is higher for some rollups than others.
- The current combinatorics of the blob market has an integer packing problem. This is a type of combinatorial optimization that generally involves packing objects of different sizes into a finite number of containers or bins.
- Data suggests that the integer packing problem is contributing more to higher slot inclusion rates than builder censorship.
Introduction
This post offers a fresh perspective on the current design and constraints of the blob market, presenting additional data (from a blob tracking dashboard created at Primev) on slot inclusion concerning reorg risks, and a combinatorial analysis of the blob market design, revealing an integer packing problem.
The key metric in this post is the slot inclusion rate. The slot inclusion rate indicates the number of slots required for a blob to be included in the beacon chain,
with a higher rate signifying a longer inclusion time.
Recent research on the blob market [1], [2], [3] has focused on how larger blobs increase reorg risk due to higher latency. This could incentivize builder censorship to reduce latency by excluding blobs from blocks.
Despite the blob market being under capacity and the base fee remaining at 1 wei, research [4] shows that rollups like Optimism and Base often have high slot inclusion rates, taking more than five slots to be included. Given the underutilized market, this seems counterintuitive, suggesting possible latency censorship. However, the current blob submission strategies and blob market combinatorics suggest that higher slot inclusion rates may indicate increased competition between blob producers rather than builder censorship.
Blob Submission Strategies
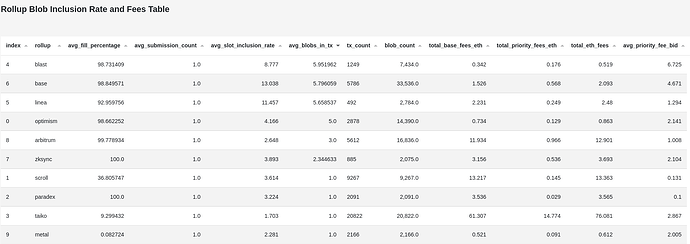
The below table from the dashboard shows a 7 day snapshot of the largest blob market participants.
There are now 3 major strategies across the number of blobs:
- submit the max 5-6 blobs at a time (blast, base, linea, optimism)
- submit 3-4 blobs at a time (arbitrum, zksync)
- submit 1-2 blobs at a time (taiko, metal, paradex, scroll)
Aggregating blobs into fewer transactions reduces transaction expenses (base fee, blob fee, priority fee) but increases slot inclusion times. In contrast, smaller blob transactions improve slot inclusion times at the cost of higher transaction expenses.
Slot Inclusion Rates
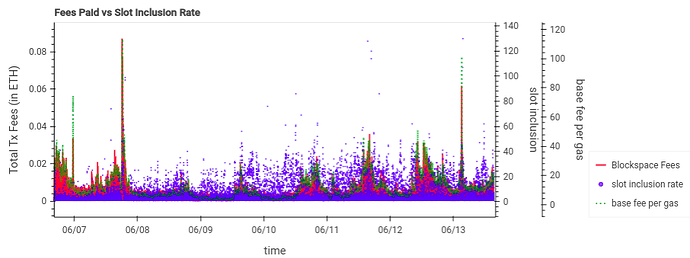
The next chart displays a time series overlay of base block demand (total transaction fees and base fee in gwei) with the slot inclusion rate for each blob transaction. It shows high slot inclusion rates, up to 30 slots, even during periods of low blockspace demand.
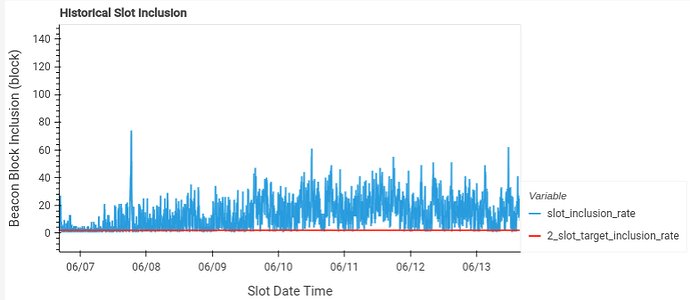
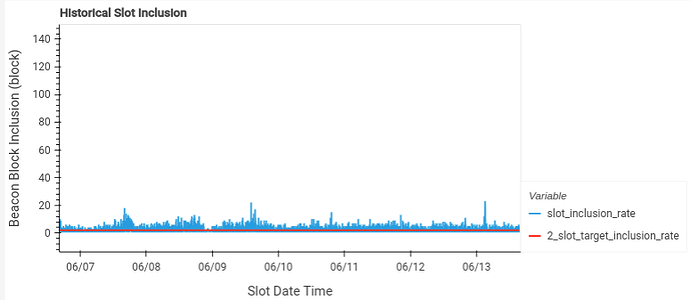
The table mentioned earlier above contains the average slot inclusion rate for each rollup. Base, which submits the largest blobs in each transaction has the highest, averaging 13 slots. Taiko has the lowest average at 1.7 slots and submits only single blobs for each transaction right now.
Base slot inclusion rate:
taiko slot inclusion rate
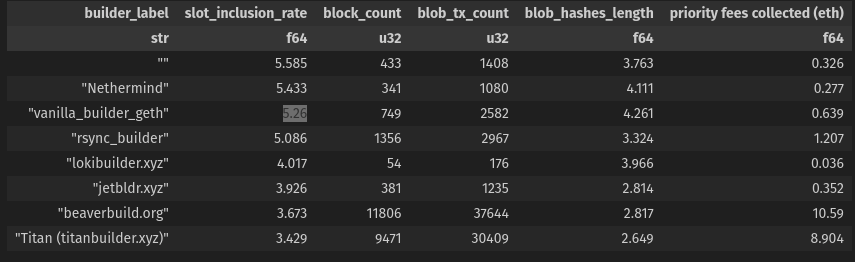
Builder Slot Inclusion Rates
This table examines slot inclusion rates from the builder’s perspective, including the number of blocks, blob transactions, average blob count, and priority fees collected.
A higher slot inclusion rate means a blob has waited longer to be included in a block. An efficiency metric would be to have the lowest possible slot inclusion rate, indicating that builders are including blobs sooner rather than later.
Builders like Titan and Beaverbuild have more efficient blob slot inclusion rates than vanilla builders. They also have the lowest average blobs per block. This could be due to their efficiency in accepting strategies like Taiko blobs over other block builders.
Combinatorics
This notebook uses dynamic programming to count the number of combinations of blobs for the current blob market. Given the current 6 blob per block capacity and 6 blobs per block, there are 11 possible combinations.
Occurrences of each number:
1: 19
2: 8
3: 4
4: 2
5: 1
6: 1
A trivial observation is that there is only one combination in which a block can fit 5 or 6 blobs. Since 4 out of 10 rollups submit these 5 and 6 blob transactions, there will only be one winner. Additionally, a single 1-blob transaction can “censor” a 6-blob transaction for an entire slot by being accepted first.
The combinatorics of the current blob market size suggest that the small size itself is causing higher slot inclusion problems, rather than blob censorship latency. This indicates that censorship is not from builders but from competition among blob users.
This raises an important question: what is the optimal maximum number of blobs allowed in a block relative to the maximum number that can fit in a block? Would the combinatorics be more favorable if the maximum blob size were 3 instead of 6? Would it be better to allow 9 blobs per block instead of 8? There is an economic incentive to group blobs as large as possible to save on costs, which disproportionately favors larger rollups over smaller ones until blob sharing becomes feasible.
Bidding Strategies
Currently, blobs use static bidding strategies, generally resubmitting their blobs if their bids sit in the mempool for too long. This shows a certain level of insensitivity to slot inclusion for each rollup. If a blob is delayed for 100 slots, there seem to be no consequences or incentives to increase slot inclusion rates at this time.
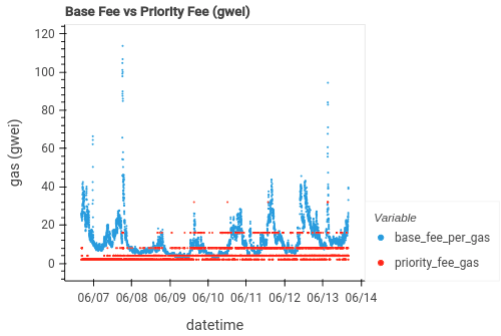
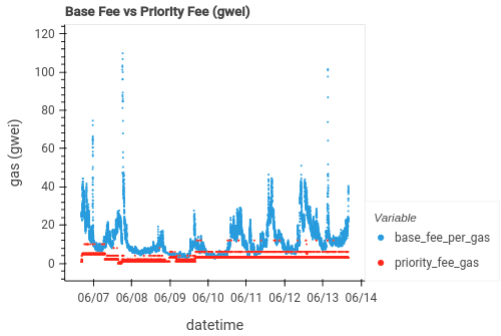
The two charts below show sample bidding strategies used by Base and Taiko, just two examples of the rollup strategies available on the dashboard. Base averages a priority fee of 4.5 gwei, while Taiko averages 2.9 gwei. There is no correlation between priority bids and base fee fluctuations.
base:
taiko:
Resubmitting blobs through the mempool is expensive and generally not recommended as a good practice. This creates the problem of how blob producers can become more competitive in their bidding strategies if they need to make their slot inclusion rates more efficient.
One solution is to use preconfirmations. For example, using a protocol such as mev-commit to attach preconf bids to blob transactions would allow rollups to dynamically adjust their bids without having to resubmit blobs into the mempool. A stronger solution would be to receive preconfirmations from proposers to guarantee that builders wouldn’t be able to censor blobs.
Conclusion
Analysis of slot inclusion rates and blob market combinatorics reveals a complex interplay between efficient slot inclusion, competition, and potential censorship. While current data suggests that high slot inclusion rates are primarily driven by competition among blob users, there remain several unanswered questions:
- What is the optimal maximum number of blobs per block to balance efficiency and fairness?
- How can blob producers develop more competitive bidding strategies?
- Could the implementation of dynamic bidding strategies or preconfirmations significantly reduce slot inclusion times?
- What long-term effects might increased competition and potential latency censorship have on the blob market?
The combinatorics of the blob market are a fundamental factor affecting slot inclusion efficiency and cost. By understanding and optimizing these combinatorial constraints, it is possible to enhance market dynamics, reduce costs, and improve transaction efficiency for all participants. Further research and experimentation are needed to address these questions and optimize the blob market for all participants.