I understand that the FRI proof does not guarantee that all values are one the same low-degree polynomial, but I think that if you sample in a systematic way it is guaranteed that the values that are sampled and verified have to be on the same low-degree polynomial.
I hope I can explain what I mean.
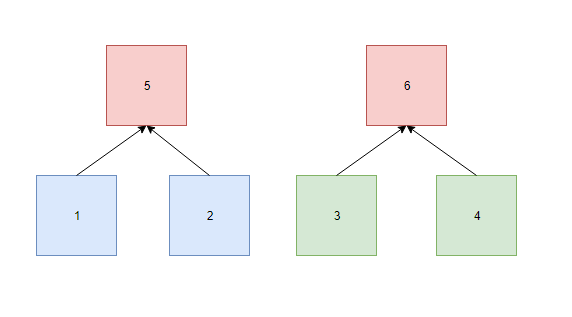
Lets start with the simplest FRI where there are just two values in the block as depicted in the below graph.
We start with the two blue values in boxes 1 and 2. These values are expanded (Reed-Solomon) into the two green boxes 3 and 4. So these four values are on the same low-degree polynomial (D<2)
We build a Merkle tree based on these four values and pick a column based on the root of the Merkle tree. Boxes 1 and 2 are on the same row, so we combine these values and calculate the column value and put this in box 5. We do the same for Boxes 3 and 4 and put the column values in box 6.
The values in Boxes 5 and 6 are now on a polynomial of D<1, so have to be equal. We put these two values in a separate Merkle tree.
The roots of both Merkle trees are send with the block header (or a Merkle tree of the roots).
Light-client A samples the values in boxes 1,2,5 and 6 and checks whether the values are correct.
Light-client B samples the values in boxes 3,4,5 and 6 and checks whether the values are correct.
My claim is that if both light-clients can verify the values they have sampled, they can be sure that the values in boxes 1,2,3 and 4 are on the same low-degree polynomial (D<2).
I believe this to be the case, because the only way you can chose the values in box 3 and 4 to be sure that (regardless of the picked column) the values in boxes 5 and 6 will be the same is to make sure the values in boxes 1,2,3 and 4 are on the same line. If you chose any other values, the chance that the values in box 5 and 6 are the same are extremely small.
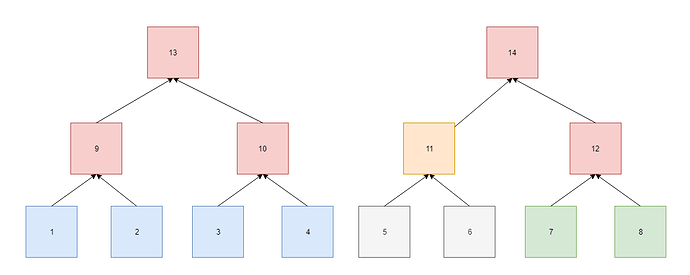
Now look at an example with four values as depicted in the graph below.
Now we start with four values and expand these to eight values that have to be on a polynomial of D<4. We generate the Merke tree of these values and pick a column based on the root. With this column we calculate the values in boxes 9,10,11 and 12 that have to be on a polynomial of D<2. Via the Merkle root of these four values we pick a new column and calculate the values in boxes 13 and 14. The values in these two boxes have to be on a polynomial of D<1, so these values have to be the same.
Light-client A samples the values in boxes 1,2,3,4,9,10,13 and 14 and checks whether the values are correct.
Light-client B samples the values in boxes 7,8,11,12,13 and 14 and checks whether the values are correct.
My claim is that if both light-clients can verify the values they have sampled, that they can be sure that the values in boxes 1,2,3,4,7 and 8 are on the same low-degree polynomial (D<4).
We have already seen that the values in box 11 and 12 have to be on the same low degree polynomial (D<2) as the values in boxes 9 and 10 to make sure the values in boxes 13 and 14 are the same.
The only way you can chose the values in boxes 7 and 8 and make sure that the value in box 12 is correct (regardless of the picked column) is to make sure these values are on the same low-degree polynomial as the values in boxes 1,2,3 and 4. If you chose any other value, the chance that the value in box 12 is correct is extremely small.
To summarize: my claim is that as long as a light-client samples and checks all boxes above the sampled bottom-layer values, the bottom-layer values are guaranteed to be on the same low-degree polynomial.