SubnetDAS - an intermediate DAS approach

[fradamt]

@djrtwo

validators – or nodes-with-validators attached? I’m assuming the latter given the target values. You could try to enforce that all validators download/custody r. This is nice that it scales responsibility with # of validators, but it ends up not really being enforceable wrt purely p2p perspective. But it is natural to then roll that into a crypto-economically enforceable scheme with proof-of-custody.

I was thinking the former, i.e., a per-validator custody assignment

@djrtwo

Are extensions sent in the row subnets? or should just the entire Blob payload be dropped in and sent contiguously? In 4844, we send entire blobs (rather than streaming points), I could imagine on these row subnets to just do the same and forwarding validity condition is just that the blob is fully there and correct. Potentially lose some p2p parallelization/streaming optimizations though

Another thing to consider in the event of sending individual points on subnets is anti-dos/validity conditions. If you already have the block, then you can check validity before forwarding, but if you don’t necessarily (e.g. like the 4844 decoupling), then you need proposer signatures over each point (or whatever amount the data is bundled) for some amount of anti-dos.

I think it would be preferable to gossip blobs in the row subnets, rather than extended blobs, just to save on bandwidth. Nodes can re-do the extension locally.

For local reconstruction, it would be necessary to allow gossiping of individual points (here meaning a cell, the intersection of a row and a column, which would be 4 field elements with the example parameters) in row subnets. For this, I think it would be ok to wait to have the block (or at least a header and the commitments, if they were to be gossiped separately) so that you can validate whether or not you should forward.

@djrtwo

What does a node do to “catch up” on prior slots that they cannot follow live via gossip? I assume you need some sort of req/resp interface for querying this data up to the pruning period (similar interface to PeerDAS). If that’s the case, you almost support PeerDAS “for free” when implementing SubnetDAS.

For column subnets, I think it would be ok to just choose k subnets, join them and request historical samples from them, regardless of whether there is supposed to be some subnet rotation when you’re doing sampling “live”. For row subnets, I think in the latter case (e.g. if as a validator you are meant to be in 1 stable row subnet and in 1 which rotates) you probably want to join one row subnet at a time, out of the rotating ones which you have been assigned to in the period you couldn’t follow live, and request all blobs you need from that subnet. Basically catching up subnet by subnet instead of slot by slot, so you don’t have to keep hopping between subnets.

Either way yes, I think the kind of req/resp interface mentioned in PeerDAS seems like the right tool here, and I guess peer sampling would be supported as long the same interface can also be used without being in the same subnet. think that supporting peer sampling would be great, because, as I mentioned in the “Why SubnetDAS” section, it could (potentially optionally) be used only as part of a confirmation rule, which I think retains all its added security value while preventing any negative effect on the liveness of the network.

@djrtwo

right, but if the honest majority assumption fails, then with linkability some nodes could be tricked to confirm unavailable data, whereas this is not the case with unlinkability. So it’s not that you are making different assumptions, it’s that when comparing linkability and unlinkability as a paradigm within DAS, the extent to which you break under the failure of that assumption fails.

It’s true that, when the honest majority assumption fails, unlinkability still prevents any full node from seeing an unavailable chain as canonical. What I am questioning is whether or not this is actually very useful. For the safety of rollups, I don’t think this is very important at all, because anyway it’s hard to imagine that the canonical Ethereum chain could end up being one which only a small minority of full nodes see as available. I also don’t think we should rely on query unlinkability for the safety of rollups, unless there’s a bulletproof way to achieve it, which is not so clear, so I think that the “honest minority of full nodes” argument is anyway the best defense we have there.
For the synchronous confirmation rule, a malicious majority can cause reorgs, and thus safety failures for full nodes which use that rule, regardless of whether queries are linkable or not. If a full node confirms chain A and then reorgs to chain B, unlinkability still guarantees that chain A was available. But why does it matter whether it was? It seems to me that the safety violation due to the reorg is what matters here.

@djrtwo

Does this number – 10% can be fraudulently convinced – significantly change at lower data throughputs (e.g. 1/4 or 1/8 of the full amount) or do any other considerations of the analysis change in meaningful ways?

If the throughput (number of blobs) is reduced by a factor of x without changing anything else, then the security is exactly the same, we just decrease the bandwidth requirements by x as well, because samples (columns) are x times smaller. Of course one could allocate part of the throughput decrease to lowering requirements and part of it to boosting security.
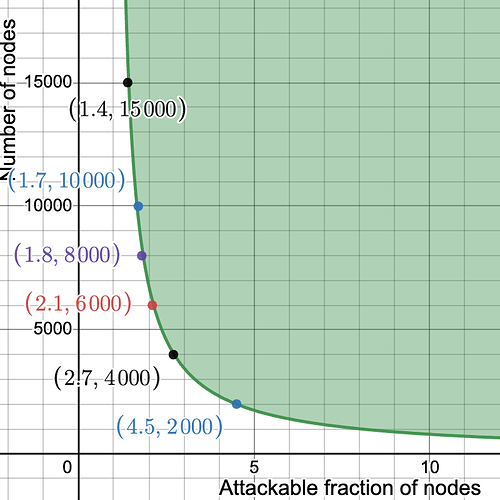
For instance, with 1/4 of the throughput one could double the number of samples while still halving the bandwidth requirements. This is the full graph for the resulting security, with k=32, m = 2048. Even with 2000 nodes, the attackable fraction is below 5%.

@djrtwo

You mention “blobs, # of samples to download, security” as the trade-off space. Is this complete or are there other factors? I suppose security catches other concepts than just how-many-nodes-can-be-fooled – such as how populated subnets are wrt node count.

Yes, subnet population is also part of the trade-off space.
With b = \text{number of blobs}, n = \text{number of nodes}, s = \text{blob size}, we have these:

Throughput: s * b
Bandwidth per node: k/m*(2*\text{throughput}) = 2sb*k/m
Subnet population: k/m*n

k/m is both the percentage of the extended data which is downloaded by each full node and the percentage of full nodes which are in each column subnet, so, for fixed n, we can’t increase subnet population without equally increasing bandwidth per node.

For fixed n and s, the levers we have are basically:

• Increase b, which proportionally increases throughput and bandwidth requirements and leaves everything else unchanged
• Increase k, which increases safety and proportionally increases bandwidth per node and subnet population
• Increase m, which decreases safety and proportionally decreases bandwidth per node and subnet population

(Here safety = how-many-nodes-can-be-fooled)

Given a maximum bandwidth per node and minimum subnet population, we can get the maximum supported throughput. The only wiggle room we have is that we can increase safety by increasing k and m while keeping k/m fixed (increasing k has more of a positive effect than the negative effect of increasing m).

Something that is not clear to me here is what are the effects of increasing m while keeping k/m fixed. With 10000 nodes, how does having 100 subnets where each node joins 1 (100 nodes per subnet) compare to having 1000 subnets where each node joins 10 (also 100 nodes per subnet)? Is there significantly more overhead (or some other notable problem) in the second case?

Also not clear to me, what is the impact of the number of nodes? Do we care about the absolute number of nodes per subnet (k/m * n) or the relative one (k/m)? In other words, does having more nodes overall mean that we can increase throughput without making anything worse, or do we anyway always need to keep k/m somewhat high?

@djrtwo

Can you explain more about if/where a 2D encoding can fit into this scheme?

The issue with a 2D encoding in this context is that the number of subnets is the number of samples, and this would be very high if we use points as samples, e.g. with a 256x256 square (128 blobs, vertically extended, split into equally sized columns) we’d get 64k samples/subnets. We could do the 2D extension but still use thin columns as samples, but then I am not sure there is any benefit, and we still double the amount of data?

A reason to do a 2D encoding could be if we want to also support a cheaper kind of sampling, with much smaller samples, e.g. columns are used as samples by SubnetDAS, so the number of subnets is still low, but points are used as samples by PeerDAS. Although even in this case, I don’t see why we couldn’t just use even thinner columns as samples for PeerDAS? For example, here the red columns still correspond to subnets, are used for distribution and for subnetDAS, and are somewhat large because we don’t want too many subnets. They can then further be broken down into thinner green columns, which are used by some other lighter form of DAS that does not use subnets.

@djrtwo

Do you have any intuition or analysis on what the options are for a node that does miss a single sample? Can they increase the amount of samples they are querying with an acceptable miss rate?

For example, one could tolerate a single miss out of the k queries. That would make the failure probability for each node \binom{k}{0}2^{-k} +\binom{k}{1}2^{-k} = (k+1)2^{-k}, and the failure probability for n\epsilon nodes ((k+1)2^{-k})^{n\epsilon}, adding a factor of (k+1)^{n\epsilon} compared to the analysis from the post. The expression we care about then becomes: \ (n+m\ +\ \log_{2}\left(k+1\right)n\epsilon\ -kn\epsilon)-\log_{2}\left(e\right)\frac{n\left(1\ -\ 2\epsilon\right)^{2}}{2}-\log_{2}(\sqrt{nm}\frac{\pi}{2}) - 30, with (\log_{2}\left(k+1\right)-k)n\epsilon instead of just -kn\epsilon. To get the same security as before, we then need to increase k roughly by \Delta k = \log_{2}{k}, e.g. we get roughly the same security with k=16 and no tolerance for misses or k=20 and tolerating a single miss. You can check this out here.

Playing around with the parameters, it’s pretty clear that tolerating multiple misses is not really practical, because it ends up requiring a significant number of additional samples. This is because, to tolerate t misses, the failure probability for a node blows up to \sum_{i=0}^{t}\binom{k}{i}2^{-k}.