Background
This blog post describes our implementation of legendre PRF based “Proof of Custody” using HoneyBadgerMPC framework. The link to the codebase along with the instructions can be found here. In short, Proof of Custody is a way for nodes (called validators) to “prove” that they are really storing a file which they are obligated to store. Prior realizations of this scheme utilized a “mix” function based on SHA256. A future goal is to make use of primitives which allow: i)validator pools to be set up in a secure, trustless manner, (ii) allow one-party validators to spread their secret across several machines, reducing the risk of secrets getting compromised. In order to meet this goal, it is required that the primitive is MPC-friendly which, unfortunately, is not a property of SHA256. Fortunately, the “mix” function in the Proof of Custody scheme can be replaced with any PRF. Consequently, it was proposed that Legendre PRF, an MPC-friendly primitive, would be a good candidate for such replacement. See this post (Using the Legendre symbol as a PRF for the Proof of Custody) for a detailed backgound.
Setting
There are n nodes out of which t might be malicious. Additionaly, there is a secret-key K which is secret-shared among the n nodes using a (t, n) threshold secret-sharing scheme. This means that atleast a group of t+1 nodes are required in-order to reconstruct the secret-key K. In order to “prove the custody” of a file represented as a set of B blocks - {X_1, X_2, .... X_B} - which is basically a public dataset of B field elements, the nodes compute the output of legendre PRF function using their secret key share [K] and the B field elements as input. This output is represented in the following equation:
where
Once each node has computed its share of the output, those outputs can be combined to reconstruct the actual output. In a setting where n > 3t, we can use a technique called robust interpolation for such reconstruction. This technique ensures that: i) reconstructed output always matches with the expected output, ii) nodes which did not submit or submitted incorrect shares of their PRF output are always identified. This identification of malicious behaviour (coupled with a scheme which provides rewards to nodes who submit correct output shares) incentivizes the nodes to perform the MPC computation honestly.
Protocol
Below, we outline the protocol that each node follows:
Precompute:
- [K],[K^2],...[K^B] : powers of secret-share of key for each block
Online computation:
- Compute [y] where y = (K+X_1)(K+X_2)....(K+X_B) through local computations. This is a polynomial y = f(K) where the coefficients of f can be determined from constants X_1,...,X_B and we have powers of [K] precomputed
- Compute [F_K(X)] := [y]^{(p-1)/2} through log_2 p multiply/squarings
- Open [F_K(X)] and reconstruct to obtain F_K(X)
Implementation
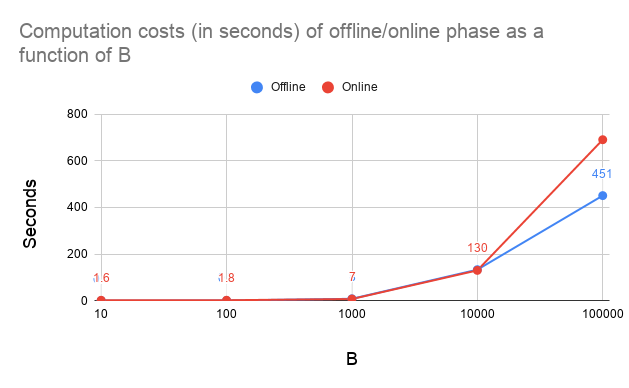
We have implemented the above scheme using HoneyBadgerMPC framework. HoneyBadgerMPC is unique in that it focuses on robustness. In a network of n server nodes, assuming at most t<n/3 are compromised, then HoneyBadgerMPC provides confidentiality, integrity, and availability guarantees. In MPC terminology, it is asynchronous, provides active security, has linear communication overhead, and guarantees output delivery. Other MPC toolkits, such as SCALE-MAMBA, Viff, EMP, SPDZ, and others, do not provide guaranteed output delivery, and so if even a single node crashes they stop providing output at all.The link to the codebase along with the instructions can be found here. In our code, the above protocol is implemented inside the prog() in 2 different phases:
-
Offline Phase : In this phase, each node obtains a (t,n) secret-sharing of key K, and then each node computes successive powers of their secret share ([K], [K^2], [K^3], etc) using the
offline_powers_generation()function -
Online Phase : In this phase, nodes run a MPC protocol using the public file (represented as an array X of B elements) and the preprocessed powers of secret shared key as input. The logic for same is present in the
eval()function. The output of this function is a secret-sharingfk_xof the desired output. After this, each node reconstructs the desired outputFK_xusing theopen()function.
Difference between our implementation and a real-world deployment
Our implementation differs from a real-world deployment in the following ways:
1.) The nodes in our implementation are “simulated” as async tasks which execute concurrently on the same system and communicate with each other using message passing. However, in the real-world, each node would correspond to a validator (a standalone system) and the communication would happen over network sockets.
2.) In our implementation, nodes obtain a share of the predetermined secret-key K which is computed by the HoneyBadgerMPC system. In the real world, the “one-party validator” node will be holding the secret-key K and will be responsible for distributing shares of it to each of the n nodes in the “validator pool”
Acknowledgements
As already mentioned, our implementation makes use of HoneyBadgerMPC framework which has been developed under the supervision of Andrew Miller and others. I am a first year PhD student working under Andrew Miller at Decentralized Systems Lab, UIUC. You can find out more about me here