For background see: Rate-limiting entry/exits, not withdrawals
We can calculate the safety of a block taking into account the passage of time as follows. Suppose that the last finalized block you saw was at time T_0, the current time is T_{now}, and you receive a finalized block from slot T_L (call the older block B_0 and the new one B_L). ("from slot T" means "supposed to have been published at time T") How many validators would need to be slashed for the network to have accepted some block B_R conflicting with B_L as final?
If the validator set is static, with N validators, then the answer is obvious: \frac{N}{3}. But what if the validator set can change, and specifically if N validators are part of the validator set of a block at slot T then the validator set at slot T+1 can incur a maximum of a(N) activations and e(N) exits?
We know the number of activations and exits between the validator set of B_0 and that of B_L exactly; call this a_L and e_L. We can also compute an upper bound on the number of activations and exits between B_0 and a hypothetical block B_R that appears now; we can call this a_R and e_R. If the activation and exit rates are constant, then a_R \le k_1 * (T_{now} - T_0) and e_R \le k_2 * (T_{now} - T_0). If the rates are proportional to validator set size, then A_R = |V(B_0)| * (e^{\frac{T_{now} - T_0}{k_1}} - 1) and e_R = |V(B_0)| * (e^{\frac{T_{now} - T_0}{k_2}} - 1). If the formula is more complex, the calculation will be more complicated.
Now, we can calculate the intersection of quorums of B_L and B_R. Here is a Venn diagram to illustrate what is going on:
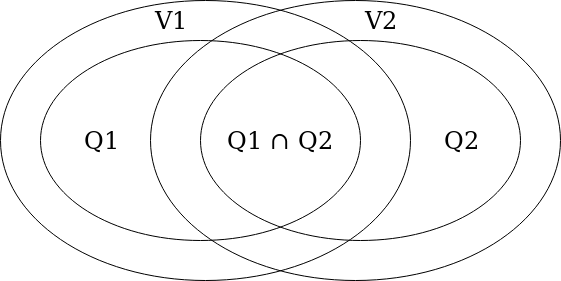
The validator sets of B_L and B_R are V_1 and V_2. The validator subsets that participated in finalizing each block (“quorums”) are Q_1 and Q_2, with |Q_i| \ge \frac{2}{3} * |V_i|. The intersection Q_1 \cap Q_2 gets slashed.
The size of the set complement V_2 - V_1 is a_R + e_L, and V_1 - V_2 is a_L + e_R. Let I = V_1 \cap V_2 (“intersection”). In the worst case, members of these complements are all members of Q_1 or Q_2, so |Q_1 \cap I| \ge |V_1| * \frac{2}{3} - a_L - e_R and Q_2 \cap I \ge |V_2| * \frac{2}{3} - e_L - a_R. We also know I equals |V_2| - a_R - e_L or |V_1| - a_L - e_R. To do a sneaky mathematical trick, we’ll use the affine-combined form (|V_2| - a_R - e_L) * \frac{2}{3} + (|V_1| - a_L - e_R) * \frac{1}{3}.
We can compute the intersection that gets slashed via |Q_1 \cap I| + |Q_2 \cap I| - |I| or:
|V_1| * \frac{2}{3} - a_L - e_R + |V_2| * \frac{2}{3} - e_L - a_R - |V_2| * \frac{2}{3} + a_R * \frac{2}{3} + e_L * \frac{2}{3} - |V_1| * \frac{1}{3} + a_L * \frac{1}{3} + e_R * \frac{1}{3}
This simplifies to:
|V_1| * \frac{1}{3} - a_L * \frac{2}{3} - e_R * \frac{2}{3} - e_L * \frac{1}{3} - a_R * \frac{1}{3}
If our goal is to take into account latency until validators get slashed, then we would need to add another parameter \delta and compute the “escapees” on each chain via k_1 * \delta, |V(B)| * (e^{\frac{\delta}{k_1}} - 1) or otherwise the appropriate formula to count exits, and subtract the escapees from the intersection to determine how many validators must have been slashed on each chain.
Implementation
Whenever a validator receives a new block, they know the previous finalized block that they saw, B_0, as well as the new block B_L and the upper bound on time T_{now}, so they can simply use the formulas above to compute the actual safety level of the block.