A short note on Post Quantum Verkle explorations

[CPerezz]

A short note on PQ-Verkle

I want to thank @gballet and @ihagopian for helping me understand all Verkle Tree’s tradeoffs and resolving all my doubts. Also @arantxazapico and @WizardOfMenlo for good discussions and help towards understanding the SoTA of lattice-based vector commitments.

While revisiting EIP6800 (Unified Verkle Tree as ethereum’s state structure) I asked myself the following questions:

• What problem are we actually addressing?
• What properties did we actually like from Verkle?
• Would Verkle be the best solution in a non-PQ-existant world?
• What do researchers dislike about Verkle?
• Can we actually harden Verkle?

The overall goal of this post will be to answer these questions and try to share all the knowledge obtained within the process.

What problem are we actually addressing?

The motivation for Verkle trees is clear. Ethereum’s state is growing.

And that increases the demand on hardware for anyone that wants to participate within ethereum’s protocol.

Imagine being a node that doesn’t hold the whole ethereum state. That would dramatically reduce the requirements and therefore lower the entry barrier to more participants within ethereum network.

One could say, well, I’ll just ask full-nodes for the witness related to each block. Such that I don’t need to store it locally and instead I’ll fetch it every time I need it.
This presents some problems:

• You need a proof that attests the witness received are indeed the right ones.
• Taken from the Motivation section of EIP-6800 itself

A witness accessing an account in today’s hexary Patricia tree is, in the average case, close to 3 kB, and in the worst case it may be three times larger. Assuming a worst case of 6000 accesses per block (15m gas / 2500 gas per access), this corresponds to a witness size of ~18 MB, which is too large to safely broadcast through a p2p network within a 12-second slot.

As seen, witness correctness proofs require a huge cost in terms of space and disk access. Which will only increase overtime.

• Proofs are depth-dependant. Ie. The more the tree grows in the future, the larger the depth. The bigger the proofs.
• The endgoal would be that blocks are self-contained. ie. anyone that receives a block, can attest its validity without the need of holding the whole ethereum storage locally. But with current MPT witness-size & proof-size. This is not even imaginable as shown in the second point.

This is what statelessness promises to fix and what Verkle trees were a solution for.

What properties did we actually like from Verkle?

Let’s briefly explain several of the reasons why we liked Verkle:

Storage-proof size

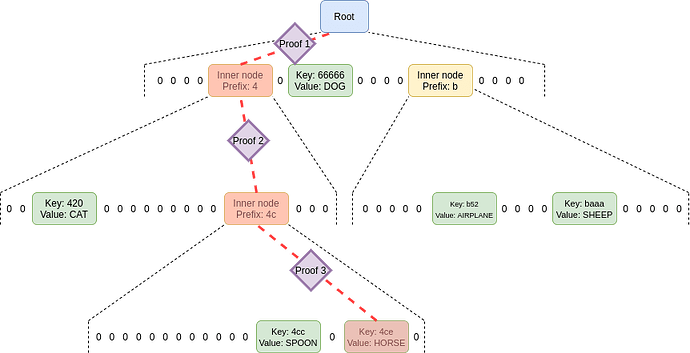
This is how a a Verkle Tree and proof of storage of a value looks like (taken from Vitalik’s post):

1. No sibling nodes are needed for storage verification. Which allows for a massive increase in arity and decrease in depth of the tree.
2. Verkle tree proofs require a VC (Vector Commitment) opening proof per tree-level (depth-wise). This means the bigger the arity, the lesser openings we have per proof (as depth decreases wrt arity).
3. The more leaves/state you need to prove, the more Verkle shines.
   If you pay close attention, for the previous picture, we can see that proving the inclusion of HORSE requires 3 VC openings + some extra things.
   With MultiProofs the overall size of a proof for ANY AMMOUNT OF LEAVES being proven Sums up to 4*32+576=704 bytes + 32 bytes * commitments_in_paths.
   This means Verkle proofs of storage are smaller compared to MPT and Binary trees FOR ANY AMOUNT OF LEAVES PROVEN.
4. Verkle Trees enable the capacity of profiting from differential-updatability(which can be less formally understood as homomorphically additive properties). This means we need a lot less data to be fetched from the tree. So you can have a very large arity and not pay the storage costs for it!

This is why I say that Differential Updatability is critical for PQ-Verkle trees to make sense

Useful short notes on Differential Updatability vs. Stateless Updatability

- A statelessly-updatable vector commitment (VC) is one that can be updated to reflect changes in an entry using only local information about that change, without needing the entire original vector or additional secret state. In other words, given an old value and its new value at some index, one can compute a token to update the commitment and the corresponding proof for that index, more efficiently than recomputing from scratch. - A differentially-updatable VC is an even stronger notion: the update can be computed using only the difference between the new and old entry ($\delta$), rather than requiring both values separately. In such schemes the commitment is typically homomorphic or linear in the entries, so applying the difference $\delta$ (e.g. adding $\text{m'}_j - m_j$ in an exponent or polynomial) correctly updates the digest and proofs. Every differentially-updatable scheme is inherently statelessly-updatable (since knowing δ is even less information than knowing the old and new values)

IO performance and improvements

Verkle trees are the best tree-like structures regarding IO performance.

• There are less nodes overall in the tree thanks to the sparsity of itself.
  This, essentially means that Verkle trees yield smaller trees (storage-wise).
• Accesses to neighbouring positions (e.g. storage with almost the same address or neighbouring code chunks) becomes much cheaper to access. Thus, resulting in IO read rate improvements facilitating possible decreases for opcodes like SLOAD or L1SLOAD.
• Each internal node only needs to store the commitment to itself, and no reference to its children. This leads to smaller trees, less IO interactions/fetching, smaller opening witness and overall, better performance.

As said by @gballet: Binary trees might be massaged enough that you can recover some of the same savings, but the lack of possibility to be differentially-updatable will make it difficult to achieve the same results.

• With Differential-Updatability, the amount of nodes fetched in order to verify a storage-proof is significantly lower. Thus, improving overall performance of IO proving ops.

From @gballet: […] the IO gain comes from the verification part (no need to read the disk). And also that each node is smaller since it contains no difference, so the iterator sweep of the db is much faster.

Why does it matter all this matter? Because IO is the biggest performance killer within ethereum-block execution, and so the less data you write at the lowest rate is always better.
Also, the smaller tree requires a smaller DB, and DB random reads are a pain in terms of performance, and the larger the DB is, the more painful random reads become.

Would Verkle be the best solution if Quantum Computing is not considered?

Short answer, Yes (with KZG undoubtebly, but that’s another discussion).

Storage Proofs

An important remark here is that while Verkle Trees provide the “data layout” for extremely efficient proofs to happen. The reality is that IPA’s(Inner Product Argument) VC and IPA-MultiProof scheme are actually the ones doing the heavylifting.

One can identify quickly that the proof size that MultiProofs yields its based on 2 things.

• IPA (the core primitive of bulletproofs) yields succint and very short proofs thanks to Elliptic Curves being its core engine (among other things that I won’t dive into here).
• Commitments are extremely short. (1 Bandersnatch EC point \approx 32 \text{bytes}) So even though commitments need to be sent alongside the proof, they are actually the same size as a hash. But actually aggregate A TON of leaves or intermediate nodes.

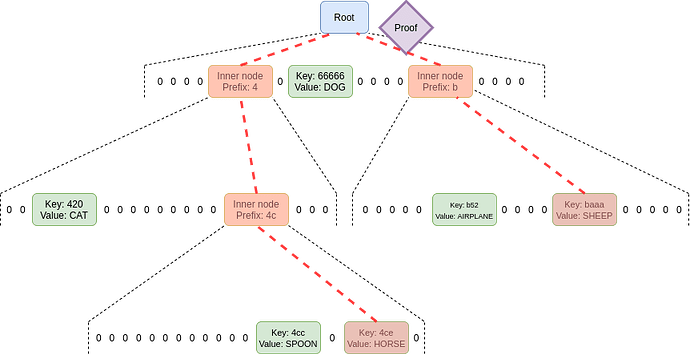
Notice in this image how we actually reduced the 3 VC opening proofs to a single IPA proof that proves all of them.
This, when proving state transitions in Ethereum translates into reducing ~(3000-6000) opening proofs to a single IPA proof.

IO space/performance

In terms of space the tree takes in disk and performance on reads and random access, Verkle trees would definitely be the best solution.

What do researchers dislike about Verkle?

Well, this is feedback I’ve been trying to gather. Specially considering the alternatives proposed so far: (Binary Trees and ZKEVM-MPT).

PQ-resistance:

This is definitely a reason. And multiple concerns/arguments come into play here:

1. State-tree conversion is a delicate and complex procedure which could take weeks or even months to be performed by all nodes. It’s a risky thing to do. And going non-PQ Verkle, we would be forced to do 2 tree migrations at least (MPT → Verkle, Verkle → some_PQ_alt).
2. ZKEVMs/ZKVMs are PQ-secure (most of them at least, like plonky3-based ones). BUT in order to aggregate all FRI/WHIR/WHATEVER sub-proofs into a single one, they need to have a distributive way to split the Fiat-Shamir not making it dependent of each RISCV execution trace chunk.
   This is a decent blocker in proving performance for them. And one way they’re looking to solve this is using Elliptic Curves again!. Which will turn ZKVM performance dependant on PQ-insecurity (though alternative solutions exist, just haven’t been deeply checked).

This is a much larger thing to explain, the TLDR is that these ZKVMs need to use elliptic-curves to decouple FS and make it independant from RISCV execution-trace chunks/overall trace. This, allows them to parallelize a lot more making memory-checking (but potentially lookups and permutation arguments much faster to process**). See more in this twitter thread.

What this comes to say, is that we assumed most of ZKEVM/ZKVM solutions were PQ-secure. But if they actually need Elliptic-curve-based arguments to scale up and give us the golden real time proving, we loose the PQ property making ZKVM/ZKEVM approach even more dubious than it already is (for speed and security considerations).

3. So Binary Trees seem to be the best solution atm(unless PQ-Verkle is a thing and is good).
   The issue with them is that we know proof-size is not going to be nice.
   Preliminary numbers give ~32 levels of depth of the tree (considering unifying all storage, so code and everything being in the tree too).
   That means for a single leaf, we need to provide \pi = 32\text{nodes} * 32\text{bytes} \approx 1\text{kB}.
   Considering we change ~(3000-6000) leaves on each state change, although not linearly, this doesn’t scale well.
   One could try to use WHIR or some other PIOP to construct a proof that verifies all these openings effectively “compressing” them (recursively aggregating in reality).

   The main issues that this falls into (after not so rigorous nor deep discussions with @WizardOfMenlo) are:

   • Since we loose all hopes of Opening-proof aggregation (no additively-homomorphic properties exist), we need to prove all the Opening proofs correctness by going THROUGH EACH ONE OF THEM.
     Doing some quick numbers:

     If we take 6000 node updates, at 256 (current arity) items per level, we get to:

     sage: numerical_approx(log(6000*256,2))
     20.5507467853832
     

     That means 2^{20} opening verifications. I can’t estimate how does this translate to constraints. But certainly would expect something over 2^{23}.
   • It is difficult to actually imagine any hash-based scheme yielding sub-MB proofs except from WHIR itself. And does it with some tradeoffs:
     
     

   Also, this would mean that we loose the Differential Updatability property. Which significantly impacts IO-related performance in disk reads/access.

That being said, remains to be seen and further explored how good this solution could actually be. As 100kB-1MB proofs aren’t crazy at all (for what PQ-proofs refers to). This comes to say that this isn’t a bad idea at all. Rather not a really good one apparently.
A short, non-technical explanation for this is that as Sanso mentioned to me some time ago: Elliptic Curves are an anomaly. They have it all (Short proof sizes, fast provers, additively-homomorphic properties, pairings…).
We got used to it and now it seems to us that the alternatives (specially PQ-schemes) aren’t close. But we need to accept that these weren’t the rule, rather the exception.

ZK-(un)friendliness

Arithmetizing problems in SNARKs is (and might always be) a huge deal-breaker in terms of performance.

One of the most challenging aspects of working within SNARK circuits is the optimal arithmetization of what’s known as “wrong-field arithmetic” or simply “foreign field arithmetic.” This operation performs so poorly that people have historically addressed the issue by embedding elliptic curves. I did it myself here for Curve25519. When working within SNARK circuits, we represent our witness using a finite field.

Note: You are not guaranteed to find a curve that possesses the properties you need, nor is it guaranteed to exist. Additionally, such a curve might lack pairings—due, for example, to the Hasse bound—or simply because it cannot be constructed with certain parameters.

In STARKs, however, this is not even an option; we always need to emulate arithmetic over foreign fields. This is what all ZKEVMs do nowadays, with Secp256k1 as an example.

Verkle, in this case, uses Banderwagon/Bandersnatch. You can see more details in this post from Kev: Understanding The Wagon - From Bandersnatch to Banderwagon. To simplify, any proving system (in fact, all ZKEVMs) must simulate arithmetic modulo Banderwagon’s base field. As mentioned earlier, field emulation is slow, difficult to reason about, and a pain to implement.

This is clearly problematic. We all know that, but it can be done—and at least benchmarked (to my knowledge, no results have been published).

Can we actually harden Verkle?

If you made it here, congrats! You’re arriving at the most exciting part!

ZK-(un)friendliness

PQ-Verkle based most-likely on lattices might not be anything close to how bad the arithmetization of elliptic curves is.

Not because they are simpler. But because usually within the polynomial rings used there, we end up working with primitives of ~64bytes.
In particular, we could try to use a field like Goldilocks over polynomial ring. That could basically make this “native” for ZKEVMS or STARKS.

This remains to be seen. And it’s a big unknown. But I’d definitely expect the situation to be better than in the case of Verkle+Bandersnatch one.

PQ-resistance

This is definitely the biggest concern against Verkle trees. In order to solve this we need the following:

• A VC that yields small opening proofs.
• A VC that yields aggregatable/foldable/accumulative opening proofs resulting in significant size-reduction for state proofs.
• The resulting aformentioned aggregation results are actually small too.
• The VC or the method to aggregate the openings require no setup.
• Everything is efficiently-computable by the block-proposer hardware requirements within a reasonable performance that allows for enough time for block propagation.
• Commitments are small (EC-point size or less, so \approx 32\text{bytes}).

Details to pay attention to

Most of the literature on PCS targets:

1. Commit to VERY LARGE POLYNOMIALS.
2. Produce succint opening proofs.

It’s important to notice here that we actually don’t care about the first one. And most likely the second one isn’t crucial.

See, tree-level’s width (arity) within Verkle is 256 elements. And could potentially be 1024 or more as advised by some back then. A VC scheme is designed to commit to vectors of lots of elements. Sets of \approx 2^{30} elements. This means there are potential tradeoffs we can take there to actually trade committed vector-size by proof-size or verification complexity among others.

On another note, a lot of PCS and VCS have the goal of providing succint opening proofs.
BUT, again here, succint opening proofs might not be needed. Specially considering we want to then aggregate them. It’s the result of the aggregation what needs to be succint (or close to it).
We can go even further. Even a linear verifier or quasi-linear would be good.
This is because the vectors we commit to are really small. So computations that are \approx \text{O}(k*N + c) where \text{\{k, c\}} aren’t some crazy constants would be run within ms or less.

SoTA in PQ-Vector commitments (specially lattice-based ones)

Currently, there are some recent works which have achieved outstanding results in terms of opening-proof size.

“Vector and Functional commitments from lattices” (https://eprint.iacr.org/2021/1254.pdf)

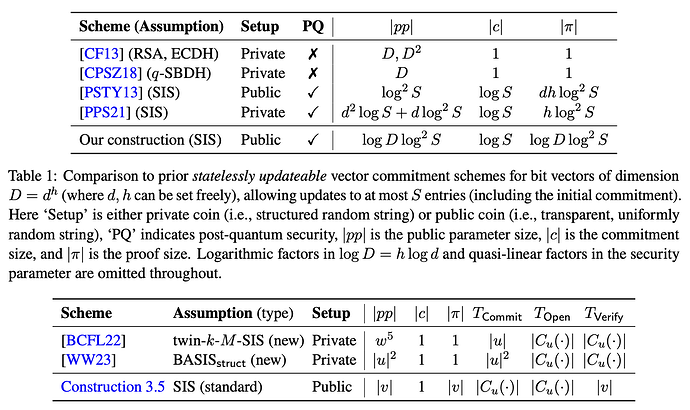
Generally, pre-2020 lattice VCs either had large proofs or relied on a trapdoor setup, limiting their practicality. An example is this work (PPS21), which yields post-quantum VC with shorter proofs (compared to prev literature like Libert et al. work on SIS-based commitments and ZKPs in 2016) but at the cost of a private-key setup (a trapdoor generated by an authority).

So as a summary, with this scheme, we sadly get:

• Trusted setup requirements.
• Not so good assymptotics. Much worse than Merkle trees.

---

Scheme introduced in “Polynomial Commitments from Lattices: Post-Quantum Security, Fast Verification and Transparent Setup” (https://eprint.iacr.org/2024/281.pdf)

This work bridges some initial discoveries made in Module-SIS problem-based schemes to the first really practical scheme.

In particular it has commitment and proof size too big for our purposes.

So not many tradeoffs that we can apparently take here without overcomplicating or significantly increasing proving time.

---

“Functional Commitments for All Functions with Transparent Setup and from SIS” (https://eprint.iacr.org/2022/1368.pdf)

A really nice suggestion made by Dr Ngoc Khanh Nguyen (one of the main experts within the field) was this work.

The scheme introduced here, aside from being statessly updatable, improves over prior SoTA stablished in PPS21.
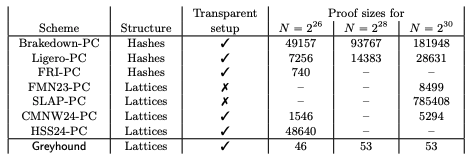
One can see why by looking at the table:

We get rid of the squared terms in complexity for the parameters size. As well as the linear size in the proof.

Overall, this scheme looks super promising for our use case and one of the ones I’d be interested on analyzing much more.

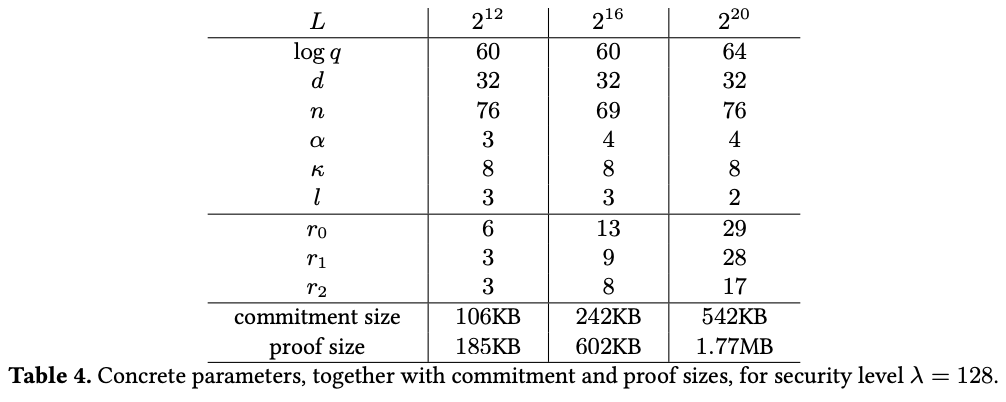
• O(\text{log}^2)-sized proofs for sets/vectors of at most 1024 elements yields insanely small opening proofs.
• Statessly-updatability is an awesome feature for Verkle.
• Commitment/Proving time aren’t exponential nor anything similar. So we don’t need to worry.

Only one question remains for this scheme, which is if we can acually integrate a MultiProofs-like solution which accumulates all the opening proofs resulting on a single final one.

---

Greyhound (https://eprint.iacr.org/2024/1293.pdf)

Note that sizes here are in kB

So this is one of the latest achievements in PCS-land. Mainly, it obliterates all previous work while also achieving much faster verifiers in some cases.

Greyhound itself, can be turned into a VCS by interpolating the values polynomial with another polynomial representing the position indexes where values are stored.

Khan suggested that while you can obtain a VCS from it, it’s not obvious if it can actually be statessly-updatable. And which would be the tradeoffs that one needs to to in order to get such benefits.

What is certainly possible, is to take all the openings needed in a state proof, batch them and use Greyhound to get a O(\sqrt{N})-sized proof which can then be thrown to LaBRADOR if needed.

If you’re interested on understanding the SoTA of the field, the section 1.1 of this paper does a quite good job at doing so. At least with all the related work to this paper.

Aggregatability

LaBRADOR usage is available but not desirable.

Although we could (as suggested by both Khan and @WizardOfMenlo) use a lattice-based proving scheme like LaBRADOR in order to help getting a sub-linear sized proof. This would significantly increase the complexity of the overall solution (the only implementation in existence atm is quite optimized but also extremely complex to use.).

So unless someone with a lot of courage to take GitHub - lazer-crypto/lazer and rewrite it exists, I’d much rather prefer trying to exploit additively-homomorphic properties to try to accumulate opening proofs without involving proving schemes.

Using hash-based proof systems for accumulation

One potential path forward is to use a proving scheme like WHIR which can yield decently-sized proofs which can be succintly verified (\lt 100\text{kB}).

WHIR would drop the requirement for the Opening Proofs to be aggregatable. Thus, enabling more schemes to be used.

One of the good things about that is that hash-based proving systems are widely deployed and hashes have been studied for long time. So a lot less “exotic” solutions are much more likely to be secure and therefore, have higher chances making it to mainnet.

Doing some quick numbers:

If we take 6000 node updates, at 256 (current arity) items per level, we get to:

sage: numerical_approx(log(6000*256,2))
20.5507467853832

2^{20} nodes to update in worst-case situations (more in the future ofc as we plan to raise gas_limits once statelessness hits mainnet).
What could we expect from WHIR here? As in proving-time and proof-size? This questions should be answered for the VCs that we potentially could use.
Such that we can discard or heavily consider some of them.

Opening-accumulation via additive-homomorphism

As in Multiproofs solution, one would like to compress opening proofs produced at each tree-level by the vector commitment (VC) scheme, while keeping constant-size (or quasi-constant) for the resulting artifact while doing so.

This essentially means that we have extremely short proofs, a similar result to what we see in the Beacon chain when Bls signatures get aggregated into a final one that has the same size as any of the original ones.

It remains to be seen (at least I’m not aware) if there are any VC schemes that have such properties and are PQ-secure.
But there are definitely proving schemes that can help us to get there as IPA is doing in MultiProofs.

Of course, the preference would be to not need those, as this adds another component within the overall solution and makes it more complex. Which is never desired.

Differential Updatability

From the schemes shared previously, only a few were compliant with this feature.

Remains to be seen if for awesome schemes like Greyhound, achieving this incurrs into a big cost or tradeoff.

Nevertheless, it’s important to remember that THIS IS A MUST HAVE FEATURE. As without it, all our aggregation and node-updatability plan to efficiently remove tree-size gets truncated.

Conclusions

PQ-Verkle would tick all the boxes as the main contender for statelessness and storage structure to be used witin ethereum.

I think it’s at least worth investing a bit of time on analyzing a bit more deeply how much we can actually get from this. And which would be the realistic alternatives.

And it’s equally important to keep ALWAYS in mind, that a good solution isn’t something that works well now. Rather something that will work well when we 10x block gas limits!

I’ve met various people while working on this idea that are working on similar things. And researchers seem to find it an attractive problem to tackle. Which motivates the believe that we might be into something. We weren’t the only ones looking into it and we’re already syncing with these researchers to understand their approaches and ideas/results.

As for the most promising path atm?
Well, it seems that https://eprint.iacr.org/2022/1368.pdf is one of the best ways to go atm.
Specially since a linear-verifier isn’t an issue when we have openings of 1024 elements at max.
Not only that, but is also important to remark that is one of the few SIS-based scheme that supports differential-updatability.

So one of the next steps that we should likely take is to actually evaluate what’s the best approach for opening proof aggregation. Followed up by an identification of the weakest points of the solution (if any) and a comparison against other proposals.

Finally, it’s also important to acknowledge that this is yet another complex solution for ethereum.
I think the overall protocol complexity discussion should take place elsewhere. But definitely is a conversation that will need to happen. And not for this proposal only.