A sketch for a STARK-based VM

[bobbinth]

This posts provides a (very rough) sketch for a virtual machine such that execution of arbitrary programs on this machine can be verified with a single STARK. To make the VM practical, the instruction set is not Turing-complete but I think it may still be powerful enough to cover a large set of smart contract use cases.

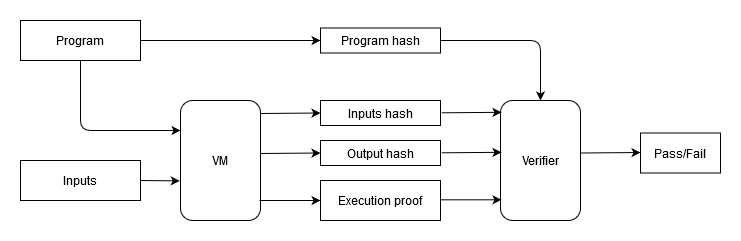
The diagram below illustrates the basic concept:

In the above:

1. The VM does the following:
   a. Takes 2 inputs: a program and a set of inputs for the program,
   b. Executes the program with the given set of inputs,
   c. Outputs hash of the inputs, hash of the outputs generated by the program, and a STARK proof attesting to the correct execution of the program.
2. The verifier does the following:
   a. Takes the hash of the program, hash of the inputs, and hash of the outputs, and uses them to verify the STARK proof.

Potential advantages of this approach:

1. The program, the inputs, and the outputs are fully private (they are never revealed to the verifier).
2. A single verifier can verify any program executed on the VM (e.g. a verifier can be a single on-chain contract).
3. Since the structure of the STARK is the same for all programs, batching of proofs using another STARK (or a SNARK) should be much easier to accomplish.

In terms of execution speed, my very rough gestimate is that an optimized prover on a CPU with several cores should be able to get to about 1 KHz (1,000 instructions / second), and with specialized hardware it may be possible to get to some MHz.

Just to say it again: this is a very rough sketch and the description below is by no means complete. It should be enough to illustrate the basic ideas though, and I’m curious if anyone sees any major issues with these.

vm overview

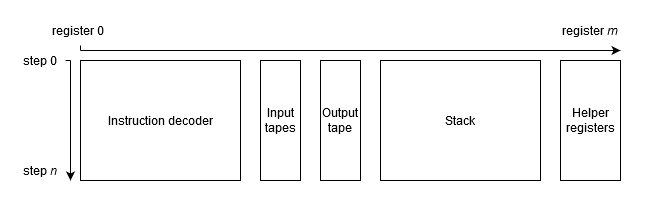
At the highest level, the VM is a stack machine. The execution trace consists of several sets of registers each having a separate function as shown below:

1. Instruction decoder is perhaps the “heaviest” part of the trace. It is responsible for decoding instructions into their binary representation and building a continuous hash of the executed instructions. It would require roughly 14 registers.
2. Input tapes - there would be two input tapes. One of the tapes will contain inputs to be pushed onto the stack, and the other tape with “hints” to aid in execution of certain instructions. Similar to program instructions, the input tape is contentiously hashed so that by the end of the execution the tape is reduced to a single hash value.
3. Output tape - this would be the tape that defines output values of the program. Though, there might be better ways to handle outputs.
4. Stack registers will represent the stack with the first register being the top of the stack, the second register being the second from the top etc. It is important to note that the number of stack registers does not need to be fixed. Without loss of generality, it can be set to any reasonable number as required by a specific program (e.g. 4, 20, 80). This is because traces of all “unused” stack registers are just zeros, and this can be succinctly communicated to the verifier.
5. Helper registers would be a small set of registers (e.g. 3 - 5) which could aid in execution of certain complex instructions (e.g. hashing, elliptic curve operations).

Overall, my guess would be that a typical program might require 30 - 40 registers, though, I might be very off on this.

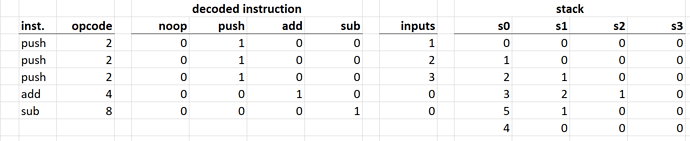
Here is an example of how an execution trace of a program could look like. It omits and simplifies a lot of details, but should illustrate the concept:

Here is what’s happening here:

1. First, values 1, 2, and 3 are pushed onto the stack.
2. Then, top two values are popped from the stack, added, and the result is pushed back onto the stack.
3. Lastly, top two values are popped from the stack, the second value is subtracted from the first, and the result is pushed back onto the stack.

A transition function for the above could be simply described as follows:

s_{n+1} = f_{noop}(s_n) \cdot d_0 + f_{push}(s_n) \cdot d_1 + f_{add}(s_n) \cdot d_2 + f_{sub}(s_n) \cdot d_3

where:

• s_n and s_{n+1} are the current and the next states of the stack.
• d_i are the bits of decoded instruction.

This is a somewhat inefficient way to describe the transition function. In reality, there wouldn’t be a single register per instruction, but rather a combination of several registers would be used to encode all instructions. However, there still would be a single transition function per instruction, and a combination of all instruction-specific transition functions would describe the VM transition function. The number of instructions could be kept relatively small (e.g. 40) and the degree of the VM transition function does no need to exceed 8.

programs

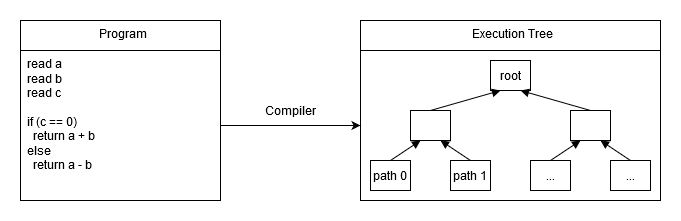
One of the challenges of defining a VM such that a single STARK can be used to prove execution of an arbitrary program is handling of conditional branches. One simple way to handle these is to decompose the program into all possible linear execution paths and put these paths into a Merkle tree (this approach is somewhat similar to Merkelized Abstract Syntax trees). Here is an example:

In the above:

• path 0 might be push push push assertZero add
• path 1 might be push push push assertNotZero sub

The biggest limitation of this approach is that programs with deep conditional logic become impractical, and some programs (e.g. with unbounded loops) become impossible. Realistically speaking, programs with over a million possible execution paths are probably too complex and this can be reached with about 20 nested (or consecutive) if/else statements. There might be some ways to mitigate this limitation - though, I haven’t come up with any yet.

One possible (though probably rather weak) advantage of this approach, is that the explicit need to list all possible execution paths can help with formal verification of the program.

instruction set

The instructions could be encoded as 8-bit values (other approaches are possible, though, 8-bit representation has a number of advantages). These 8 bits could be split into 2 sets:

1. 3 bits to encode 7 “high-degree” instructions - i.e. instructions of degree 4 or 5
2. 5 bits to encode 31 “low-degree” instructions - i.e. instructions of degree 3 or lower

This in total gives a set of 38 possible instructions (though again, this could be changed if needed). Here is a list of some of the possible instructions:

Instruction	Description	Degree	Alignment	Steps
noop	do nothing	1	1	1
verify	fail if top of the stack is not 0	1	1	1
push	push input onto the stack	1	1	1
pop	remove value from the top of the stack	1	1	1
swap	swap top 2 values of the stack	1	1	1
dup	duplicate top stack value	1	1	1
add	pop top 2 values, add them, push the result onto the stack	1	1	1
sub	pop top 2 values, subtract second from first, push the result onto the stack	1	1	1
mul	pop top 2 values, multiply them, push the result onto the stack	1	1	1
div	pop top 2 values, divide first by second, push the result onto the stack	?	1	1
eq	pop top 2 values, compare them, and push 1 if they are equal, 0 otherwise	?	1	1
neq	pop top 2 values, compare them, and push 0 if they are equal, 1 otherwise	?	1	1
lt	pop top 2 values, compare them, and push 1 if first is less than second, 0 otherwise	?	256	256
gt	pop top 2 values, compare them, and push 0 if first is less than second, 1 otherwise	?	256	256
phash_1	pop top stack value, hash it using Poseidon hash function, push the result onto the stack	5	64	64
phash_2	pop top 2 values, hash them using Poseidon hash function, push the result onto the stack	5	64	64
rhash_1	pop top stack value, hash it using Rescue hash function, push the result onto the stack	3	32	32
rhash_2	pop top 2 values, hash them using Rescue hash function, push the result onto the stack	3	32	32
ec_add	pop top 4 values, interpret them as x, y coordinates of 2 elliptic curve points, add the points, and push the resulting x, y coordinates onto the stack	4	2	1
ec_dub	pop top 2 values, interpret them as x, y coordinates of an elliptic curve point, double the point, and push the result onto the stack	4	2	1
ec_mul	pop top 3 values, interpret the first value as a scalar and the other 2 values as x, y coordinates of an elliptic curve point, perform point multiplication, and push the result onto the stack	5	256	256
ver_sig	pop top 5 values, interpret them as components of Schnorr signature, push 1 onto the stack if the signature is valid, 0 otherwise	5	256	256

As can be seen from the above, some instructions may take more than a single step to execute, and may need to be aligned on certain multiples of steps. When an instruction doesn’t align, noop instructions can be used to pad the instruction sequence.

Again, these are just for illustrative purposes. Some of these might not make sense to have, others might be missing (e.g. an instruction to help with Merklet branch verification).

memory

Memory can be added by having a dedicated register which holds a root of a sparse Merkle tree committing to the memory state. Memory read/write instructions can be added. The read instruction would provide a Merkle path to the desired memory slot, and the write instruction would update the state of the Merkle tree as needed. This approach would be rather inefficient, and other approach might be possible.

outstanding questions

The biggest outstanding questions in my mind are:

1. Is this VM sufficiently powerful to be useful in describing smart contracts?
2. Is there a better way to handle conditional branches?
3. Is there a better way to handle memory access?

I also might be missing something. So, any thoughts or feedback are appreciated.

[denett]

A very cool idea!

@bobbinth

Is there a better way to handle conditional branches?

You have described several instructions that do comparisons and push either a 1 or a 0 to the stack. You can use these to eliminate the conditional branches.
Your example could be written as:
d=(c==0)?1:0;
return d*(a+b)+(1-d)*(a-b);

I guess you can write most conditionals this way. It is less efficient, but you can do as many conditionals as you like.

Loops with a fixed number of iterations have the same execution trace as long as the conditionals are removed. Open ended loops are still problematic, because we do not now how many times we have to do the loop. I don’t know if you can do it in a STARK, but it might be possible to tackle this problem by using two hash stream for the instructions. All instructions are added to the first stream. When a new instruction “Wrap” is executed the hash of the the first stream is send to the second stream and the first stream is cleared. When the new instruction “WrapLoop” is executed, we do the same, but only add the hash to the second stream if it is different from what was last added to that stream. A program always ends with a “Wrap” instruction, so the output of the second hash stream is the result of all executed instructions.

We start an open ended loop with a “Wrap” and end the loop with a “WrapLoop”. We can repeat the instructions between theses instructions as many times as we like (at least once) and still get the same instructions hash result.

[bobbinth]

Thank you!

I am not sure I fully understood the idea for handling of conditional branches. It makes sense that we can push d=(c==0)?1:0 onto the stack, but then we need to execute 2 instructions (a+b and a-b) in parallel. This would require a separate set of registers for each parallel instruction and would quickly become impractical - unless I’m missing something.

This approach can probably be used to handle conditional expressions (i.e. if without else), and then this can be expanded branching. With such an approach, the example from original post can be rewritten like so:

read a
read b
read c

if (c == 0)
  r = a + b
if (c != 0)
  r = a - b

And the execution path for this would be something like:

push a
push b
push d = (c == 0) ? 1 : 0
iffadd  // pushes d * (a + b) onto the stack
push a
push b
push d = ( c=! 0) ? 1 : 0
iffadd // pushes d * (a + b) onto the stack
add    // adds the results of 2 branches 

Is this what you had in mind?

---

Edit: thinking about this some more, it seems like this approach would generalize pretty nicely to any conditional logic (and should remain practical for moderately complex logic). And combining this with using a Merkle tree for different execution paths, would greatly expand the set of potential programs that can be executed on such a VM. Very cool!

[burdges]

I know SNARKs always represent themselves with actual circuits. Why a stack machine here?

Are you simply making sacrifices merely to make this act like a normal computer? Or does the STARK actually gain anything from this stack model?

[bobbinth]

STARKs have some advantages over SNARKs for describing virtual machines because STARKs circuits (called AIR) can describe unbounded computations. So, you can build a STARK circuit which describes a single cycle of a virtual machine, and then use it to generate proofs for any number of VM cycles.

My understanding is that to achieve something similar with SNARKs, you’d need to use infinite recursion.

As to why stack machine, it was pretty easy to design AIR for a stack machine rather than a register-based machine. The core idea here though is that there is a single AIR (a single circuit) which can be used to generate proofs for general computations. So, you don’t need to come up with a different circuit for each program.

[burdges]

STARKs have some advantages over SNARKs for describing virtual machines

I knew this …

because STARKs circuits (called AIR) can describe unbounded computations.

but not this, thanks! I should read more about STARKs really.

So, you don’t need to come up with a different circuit for each program.

Any idea how much this costs over doing a hand optimized AIR circuit that exploits non-determinism agressively though?

We’ll want DSLs for coding zk proofs of course, but I’d expect a top priority to be retaining roughly the full performance of AIR, R1CS, etc. Importantly, if the DSL captures AIR more fully then you’ll express far more inside the DSL’s standard library, so users actually learn much more when they read the standard library code. We’re quite a ways from doing optimal DSLs for AIR, R1CS, etc. I guess.

[bobbinth]

@burdges

Any idea how much this costs over doing a hand optimized AIR circuit

short answer
It really depends on the computation: for very simple computations, hand-optimized AIRs could be 10x more efficient. But for more complicated computations, general-purpose VMs should be on par with hand-optimized implementations.

longer answer
Designing efficient AIR for general computations is a pretty complicated task. It is kind of like writing programs in machine code rather than in a high-level language. For simple things, a human may be able to write very efficient hand-crafted machine code, but for more complicated systems, a compiler will usually do a much better job.

Same with AIR: for something as simple as computing a hash-chain using Rescue or Poseidon hash function, we can hand-craft very efficient AIR. Based on my very high-level benchmarks, such hand-crafted AIR would outperform computing a similar hash chain on Distaff VM by a factor 5x - 10x.

But as you try to write AIR for more complex computations this difference starts to shrink. In this blogpost, StarkWare estimates that for the types of computations they are dealing with, their STARK-based VM (called Cairo), under-performs hand-crafted AIR by just 30%. And they even suggest that for some computations the VM may be more efficient than the hand-optimized approach.

It is possible that at some point someone will build a compiler that can translate complex computations into very efficient AIR - but this would be a huge undertaking (perhaps significantly more complex than building traditional compilers). Plus, there are several other advantages to the VM-based approach (where you have single AIR for all computations) which I think trump compiling computations into distinct AIRs.

[vbuterin]

@bobbinth

STARKs have some advantages over SNARKs for describing virtual machines because STARKs circuits (called AIR)

I think the AIR designs that are available to STARKs and PLONK-style SNARKs are identical, no? Or am I missing something really important there?

[bobbinth]

To be honest, I’m not super familiar with capabilities of PLONK - so, I might be the one missing something here. But here is how I thought about it:

With STARKs, you can define AIR for a single cycle of the VM, and then the same AIR can be used to generate proofs for 1 million, or 1 billion, or 1 trillion VM cycles (the number of cycles can be unbounded for all practical purposes). So, the verifier needs to know just one AIR to be able to verify any computation.

My understanding about how SNARKs work was that for each computation you need to define a different circuit. So, a circuit for 1M cycles would be different from a circuit for 1B cycles etc. In this context, the verifier would need to know verification keys for each number of cycles to verify computations. If that’s not the case for PLONK-style circuits, then my original statement was wrong.

[MariusVanDerWijden]

As I understood your sketch, your propsing a stack machine inside a stark. Why are you specifying the helper registers? Aren’t they an implementation detail or will they be part of the proof too? If so there should be operations to read and write these registers in order to speedup execution imo.

I think mixing both paradigms (stack based and register based) together will increase the complexity of the overall approach unnecessarily.

[bobbinth]

There is a bit of terminology mixing here. “Register” in a context of a STARK proof refers to a column of an execution trace. So, it is not the same as “register” in a register-based machine.

Distaff VM is a pure stack machine - i.e. as far as the user is concerned, there are no registers - you do everything on the stack. You can check out the current instruction set here.