Motivation
An optimistic rollup periodically submits L2 transactions in batches to L1 with each batch being
(T_n, h(S_n))
where n is the batch index, T_n is the list of L2 transactions, S_n is the post-state in a set of KV pairs evaluated by the rollup proposer, and h() is a hash function of the state, e.g., returning the root hash of a Merkle Patrica Tree (MPT) representing the state implemented by EVM.
If the proposer submits an incorrect off-chain execution result of batch n, i.e., h(f(S_{n-1}, T_n)) \neq h(S_n) where f() is the state transition function, a challenger can challenge the result on-chain via an post-state fraud proof. To determine the proposer or the challenger is faulty, the fraud proof will run an interactive on-chain dispute game with inputs h(S_{n-1}), T_n, and h(S_n).
This optimistic rollup approach requires each batch to contain the post-state hash. However, one performance bottleneck of L2 execution is to compute the post-state hash in MPT h(S_n) by the L2 proposer for each batch (e.g., by the sequencer), which results in a large number of IOs for reading/writing the MPT.
An approach to accelerate the execution is to replace the MPT with flat KV, adopted by Erigon / Reth stage sync and fast EVM execution idea here. In our internal benchmark with Ethereum mainnet data, the performance gain of flat KV can be 2x or more. Furthermore, the gain increases as the state size increases. However, how to apply flat KV in L2 execution while enabling fraud proof is an open question.
L2 EVM Execution with Flat KV
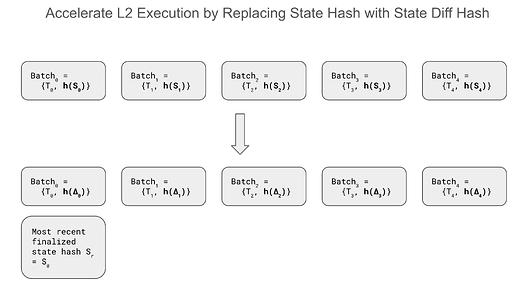
The proposed idea will submit an L2 batch as
(T_n, h(\Delta_n))
where \Delta_n = S_n - S_{n-1} is the set of the states (KV pairs) in difference. Since we do not need to post h(S_n) for every batch, the L2 transactions can be executed on a state implemented by a flat KV storage. Further, since |\Delta_n| << |S_n|, the hash of the state diff can be computed very efficiently.
The L1 rollup contract also maintains the most-recent finalized state hash as
h(S_r)
where r is the batch index of the most-recent finalized state hash. Note that h(S_r) can be also updated by a sequencer, however, it does not have to be updated as frequently as the batches. This means that it is possible that n >> r.
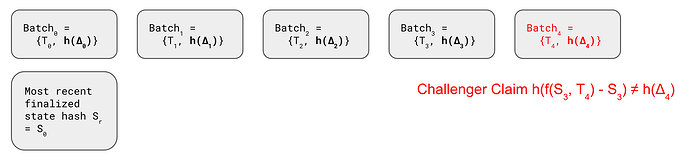
When a challenger finds h(f(S_{n-1}, T_n) - S_{n-1}) \neq h(\Delta_n), it could initiate a two-stage fraud proof and verify the claim as follows.
Two-Stage Fraud Proof
Initial Challenge with Claim h(S'_{n-1})
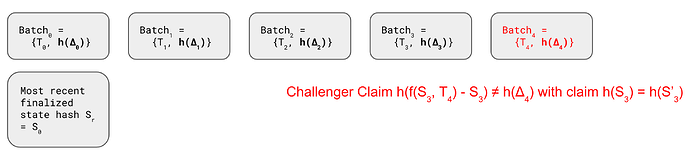
To initiate a challenge, the challenger will file a on-chain claim h(f(S_{n-1}, T_n) - S_{n-1}) \neq h(\Delta_n) with an additional claim of the post-state hash h(S'_{n-1}) of batch n-1.
Depending on the response of the sequencer, we have two cases
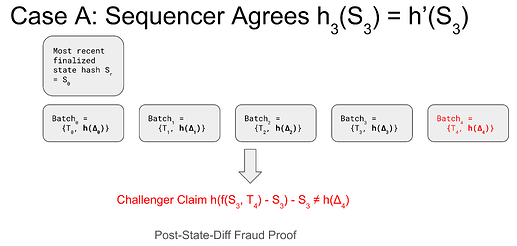
Case A: Sequencer Agrees h(S'_{n-1})
If the sequencer agrees that the post-state hash of batch n-1 is h(S'_{n-1}), then the challenger claim reduces to
h(f(S'_{n-1}, T_n) - S'_{n-1}) \neq h(\Delta_n)
with on-chain inputs T_n, h(S'_{n-1}), and h(\Delta_n).
Similar to post-state fraud proof, we can develop a post-state-diff fraud proof to resolve the dispute on-chain.
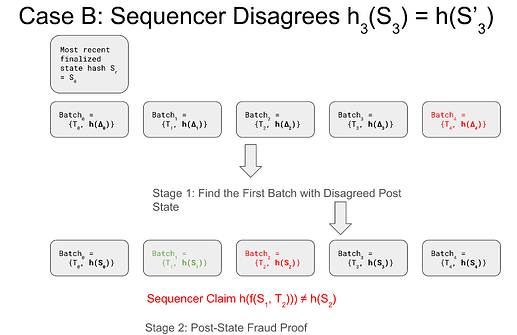
Case B: Sequencer Disagrees h(S'_{n-1})
When the sequencer disagrees the post state of batch n-1 from the challenger h(S'_{n-1}), we will perform a two stage fraud proof
- First, find the first batch of disagreed post states;
- Second, perform post-state fraud proof.
Stage One: Find the First Batch of Disagreed Post States
The first stage of the fraud proof dispute game will find the batch index x, r < x \leq n, such that
- the post state hash of the sequencer provided h(S_x) differs from that of the challenger h(S'_x), where S'_x is post state of batch x of the challenger;
- the previous post state hash of the sequencer h(S_{x-1}) equals to that of the challenger h(S'_{x-1}).
Similar to the traditional fraud-proof dispute game, this can be done in \log(n - r) time by performing an interactive dispute game. Note that a new state hash S_r can be also periodically updated (with a much longer submission interval) and finalized via the same optimistic mechanism.
Stage Two: Post-State Fraud Proof Case A
Given the batch index x with h(S_{x-1}) = h(S'_{x-1}) and h(S_{x}) \neq h(S'_{x}), the challenger claim reduces to
h(f(S_{x-1}, T_x)) \neq h(S_x)
We can apply existing fraud proof algorithms that current optimistic rollups have developed. Note that this stage can be accelerated by zk Fraud Proof .
Conclusion
In this article, we propose an acceleration of L2 execution by using flat KV storage for the state and replacing the hash of the post-state with the hash of the post-state diff in the on-chain batches. If the hash of the post-state diff is incorrect, we further propose a two-stage fraud-proof algorithm to dispute the wrong result by any challenger.