Here is an approach that extends the ideas of pointproofs towards:
- variable and unbounded growing of contract storage sizes,
- unbounded growing of the world state, and
- more importantly for validating clients to maintain only one commitment,
with having small witnesses containing:
- world state point proof,
- contract Storage point proof,
- relevant commitments for world state validation,
- relevant commitments of contract storage data validation.
A detailed version of the following write-up is available here: Adapting Pointproofs for Witness Compression - HackMD
Proposal
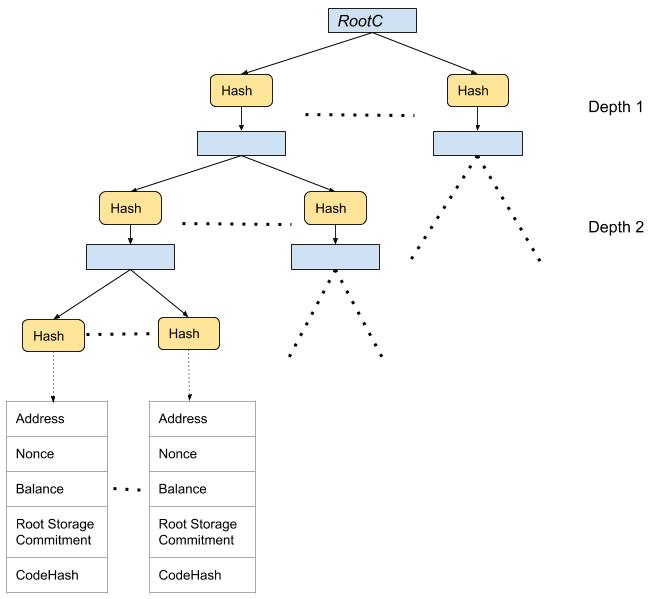
The core idea is to build vector commitments trees (VCTs) for the world state (shown below) and for contract storages.
At the very bottom, we have 32 byte hashes of the account information: address, nonce, balance, root storage commitment (discussed later) and codehash. N of such hashes are committed by a depth 2 vector commitment, that are hashed again and N of such hashes are bound by a depth 1 commitment, and are hashed yet again, and N of such hashes are bound by the root vector commitment, shown by RootC. When N = 1000, the RootC binds 10^9 accounts with a depth of 2. Note that this VCT does not store the account information, it only stores the hashes of them.
A validator needs to store only the world state root commitment. To verify, a stateless client needs to be provided with the read witness containing:
- positions of the accessed accounts,
- information of the accessed accounts,
- involved commitments, and
- the point proof \pi.
We need to fix an order to traverse this VCT. Any fixed traversal order such as in-order traversal is fine. We can then verify the cross-commitment aggregated proof using the same equation provided in the paper.
The number of required commitments inside the read witness for a block reading k accounts is in the order of k~log~k (logarithm base is N) in the worst case. Note that the size of Merkle proofs are in the order of the state size.
In addition to the above 1. to 4., updating accounts require just the updated account information. Adding an account is straight forward. The figure below shows the edge case when adding an account requires adding a level to the world state VCT.
The deletion of contract accounts can be achieved by updating the corresponding hash of the account to zeros. Note that we treat elements with all zeros to be empty accounts, or empty commitments.
Implementation detail / optimisation: It will save the number of exponentiations both for the prover and for the verifier if we allow Hash(0) to be 0.
The same concept of VCTs can be extended to contract storage also.
Advantages
- Witness compression. It can be seen that the number of relevant commitments needed is in O(k~log~k) where k is the number of accessed accounts in world state (correspondingly number of storage locations accessed in contract storage) and the logarithm is to the base N. In contrast, Merkle tree based proofs are in the order of the state size (correspondingly contract storage size). So, if a block accesses n accounts and k contract storage locations, we would need a witness, whose size in the order of O(n~log~n+k~log~k)
- Validator stores only one world state root commitment.
- One-time common trusted setup. Addition and deletion of accounts or the growth in contract storages do not require revisiting of the trusted setup. The public parameters obtained from the trusted setup for the world state and for the contract storages are the same and stay unchanged for the life of the block chain.
- Enables cache-friendly efficient implementation of World State and Contract Storage. Because VCTs do not need to store the account information or the contract storage data values. They store only the hashes and commitments. An independent implementation of these storages without hashes, enables faster access because of locality that can be exploited with caches.
Disadvantages
No exclusion proofs. Hence this approach is not applicable for data availability and accumulator problems.
Thanks to Olivier Bégassat (PegaSys, ConsenSys) for reviews and inputs.