Authors: @gyllone @Madao-3 @xiangxiecrypto
1. Introduction
Blockchain privacy and regulatory compliance are experiencing a dynamic shift, significantly inspired by the pivotal works of @vbuterin and @ameensol, their insightful paper, Blockchain Privacy and Regulatory Compliance: Towards a Practical Equilibrium along with the enlightening forum post on permissioned privacy pools, has laid a foundational framework for understanding the intricate balance between maintaining transactional privacy and adhering to regulatory norms. These resources delve deeply into the challenges and viable solutions for synchronizing privacy with compliance in the ever-evolving blockchain landscape.
A key takeaway from their works is the concept of ‘honest address sets’ which profoundly influences our approach to achieving a second-generation privacy protocol. In this framework, Association Set Providers (ASPs) emerge as crucial facilitators of credit within the zk-credit system, offering a structured approach to assess and attest to the creditworthiness of users. Meanwhile, membership proof ensures that all participants in a transaction are part of an honest address set, enhancing the security of our protocol and providing a safer, more trustworthy environment for users.
In summary, the works of Buterin and Soleimani have been instrumental in guiding our approach to developing a blockchain system that upholds both privacy and regulatory compliance. By integrating these concepts into our system, we have been able to create a more secure, efficient, and privacy-preserving second-generation protocol.
2. Components
2.1 Infrastructure
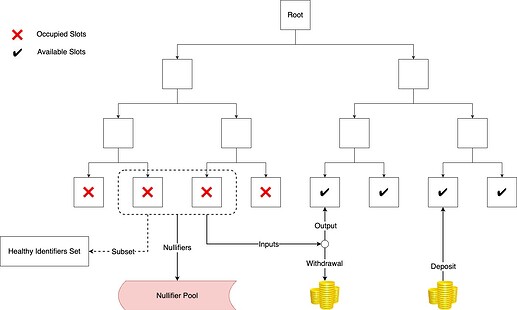
Users’ fungible assets are hashed into a Sparse Binary Merkle Tree. Suppose leaf node is initialized with a constant value H'=\mathrm{Hash}(0) until any asset occupies the slot of the leaf, then the leaf node should be updated to H=\mathrm{Hash}(identifier \ | \ amount \ | \ commitment), where identifier is an associated tag of this asset (e.g. the user’s address), amount is the quantity of the asset stored at the leaf node, and commitment = \mathrm{Hash}(secret), with secret being the key of the user who owns the asset.
For an unused leaf node slot, the user can deposit an asset into the pool and take the slot while providing the asset and commitment. For withdrawal, the user should provide the withdrawal amount, new leaf hash, identifiers subset, and the snark proof.
2.2 Proof of UTXO
The design of the withdrawal mechanism is similar to UTXO model. Users select a set of leaf nodes that indicate their assets to use as inputs, then hash the remaining balance into a new leaf node as output. The difference between the total input and the output is the amount of the withdrawal.
Now let the ULO source list be L, for each ULO with an index i\in L, we must first verify its existence and then calculate the corresponding leaf’s nullifier within the circuit as follows:
Next, we need to demonstrate that the total input amount is equal to the total output amount within the circuit, and then generate the leaf output. The following equations represent this:
Where amount_w is the withdrawal amount, amount_o is the output amount.
In the above process, we set \{nullifier_i\}_{i\in L}, leaf, root and amount_w as public variables of the circuit, which is constructed by Plonk.
2.3 Proof of Innocence
2.3.1 Why not Merkle proof
Proof of Innocence in ZKT Network lies in demonstrating that the inputs come from an arbitrary set constructed by the user, meanwhile ensuring that this set is publicly available to anyone. Typically, the set can be organized into a new Merkle Tree and the user should prove that each input is also a leaf node of the Merkle Tree (Indeed, privacy-focused solutions like Tornado Cash v2, and Privacy Pools have adopted this kind of design).
Apparently, if the set is small, the user’s privacy is compromised. If the set is too large, generating the corresponding Merkle tree incurs a huge gas cost on EVM, since ZK-friendly hash functions (Poseidon Hash) are not integrated by EVM primitively while creating Merkle tree has a complexity of O(n) hash.
We hereby adopt the Plookup to construct proof of membership, instead of Merkle Proof. There are 2 main advantages of Plookup in our membership proof.
-
In the proving phase, we do not need to perform merkle proof for each ULO, which significantly reduces the circuit size.
-
In the verification phase, we do not need to perform hash operations in EVM. Only one elliptic curve pairing is required.
2.3.2 Plookup embedding
Assuming the user provides an identifier set of size m from the source ULOs, denoted as \mathbf{t}, then we pad the set \mathbf{t} with 0 until it satisfies the size of circuit size n.
Furthermore, we define \mathbf{q_T}, which satisfy q_{Ti}\cdot t_i = 0:
Let \mathbf{f} be the query table:
Where c_i is the output witness defined in arithmetic gate of Plonk, we activate it when c_i represents the identifier witness. q_{Ki} is the selector that switches on/off the lookup gate.
Then we just need to prove \mathbf{f} is a subset of \mathbf{t}, by Plookup.
During the verification phase, besides the zk-SNARK proof verification, we also verify the opening proof of \mathbf{t} at \{1, \omega, \omega^2, ..., \omega^{m-1}\} to confirm the correctness of each identifier in \mathbf{t}, without any hash operations.
3. Association Set Provider
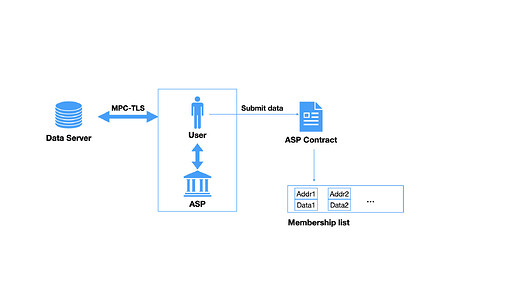
The Association Set Provider (ASP) mechanism allows a third party to oversee the membership list. Similar to an attestor, an ASP offers attestation services for end-users. The associated address, along with potential attested and sealed data, is submitted to a designated ASP smart contract. In ZKT Network, any entity can register as an ASP. The selection of which ASP to utilize depends on the choices made by end-users and Dapps.
The data category can be defined by the ASP, allowing support for a diverse range of potential data from web2, such as credit scores, KYC results, etc. For attesting any data obtained through the standard Transport Layer Security (TLS) protocol (e.g, HTTPS) and to accommodate a large volume of potential data, we recommend employing MPC-TLS style algorithms within the ASP. This approach, initially introduced by DECO and significantly improved by PADO, is detailed further in this paper. Within this framework, users can prove to the attestor that the data indeed originates from the intended sources without leaking any other information.
We list the basic workflow in the following figure.
The inclusion of data in the membership list is discretionary. This flexibility arises from situations where the data entry might simply be binary (YES/NO). In such cases, the smart contract accepts addresses marked as YES, allowing the omission of unnecessary data entries. However, programmability can be introduced when the sealed data holds additional meanings. For instance, an ASP might attest a user’s FICO score and store the encrypted score in the smart contract. Subsequently, Dapps can devise more adaptable withdrawal conditions. For example, users with higher FICO scores may be eligible to withdraw a larger quantity of tokens, whereas those with lower FICO scores might have access to only a smaller amount. This introduces a higher degree of flexibility for designing diverse applications.
4. Client-Side Acceleration Solution
In our quest to enhance user experience and efficiency in the ZKT Network system, we’ve focused on client-side computational optimization. This optimization is crucial for reducing the computational burden on user devices and accelerating transaction and verification processes.
4.1 WebAssembly Integration
Our integration of WebAssembly (Wasm) allows for the execution of complex cryptographic proof generation processes directly in the user’s browser. By compiling our Rust code into WebAssembly, we’ve significantly reduced dependency on centralized servers and improved system responsiveness and efficiency.
4.2 Local Computation Optimization
4.2.1 Transaction Decision Logic
In our UTXO model, each user’s funds are represented as encrypted NOTES, each corresponding to a specific amount of assets (e.g., ETH). Our system intelligently selects the appropriate combination of NOTES to fulfill withdrawal requests. For instance, if a user has NOTES of 1 ETH, 1 ETH, 2 ETH, and 3 ETH and wishes to withdraw 2.5 ETH, our system automatically utilizes the 1 ETH, 1 ETH, and 2 ETH NOTES.
4.2.2 Generation of New Deposit Proofs
Following the utilization of certain NOTES for transactions, our system generates new deposit proofs corresponding to the remaining amount. Continuing the previous example, after spending the 1 ETH, 1 ETH, and 2 ETH NOTES, a new deposit proof for 1.5 ETH is created, ensuring secure and effective management of funds post-transaction.
4.2.3 Implementation in Chrome Plugin and iOS App
To achieve this computational optimization, we’ve implemented tailored strategies in our Chrome plugin and iOS app. The Chrome plugin optimizes the NOTE selection and new proof generation process, leveraging the browser’s processing capabilities. In contrast, our iOS app employs multi-threading technology to accelerate these computations, taking full advantage of the high-performance capabilities of iOS devices.
4.3 Caching Strategies
We have implemented caching strategies to reduce redundant computations and network requests. Key data, such as parts of the Merkle Tree, are cached on the user device for quick retrieval in subsequent transactions or verifications, reducing network traffic and significantly enhancing overall system performance.
4.4 User Experience Enhancement
Lastly, we place a high emphasis on enhancing the user experience. This involves not only technical optimizations but also improvements in interface design. We ensure that the user interface is intuitive and the transaction process is seamless. Real-time feedback and detailed error messages enhance user trust and satisfaction.
In summary, our client-side acceleration solution is a key strategy for enhancing the performance of the ZKT Network system. Through these technological and methodological applications, we not only enhance the speed and efficiency of transactions but also optimize the user experience, making ZKT Network a more powerful and user-friendly blockchain privacy platform.
5. What does it mean?
At ZKT Network, we’re dedicated to realizing a grand vision: leading a technological revolution by balancing blockchain transaction privacy with global compliance standards. Our innovation extends beyond technical realms, exploring new frontiers in the balance of privacy and compliance.
Therefore, we warmly invite researchers and experts in the blockchain field to participate in our project, offering feedback and suggestions to advance this sector. ZKT Network looks forward to your professional insights and collaboration to develop a more comprehensive and effective blockchain privacy solution.
We also encourage community members to explore innovative applications based on our framework, as per their requirements. ZKT Network is eager to imagine the future with you, face challenges together, and build a more secure, compliant, and innovative blockchain world.
At ZKT Network, we believe that through collective wisdom and collaborative effort, we can achieve a perfect integration of privacy protection and compliance, creating a future filled with possibilities.
6. Summary
This post thoroughly explores the approaches and practices for achieving a balance between privacy protection and regulatory compliance in blockchain technology. By incorporating innovative applications of honest address sets, zk-credit, and membership proof, we demonstrate how to maintain user privacy while adhering to regulatory standards. The focus extends beyond the technical and system architecture to include engineering practices and enhancements in user experience performance. Our aim is to establish a secure, efficient blockchain system that delivers an exceptional user experience. Representing a step forward, this second-generation privacy transaction protocol signifies a better tomorrow, where privacy is not just a feature – it’s the norm.
Note: For more detailed proofs and information on the Plonk-related aspects mentioned in this article, please visit our GitHub page: papers/Advancing Blockchain Transaction Privacy and Compliance: Insights into Innovative Engineering Practices at main · ZKTNetwork/papers · GitHub.