AirScript: language for defining zk-STARKs

[vbuterin]

The nonce would be included in the proof, and the threshold parameter could be configurable. Also, I’m guessing this technique could be applied to the main Merkle tree ( mTree ) and Merkle trees in the FRI proof - right?

Yep! That looks correct to me.

As I was writing this, another potential optimization idea came to mind:

I’ve thought of this myself, and didn’t do it because it would make the code too complex and I was deliberately making mimc_stark.py an educational implementation rather than something crazy optimized. I have no idea whether or not this is secure; I’d recommend asking Eli.

Another thing worth exploring is playing around with making the FRI skip-down degree 8 instead of 4. The reason why this could be an optimization is that the Merkle tree (at least in mimc_stark.py) is designed in such a way that the FRI check values are right beside each other, so you only pay an O(1) cost for each value, plus O(log(N)) per sample for the branch. Making the skip-down degree 8 cuts down the number of sampling rounds by a factor of log(4)/log(8) (ie. by a third), at the cost of 2x more chunks, but that still seems like a net improvement.

[bobbinth]

I am wondering, would it make more sense to use a VDF instead of adding proof-of-work to Merkle roots? It could work like this:

1. Build a Merkle tree.
2. Compute seed = VDF(root, steps).
3. Generated indexes using the seed and PRNG.

The reasoning is as follows:

• 2^{20} proof-of-work takes about 1 second to compute on my computer. But someone with a modern ASIC could compute thousands (or even millions) 2^{20} proof-of-works per second.
• At the same time, running something like a reverse MiMC on my computer for 2^{16} steps takes about a second as well. But running thousands (or millions) of reverse MiMC calculations per second would take orders of magnitude more resources than buying an ASIC.

Are there any drawbacks of the VDF approach described above that I’m not seeing?

[vbuterin]

The problem is that you’re not really taking advantage of the VDF’s non-parallelizability, because the VDF could be calculated in parallel for many different choices of root. So it reduces to just being a hash function.

[bobbinth]

Yep, that makes sense. Though, even if it reduces to being just a hash function, I think using MiMC has some advantages. The biggest drawback is probably potential attacks against MiMC that we don’t need to worry about with true and tested hash functions.

---

There is another potential optimization I thought of which, if works, can reduce proof size by about 15%. The optimization tries to take advantage of some redundancies in the FRI proof structure.

In your example, each layer of a FRI proof contains two sets of Merkle paths (code):

1. Merkle paths for indexes in the “column” (tree m2 in the example);
2. Merkle paths for indexes in the “polynomials” (tree m in the example).

In subsequent layers, m2 becomes m, and a new m2 is created from m by splitting it into sets of quartic polynimials and evaluating them at a random point x. I tried to illustrate this in the graphic below:

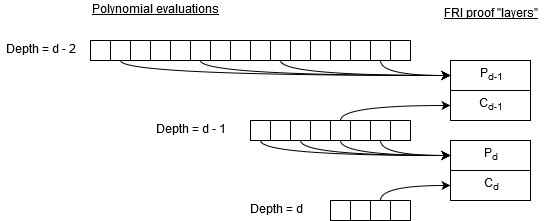
In this picture, P are the “polynomial” Merkle paths, and C are the “column” Merkle paths. For each path in C, there are 4 paths in P (in the example, number of paths in C is 40, and, thus, number of paths in P is 160).

It is easy to see that P_d and C_{d-1} paths come from the same tree. If we can make it so that C_{d-1} is a subset of P_d without compromising security, we can reduce FRI proof size by up to 20%. Here is how I think it could work:

Instead of deriving pseudo-random indexes from roots of m2 at every layer (code), we can do the following:

1. Derive pseudo-random indexes from the root of m2 at the last layer (i.e. depth d). These indexes will determine paths for C_d (40 indexes).
2. Use these indexes to determine indexes for P_d (160 indexes). This is done in the same way as now (code).
3. Use root of m2 at the next layer up to randomly sample indexes for C_{d-1} from P_d (basically, choose 40 random indexes out of the set of 160 indexes).
4. Same as in step 2, use indexes for C_{d-1} to determine indexes for P_{d-1}.
5. Move to the next layer up and repeat steps 3 and 4.

Here is an illustration of how indexes for each set of paths could be derived:

Basically, we recurse all the way down, and then use the root of the Merkle tree at the bottom layer to derive all other indexes as we move back up in the recursion.

It doesn’t seem like an attacker gains any advantages in this setup. They still need to build all the same Merkle trees on the way down in the recursion, and the indexes for each proof layer are still selected pseudo-randomly based on the roots of all treesn

If you (or anyone else), sees any flaws in this approach, let me know.

[bobbinth]

I’ve just released a new version of the library (v0.5.4) which has a bunch of speed and some proof size optimizations. The updated benchmarks are here, but at the high level, proof sizes went down a lot without impacting proof generation time. For example, a STARK for a Merkle proof of depth 16 (using Rescue hash function) is now ~63 KB and still takes about 1 second to generate.

To reduce the proof size, here is what I’ve done:

• Increased extension (or blow-up) factor from 8x to 16x, and reduced query counts to 48 for the execution trace tree, and to 24 for FRI proof trees. If I’ve done my math correctly, the resulting proofs have security level around 96 bits.
• In FRI proofs, packed all 4 elements of a single “row” into a single Merkle leaf (in the original code, each “row” element was put into a separate leaf). As far as I can tell, this doesn’t affect security, and I think StarkWare guys are doing the same thing (based on “FRI Layer Skipping” section from here).
• I have not yet added proof-of-work to Merkle roots. Doing so, will increase the security level to ~120 bits.

Proof size can probably be reduced further by 10% - 20% by implementing DEEP-FRI, and maybe even more if the approach I described in the previous post works.

To improve proof generation time, here is what I’ve done:

• Used latest version of Galois library. This improved speed of arithmetic operations in 128-bit fields by 8x - 9x.
• Implemented Blake2s hash function in WebAssembly. For small inputs (e.g. 32 - 64 bytes) it came out to be 4x faster than Node’s native implementation.
• Used a smaller domain for constraint evaluation. For example, if extension factor is 16x and constraint degree is 3, the constraints are evaluated in the domain that is 4x of the execution trace, and then the result is extended to the full 16x domain.

The performance is now approaching the limits of what can be done in a single thread - so, one of the future steps would be to update the library to make use of multi-threading.

[vbuterin]

Truly excellent work!

[denett]

I think your optimization works and is even a security improvement over the original, because it avoids the attack I have described here. I think it is quite similar to what I proposed at the end of that post. I proposed to follow the path in the forward direction and you are doing it in the reverse direction.

You can find some extra optimizations in my followup post here that you might be able to use.

[denett]

I have been thinking about it some more and I think this part could be problematic:

Use root of m2 at the next layer up to randomly sample indexes for C_{d−1} from P_d (basically, choose 40 random indexes out of the set of 160 indexes).

An attacker could try to influence which indexes are chosen by trying multiple versions of the tree. The attacker could try to do this again at every level of the recursion, thus greatly increasing the odds that the attack succeeds.

I think it would be better to use the combined hash of all roots as the random source to pick the indexes at every step. Now you only have to add the PoW to this random source instead of to all the tree roots.

[bobbinth]

Thank you for thinking about this! I’m by no means an expert on these subjects, but here are my thoughts:

Regarding your first comment: I’m not sure I see how the scheme I proposed or the scheme you proposed here can increase security. It seems to me that both schemes make it more difficult to cheat at several layers simultaneously, but they don’t make it any more difficult to cheat at any given layer. I guess the question is, if you are able to cheat in a single layer, does this compromise the entire proof or do you need to cheat at more than one layer? If the former, then at best, the security stays the same.

Regarding other optimizations you mention here:

1. Already implemented - reduced proof size by quite a bit.
2. This could be significant too - though it’s quite a bit of work (primarily because I’d need to write optimized versions of octic polynomial evaluation/interpolation functions - otherwise proving time would suffer quite a bit).
3. I’m not sure the benefit here would be meaningful. Yes, we could send fewer than 256 values, but then we’d have to send Merkle branches for the values that we do send. This probably would offset the savings quite a bit - so, net savings are unlikely to be more than 1% of proof size, and potentially less than that.
4. I’m not sure I fully understood this. Is the suggestion to increase the number of last layer values beyond 256? If so, I think it could result in some savings - but I’ll need to think more about the exact benefit.

Regarding your last comment: the only tree the attacker would manipulate to influence the choice of indexes is the base layer tree (tree at depth d). All other trees are “fixed” - meaning, if you change any of them, you’d be changing the base layer tree too (so, it’s probably easier to manipulate the base tree directly).

One of the open questions in mind is: does my scheme make it somehow easier for the attacker to build trees at each layer in such a way that the probability of cheating at any one layer increases.

[denett]

I will explain in more detail how we can do an attack on the original version.

I assume that it possible to cheat on a large majority of the constraints except that the values that go into the FRI are not on a low degree polynomial. So we have 16X values that are supposed to be on a X degree polynomial, but are actually on a 16X degree polynomial. If we build the FRI proof with these values we will get caught at the final step because the 256 final values are not on a 16 degree polynomial, but are on a 256 degree polynomial.

The FRI proof is organized in such a way that we can separate the 16X values into 256 groups. Each group of values are used to calculate one of the 256 final values. These groups are independent in the sense that we can change the values in one group, without causing checks in other groups to fail. Changing values in one group will off-course change which rows/columns are chosen, but all checks on all untouched groups will pass. If we only change the values of a group at one stage of the recursion then that will only cause the checks to fail if a row from that group is chosen at that specific stage of the recursion. They will all pass at every other stage.

To cheat on the FRY we will pick 16 groups with a total of X values and determine what the values in all other groups need to be if they were on the same polynomial as the chosen X. This is our target polynomial. Note that if we would use the target polynomial to start the FRI, we would pass the check on the final 256 values, but it is unlikely that we would pass the first checks, because we have changed 15X of the 16X values. So instead of changing 15X values we will only change a few groups at the first step of the recursion to the target polynomial. Since only a small percentage of the values have changed we have a pretty good chance of not to get caught.

If we change 24 groups and do 40 checks we have a ((256-24)/256)^{40} = 1.9\% chance to pass all checks. We do not have to try many variations of the tree to get away with it.
After we found a solution that passes all checks, we will go to the next level of the recursion and we will change another 24 groups. After 10 recursions all groups are on the same low degree polynomial and we will pass the check on the 256 values.

It is easy to see that our proposals are not vulnerable to this attack, because we will always check at every stage of the recursion and we will spot any changes made.

The attack on your proposal is different but is based on the same principle: Try many variations of the tree and use the best one to go to the next level of the recursion.

It depends on the implementation, but the 160 values from which 40 are chosen are probably ordered in a specific way. In a basic implementation every set of four values come from the same row and are ordered from low to high. Knowing this, we could try many variations of the tree and choose the tree that would pick as many low values a possible. Having done this at every level of the recursion, some values are far more likely to be checked than others. If we chose our X values to be the ones that are found via a path of mainly low values we are more likely to pass all checks.

Regarding optimization 3. The idea is to not publish the 256 values or any merkle branches.
The 40 final values are calculated based on 160 values of the level below and the chosen column.
These 40 final values are supposed to be on a 16 degree polynomial, so we only check if that is the case. This could lower the security of the proof a little because we will accept any 16 degree polynomial, but I don’t think it would help an attacker a lot to be able to use multiple polynomials in the final stage that are not to be mixed.

Regarding optimization 4. The idea is to use more values at the start of the FRY proof (like 32X instead of 16X) and less checks per level of recursion, but as I read above, you have already considered that.