Below is a more detailed explanation of how the current version of genSTARK library works on the example of a Merkle proof computation.
Library components
First, I want to briefly describe all the components that come into play to when generating/verifying STARK proofs (a more in-depth explanation is here and here). Here is a high level diagram of how proofs can be generated:
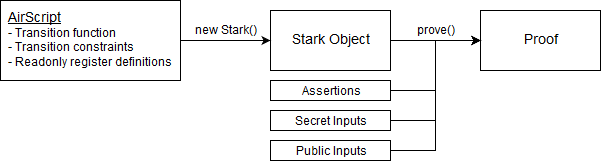
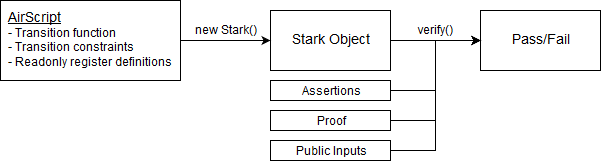
In the above diagram:
-
AirScript code defines transition function, transition constraints, and readonly registers. This code is then “compiled” into a Stark object.
-
Stark object is used to generate proofs. You can generate many proofs using the same Stark object by providing different assertions (same as boundary constraints), secret and/or public inputs.
Verification of a proof works in a similar manner, except the verifier does not need to supply secret inputs to the verify() method:
Merkle Proof
Let’s say we have a Merkle tree that looks like this (numbers in the circles are values of the nodes):
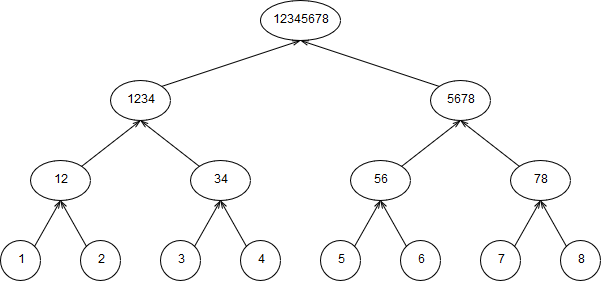
For illustrative purposes I’m assuming that hash(a,b) = ab. For example, hash(3,4) = 34 and hash(4,3) = 43.
A Merkle proof for leaf with index 2 (node with value 3) would be [3, 4, 12, 5678]. To verify this proof we need to do the following:
- Hash the first two elements of the proof:
hash(3,4) = 34
- Hash the result with the next element of the proof:
hash(12,34) = 1234
- Hash the result with the next element of the proof but now the result should be the first argument:
hash(1234, 5678) = 12345678
Execution Trace
Now, let’s translate the above logic into an execution trace that we can later convert into a STARK proof.
First, let’s say we have a hash function that works like this:
- The function requires 4 registers to work and takes exactly 31 steps to complete.
- To hash 2 values with this function, we need to put the first value into register 1 and the second value into register 2 (the other 2 registers can be set to
0).
- After 31 steps, the result of hashing 2 values will be in register 1.
Our execution trace will have 8 mutable registers - 4 registers for computing hash(a,b) and the other 4 registers for computing hash(b,a). These registers are named r0 - r7. We also need a few readonly registers:
-
k0 - this register will control transition between invocations of the hash function.
-
p0 - this is public input register that will contain a binary representation of the index of the node for which the Merkle proof was generated. In our case, the index is 2 so the binary representation is 010.
-
s0 - this is a secret input register that will contain elements of the proof.
Now, since we need to invoke the hash function 3 times, and we need a step between each invocation to figure out which values to hash next, our execution trace will have exactly 96 steps (for the purposes of this example I’m not requiring the trace length to be a power of 2):
| Step |
k0 |
p0 |
s0 |
r0 |
r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
r7 |
| 0 |
1 |
0 |
12 |
3 |
4 |
0 |
0 |
4 |
3 |
0 |
0 |
| … |
1 |
0 |
12 |
… |
… |
… |
… |
… |
… |
… |
… |
| 31 |
0 |
0 |
12 |
34 |
… |
… |
… |
43 |
… |
… |
… |
| 32 |
1 |
1 |
5678 |
34 |
12 |
0 |
0 |
12 |
34 |
0 |
0 |
| … |
1 |
1 |
5678 |
… |
… |
… |
… |
… |
… |
… |
… |
| 63 |
0 |
1 |
5678 |
3412 |
… |
… |
… |
1234 |
… |
… |
… |
| 64 |
1 |
0 |
… |
1234 |
5678 |
0 |
0 |
5687 |
1234 |
0 |
0 |
| … |
1 |
0 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
| 95 |
0 |
0 |
… |
12345678 |
… |
… |
… |
56781234 |
… |
… |
… |
Here is what’s going on:
- [step 0]: we initialize registers
r0 - r7 as follows:
a. First element of the proof (3) is copied to registers r0 and r5.
b. Second element of the proof (4) is copied to registers r1 and r4
c. All other mutable registers are set to 0
- [step 31]: after 31 steps, the results of
hash(3,4) and hash(4,3) are in registers r0 and r4 respectively. Now, based on the value in register p0 we decide which of the hashes advances to the next step. The logic is as follows: if p0=0, move the value of register r0 to registers r0 and r5 for the next step. Otherwise, move the value of register r4 to registers r0 and r5.
a. In our case, at step 31 p0=0, so the value 34 moves into registers r0 and r5 for step 32.
- [also step 31]: At the same time as we populate registers
r0 and r5 with data for the next step, we also populate registers r1 and r4 with data for the next step. In case of r1 and r4, these registers are populated with values of register s0 which holds the next Merkle proof element.
a. In our case at step 31 value of s0=12, so 12 moves into registers r1 and r4 for step 32.
- After this, the cycle repeats until we get to step 95. At this step, the result of the proof should be in register
r0.
In my prior posts I’ve shown an AirScript transition function that would generate such a trace. Here is a simplified version:
when ($k0) {
// code of the hash function goes here
}
else {
// this happens at steps 31 and 63 (technically at step 95 as well, but doesn't matter)
// select the hash to move to the next step
h: $p0 ? $r4 | $r0;
// value h goes into registers r0 and r5
// value from s0 goes into registers r1 and r4
out: [h, $s0, 0, 0, $s0, h, 0, 0];
}
And here is how transition constraints for this would be written in AirScript:
when ($k0) {
// code of the hash function constraints goes here
}
else {
h: $p0 ? $r4 | $r0;
S: [h, $s0, 0, 0, $s0, h, 0, 0];
// vector N holds register values of the next step of computation
N: [$n0, $n1, $n2, $n3, $n4, $n5, $n6, $n7];
// this performs element-wise subtraction between vectors N and S
out: N - S;
}
Readonly registers
A bit more info on how values for readonly registers (k0, p0, s0) are set:
As I described previously, k0 is just a repeating sequence of 31 ones followed by 1 zero. It works pretty much the same way as round constants work in your MiMC example. Within AirScript k0 is considered to be a static register are the values for this register are always the same.
Values for p0 are calculated using a degree n polynomial where n is the number of steps in the execution trace. The polynomial is computed by generating the sequence of desired values (e.g. for index 010 it would be 32 zeros, followed by 32 ones, followed by 32 zeros), and then interpolating them against lower-order roots of unity. Since the verifier needs to generate values for this register on their side as well, p0 register is considerably “heavier” as compared to k0 register. But for execution traces of less than 10K steps (or even 100K steps), the practical difference is negligible. Within AirScript, p0 is considered to be a public input register as its values need to be computed at the time of proof generation and verification and so must be known to both the prover and the verifier.
Values for s0 are computed in the same way as values for p0 but unlike p0 the source values are not shared with the verifier. Instead, values of s0 are included into the proof in the same way as values of mutable registers. From the verifier’s standpoint, s0 is almost like another mutable register, except the verifier does not know a transition relation for this register. The verifier is able to confirm that values of s0 form a degree n polynomial where n is the number of steps in the execution trace.
This is not really a problem given our transition function and constraints. Basically, what the verifier sees is that every 32 steps an unknown value is copied into registers r1 and r4, and then this value is used in hash function calculations that produce the desired output. Within AirScript, s0 is considered to be a secret input register as the verifier is not able to observe source values for this register.
Boundary constraints
The only boundary constraint that we need to check here is that at the end of the computation we get to the root of the Merkle tree. If everything worked out as expected, the root should be in registers r0 or r4 (depending on wither the index of the leaf node is even or odd).



