An Anti-Collusion Mechanism for Threshold Encrypted Mempools
Thanks to Luis Bezzenberger for valuable comments on this post.
TL;DR: Encrypted mempools are a promising approach to prevent the malicious extraction of maximal extractable value (MEV) in public blockchains such as Ethereum. Threshold encryption is a good candidate to establish an encrypted mempool, but unfortunately crucially relies on the threshold trust assumption: the assumption that within a predefined set of parties (the threshold committee) at least a subset of these parties act honestly. In this post, we explore an approach to establish a threshold encrypted mempool that remains secure even if all parties in the threshold committee collude.
Maximal Extractable Value (MEV) in blockchain networks describes the value that certain participants can capture by manipulating the transaction execution order, often at the expense of other users. Indeed, it is estimated that the total amount of MEV stolen from users in Ethereum to date ranges somewhere between 1.1 and 3 billion USD. Encrypted mempools are a promising approach to prevent malicious MEV extraction by encrypting transactions until their execution order is fixed. A good candidate for establishing an encrypted mempool is threshold encryption, which is a public key encryption scheme where the decryption key is split among a committee of parties. That is, in order to decrypt a ciphertext, collaboration from at least a certain threshold number of these parties is required. If fewer than this number of parties participate, no information about the plaintext or decryption key is revealed. This primitive enables an encrypted mempool as follows:
-
The threshold committee initially generates a public key and shares of the corresponding secret key.
-
Users encrypt their transactions with the public key of the threshold committee.
-
Once the position of an encrypted transaction is “fixed” at the top of a block, the committee jointly decrypts the ciphertext and reveals the transaction.
While threshold encryption is a promising approach, it relies on the threshold trust assumption - the premise that fewer than the threshold number of committee members act maliciously. If this threshold is exceeded, the malicious parties could collude to decrypt transactions prematurely, enabling them to learn the content of encrypted transactions and thereby to extract malicious MEV. In this post we explore an anti-collusion mechanism for threshold encrypted mempools that effectively reduces the threshold trust assumption. We illustrate the mechanism at the example of an encrypted mempool using the Shutter threshold encryption scheme and discuss later that it can be generalized to essentially any threshold encrypted mempool.
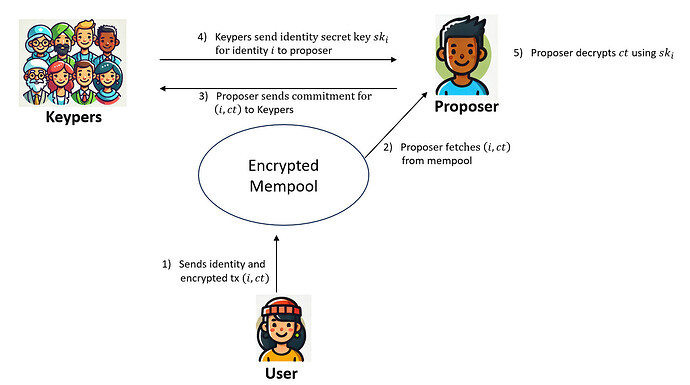
Recap: Shutter Encrypted Mempool
Shutter is essentially a threshold variant of the Boneh-Franklin identity-based encryption (IBE) scheme. An IBE scheme consists of a master public/secret key pair (mpk, msk) and it allows to encrypt a message m w.r.t. some identity i and the master public key mpk. In the following, we will denote the Shutter encryption by ct \leftarrow Shutter.Encrypt(mpk, i, m). The resulting ciphertext ct can be decrypted by deriving a so-called identity secret key sk_i from the master secret key msk and identity i and using sk_i for decryption. We denote decryption by m \leftarrow Shutter.Decrypt(sk_i, ct). Typically in IBE schemes the master secret key is maintained by a trusted authority, but in the case of Shutter it is distributed among a committee of parties, the so-called Keypers, such that no single party has access to the full key. That is, for a Shutter encrypted mempool, a user can send its transaction tx encrypted under mpk and an identity i. Then, once the position of the encrypted transaction is fixed at the top of a block, the Keypers jointly derive the identity secret key sk_i and decrypt the transaction.
What Does it Mean to Fix a Ciphertext’s Position in a Block?
MEV can only be prevented effectively by threshold encryption, if the position of a ciphertext in a block is fixed at the top before decryption. Otherwise the block proposer could simply wait for a ciphertext to be decrypted and re-order its execution based on its content. There are several ways to ensure a fixed position, such as inclusion lists like FOCIL or proposer commitments (see, e.g., Commit-Boost). In this post, we focus on a threshold encrypted mempool design that leverages proposer commitments — a concept we recently explored in detail here). Later, we will discuss how this approach could potentially be generalized to other methods of enforcing transaction order after decryption.
Proposer commitments allow a block proposer to make commitments on the allocation of space in the block it is about to propose. A popular use case of such commitments are transaction pre-confirmations, where the block proposer commits to including certain transactions into its block, thereby giving the transaction senders the assurance that their transactions will indeed be executed once the block is finalized. At a high level, proposer commitments are signed statements and if the proposer does not follow its commitment, it can get slashed thereby disincentivizing malicious behavior. Commit-Boost, a prominent standardization effort for proposer commitments, specifies that commitments can be for instance a BLS signature under the existing validator keys.
In the context of encrypted mempools, proposer commitments can be extended to include encrypted transactions. A proposer might commit to including a decrypted ciphertext in the block, provided the resulting transaction is valid. The commitment could be a signed statement “If ciphertext ct contains a valid transaction and if it is being decrypted on time, I will include the transaction encrypted in ct at the top of block k”.
The Anti-Collusion Mechanism
High Level Idea. The main idea of the anti-collusion mechanism is to make it technically infeasible for the Keypers to decrypt a ciphertext from the encrypted mempool before the block proposer has made a valid commitment to include the decrypted transaction at the top of the block. This ensures that if a ciphertext is decrypted, the resulting transaction will be included into the next block or the proposer will be slashed. If such a commitment does not exist, then the Keypers cannot decrypt the ciphertext. In the following, we describe this approach at a more technical level.
Technical Details. At the core of the anti-collusion mechanism is the following observation made by previous works (e.g., 1, 2): a BLS signature can be used as a decryption key in the Boneh-Franklin encryption scheme. Since Shutter is based on the Boneh-Franklin scheme, the same holds for Shutter. Let’s go into a bit more detail:
- BLS, as used in Ethereum, and Shutter operate over the same elliptic curve BLS12-381
- A BLS public and secret key pair can also be used as a master key pair for Shutter
- An identity secret key in Shutter has the structure of a BLS signature, i.e., the identity secret key for identity i is sk_i = H(i)^{msk} and sk_i is a valid BLS signature for i under secret key msk
All of this means that a BLS signature of a proposer can be used as a decryption key for Shutter.
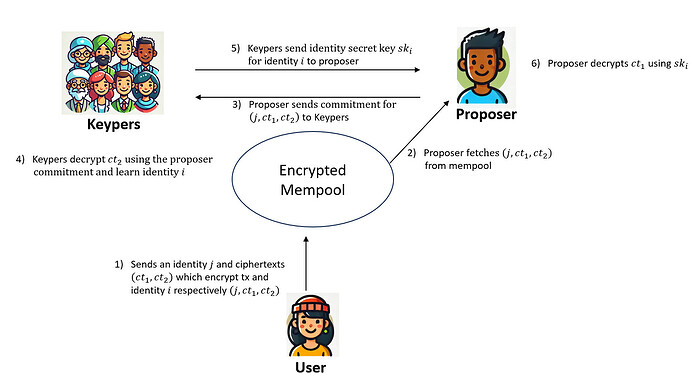
The anti-collusion mechanism then works as follows: Let mpk be the master public key of the Shutter committee and let pk be the BLS public key of the proposer. Then a user encrypts its transaction tx as follows:
- as before the user encrypts tx using mpk and an identity i, i.e., the user computes ct_1 \leftarrow Shutter.Encrypt(mpk, i, tx)
- in addition, the user encrypts i under pk and another identity j, i.e., the user additionally computes ct_2 \leftarrow Shutter.Encrypt(pk, j, i)
The user then sends both ciphertexts (ct_1, ct_2) along with identity j to the encrypted mempool. Note that without knowing identity i, the Keypers cannot decrypt ct_1 and therefore they cannot learn transaction tx. Eventually, the proposer commits to including tx at the top of its block by sending a BLS signature on identity j, i.e., \sigma = H(j)^{sk}. This signature is essentially the identity secret key for identity i and public key pk, i.e., it can be used to decrypt identity i by computing i \leftarrow Shutter.Decrypt(\sigma, ct_2). Now that identity i is known, the Keypers can decrypt the transaction tx by first deriving the identity secret key sk_i and then computing tx \leftarrow Shutter.Decrypt(sk_i,ct_1).
As long as the proposer and the Keypers do not collude, it is technically infeasible for the Keypers to decrypt tx before the proposer commits to including it. Note that decrypting tx after the proposer has sent its commitment causes no harm as the transaction is already committed to be included at the top of the block.
Discussion and Limitations of the Approach
Preventing collusion between Keypers and Proposer. The proposed mechanism mitigates the harmful effects of collusion within the threshold committee by ensuring that decryption is only possible once the current block proposer commits to including a decrypted ciphertext at the top of the next block. However, as mentioned above, this approach does not address potential collusion between the Keypers and the block proposer. To effectively disincentivize such collusion, it is essential to introduce economic penalties for both the committee of Keypers and the proposer in cases of misbehavior.
Encrypting to several proposers. Another limitation is that in its current form, a user always encrypts its transaction to a specific proposer. If this proposer does not commit to the transaction, it will not be included, essentially forcing the user to resend the transaction. An obvious countermeasure is to let the user encrypt towards several proposers to increase the likelihood of one of them actually committing to including the transaction. However, this comes with two drawbacks: (1) it increases the ciphertext size linearly in the number of proposers and (2) the more proposers are involved, the more likely it is that one of them would collude with the Keypers. The first drawback could be addressed by using a multi-recipient encryption scheme. The second drawback on the other hand seems to be more of a tradeoff between security and convenience: the more proposers the user chooses, the more likely the risk that one of them colludes with the Keypers, but the less likely it is that the user has to resend the transaction.
Ensuring that Keypers release the decryption key. If we assume that all Keypers act maliciously and collude with each other, there is the possibility that they refuse to release decryption keys, thereby bringing the system to a halt. A solution to avoid this is to have Keypers stake some funds and to have a committee of attesters attest to whether or not the Keypers released the decryption key for a valid proposer commitment. If the Keypers do not release the key, they risk having their stake slashed.
Why do we need Keypers if users can encrypt directly to the proposer? One might wonder, why we even need a committee of Keypers at all if proposer commitments allow users to encrypt their transactions directly to a proposer. The reason is that without the committee, a malicious proposer could just locally decrypt transactions without publicly committing to including them, thereby essentially opening the door for MEV attacks again. Only if there is another independent party (in our case a committee) that is required for decryption of the transaction can we force the proposer to make its commitment public and thereby make sure that the proposer is held accountable.
Ordering of encrypted transactions at the top of the block. Throughout this post, we’ve assumed that when a proposer commits to an encrypted transaction, the corresponding decrypted transaction must appear at the top of the block. But what happens if the proposer commits to multiple transactions? In that case, there is no clear ordering of these transactions.
A simple solution would be for the proposer to include an incrementing counter with each commitment. Transactions can then be ordered by this counter, and Keypers would only decrypt them in that sequence.
We note that this ordering issue does not arise when using inclusion lists instead of proposer commitments, since the inclusion list can explicitly define the ordering of encrypted transactions in the block.
Generalizing the Approach
There are two ways our approach can be generalized, namely w.r.t. the encrypted mempool and w.r.t. the mechanism of fixing a ciphertext’s position.
Generalizing the encrypted mempool. For simplicity, we described the anti-collusion mechanism w.r.t. a Shutter encrypted mempool. However, the core idea is independent of Shutter. The main insight is that a proposer commitment in form of a BLS signature can serve as a decryption key in the Boneh-Franklin IBE scheme. This can be combined with any (threshold) encrypted mempool using proposer commitments. Consider the following more general design: Let pk_C be the public key of the committee operating the (threshold) encrypted mempool and let pk_P be the proposer public key. Then a user can first encrypt its transaction to the encrypted mempool (i.e., under pk_C) and then encrypt the resulting ciphertext to the proposer via the Boneh-Frankling IBE scheme under pk_P. This essentially creates a doubly encrypted transaction that must first be decrypted by the proposer (through a commitment) and then the threshold committee can decrypt the transaction.
Generalizing the “fixing” mechanism. We described the anti-collusion mechanism for an encrypted mempool that uses proposer commitments to fix the position of a ciphertext in a block. However, at a more abstract level the mechanism is independent of the exact way of fixing the position as long as the fixing is done in the form of a BLS signature that can serve as a decryption key. For instance, for FOCIL the inclusion list could be signed with a BLS signature that allows to decrypt all transactions in the inclusion list. However, the exact integration of a mechanism like FOCIL with our anti-collusion solution remains an interesting task for future work.
Conclusion
The solution described in this post presents a practical and efficient anti-collusion mechanism for threshold encrypted mempools which could even be generalized to any kind of encrypted mempool. By tying decryption to proposer commitments (and potentially even inclusion lists), the mechanism significantly reduces trust in the encrypted mempool provider without requiring any large communication or computational overhead.