TLDR:
Justin’s BLS signature aggregation[1] aggregates the signatures in about 9 minutes.
In this post, we try to present a simple off-chain scheme based on the BLS aggregation in [1], which might reduce the aggregation time to about 12 seconds and therefore lead to reduce the finalization to <= 1 min.
The idea is that:
1.divide the validators into groups(called tribes), then divide the level-1 tribes in level-2 tribes, etc.
2.the tribes aggregate the signature from son-tribes, and only report it to its parent-tribe at some time intervals, so as to:
- spread the load of the signature aggregation to multiple nodes (which helps detect the invalid signatures)
- save the bandwidth
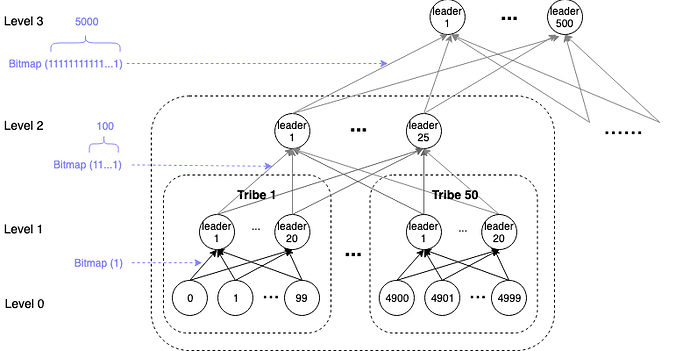
This is a diagrammatic sketch(3 level tribes and single leader per tribe):
Figure 1
Since I am still quite new to the Ethereum-related area, there might be a lot of stupid errors and even completely non-sense, please pardon me for that.
Assumption
- We have 312,500 validators, with id from 0 to 321,500 -1.
- We assume any validator can only receive 120k bytes at most per second(This is based on 4 messages/s on any connection between validators, each message is about 30k. We know in a peer-to-peer network, we don’t have direct connections between any two nodes, the streams have to share a common direct connection in many cases.I think it could be reasonable that the peak at any direct connection is about the same as the peak of the incoming to a node).
Bitmap
First we define a corresponding bitmap for a signature aggregation(which is also used in [1], but not described in detail).
Given an aggregation of the signatures from validators with id_0, id_1, ..., id_k, we define the bitmap like this:
- the bits of the bitmap are 1 at positions id_0, id_1, ..., id_k
- the others are 0.
E.g., the bitmap for validator 0 and 2’s aggregation is 101
Given bitmap A, B, we say:
- A includes B, iff A&B=B. E.g., 11 includes 10, 01 and 00.
- A is orthogonal with B, iff A&B=0. E.g., 10 and 01 are orthogonal.
- A conflicts with B, iff they don’t include each other, and they are not orthogonal. E.g., 011 and 110 conflicts.
- |A| is the count of 1s in A. E.g., |101|=2
The Scheme
It could be easy to demonstrate the scheme with a specific example, please check the figure blow:
Figure 2
Set up:
- Level 1:
Divide the 312,500 validators(as level-0) in 3,125 tribes(level-1 tribe). In each tribe there are 100 validators, the ids of which are consecutive. E.g., the ids in the first tribe are 0…99. In each level-1 tribe, select 20 validators as leaders. - Level 2:
Divide the 3,125 tribes in 63 level-2 tribes, each including 50 level-1 tribes(the last one is with 3125-62*50=25 level-1 tribes). Select 25 validators as leaders in each tribe. - Level 3:
Take all the 312,500 validators as one level-3 tribe, select 500 validators as leaders.
Aggregation:
- Level 0 → Level 1:
Validators sign the block and report to all the 20 leaders of the level-1 tribe which it belongs to:
- the signature
- the bitmap
-
Level 1-> Level 2:
Take 1s as one round. In each round, the leaders at level-1:
2.1. verify the signatures arrive in the round
2.2. aggregate the valid ones with the aggregation in last round
2.3. at the end of the round, report the aggregation with bitmap to the 25 leaders at level-2 -
Level 2 → Level 3:
Take every 9 seconds as a round, the leaders at level-2:
3.1 since the leader gets 20 aggregations from each one son-tribe, they may conflict with each other, the leader will select the aggregation A in each son-tribe, by:
1)A must include the aggregation from the tribe in last round.
2)if A includes B, select A
3)if A, B conflicts, if |A| >|B| select A, else B
3.2 similar to 2.2 and 2.3. verify the select ones, aggregate and report them to level-3 -
Level 3 → broadcast:
Take 1 second as a round, the leaders do the similar to 3, except they broadcast the signature(when they get >2/3 signatures).
Performance
First we need to know the size of the signature and bitmap. Since the ids in each tribe are consecutive, the bitmap can be represented in a segment of bitmap with start pos(2 bytes) and length(2 bytes). So if we have V validators in the tribe, the size is:
signature\ size + bitmap\ size =96 + (\lceil V/8 \rceil + 4)= \lceil V/8 \rceil + 100
level 0 → level 1:
CPU of validators:
I have no idea how much time to sign a message, I guess it is negligible.
Bandwidth:
Each validator reports: \lceil V/8 \rceil + 100=101 bytes, each leader receives |validators\ per\ level\ 1\ tribe| \times101= 100 \times 101 = 10,100 at most in a second(if all the validators send their signature in one second)
level 1 → level 2:
CPU of leaders at level-1:
T=|validators\ per \ level\ 1\ tribe| \times (T_{verify\ per\ v} + T_{aggregate\ signature\ per\ v})
Here, T_{verify\ per\ v}=2 \times T_{pairing} = 2\times 2.7ms = 5.4ms (please check post[1] as reference)
T_{aggregate\ signature\ per\ v}= 4,500ns
So, T=100\times (5.4ms+4,500ns)\approx 540ms
with quad-cores, it about 135ms.
Bandwidth:
Each leaders at level-1 reports: \lceil 100/8 \rceil + 100=113, each leader at level-2 receives:
|son\ tribes|\times |leaders\ per\ tribe|\times 113=50\times 20\times 113 = 113,000 bytes at most in a second
level 2 → level 3:
CPU of leaders at level-2:
T=T_{verify} + T_{aggregate\ signature}
T_{verify} =|level\ 1\ tribes\ per\ level\ 2\ tribe|\times T_{verify\ per\ tribe}
=50\times(T_{mul\ pub\ keys} + 2\times T_{pairing})
=50\times(|validators|\times T_{mul\ in\ G2}+ 2\times 2.7ms)
=50\times(100\times 1,350ns+2\times 2.7ms)= 276.75ms
T_{aggregate\ signature}=|level\ 1\ tribes\ per\ level\ 2\ tribe|\times T_{mul\ signatures}
=50\times 4,500ns=0.225ms
So, T\approx 277ms, with quad-cores, it is about 69.25ms.
Bandwidth:
Each leader at level-2 reports about:
R=\lceil |validators\ in\ level\ 2\ tribe|/8 \rceil + 100 bytes.
Each leader at level-3 receives: |level\ 2\ tribes| \times |leaders\ per\ level\ 2\ tribe| \times R\approx |leaders\ per\ level\ 2\ tribe|\times 312,500/8=25\times 312,500/8=976,562 bytes.
Since we have 10 seconds per interval, the bandwidth is about 108,506 B/s.
level 3 → broadcast:
CPU of leaders at level-3:
T=T_{verify} + T_{aggregate\ signature}
T_{verify} =|level\ 2\ tribes|\times T_{verify\ per\ tribe}
=63\times(T_{mul\ pub\ keys} + 2\times T_{pairing})
=63\times(|validators|\times T_{mul\ in\ G2}+ 2\times 2.7ms)
=63\times(50\times 100\times 1,350ns+2\times 2.7ms)=765.45ms
T_{aggregate\ signature}=|level\ 2\ tribes|\times T_{mul\ signatures}=63\times 4,500ns=0.2835ms
So, T\approx 766ms, with quad-cores, it is about 191.5ms.
Conclusion
If the assumptions are correct, we can aggregate the signatures in about 12s, if the blocks are broadcasted in 10s, the signature aggregations are broadcasted in about 10s, then we can finalize some block in about 32s(or justify it and finalize in next epoch in about 1 min)
Note
- To avoid the validators sending invalid signatures or aggregations, if we can request them to sign the aggregation, the leaders are able to find out those invalid, and submit them to slash the dishonest validators.
- This is just an example, we can adjust the parameters to get optimized result.