Introduction
Swap-or-Not is an SSLE technique designed by Buterin. Recall that SSLE aims to select W out of N validators in a fair and uniform way over the course of W shuffles of validators’ commitments, so that only the commitment owner knows his position in the final order.
Swap-or-Not
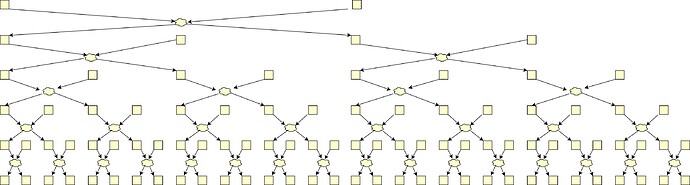
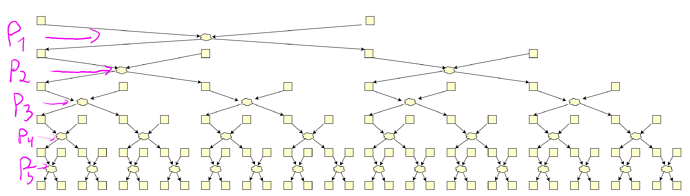
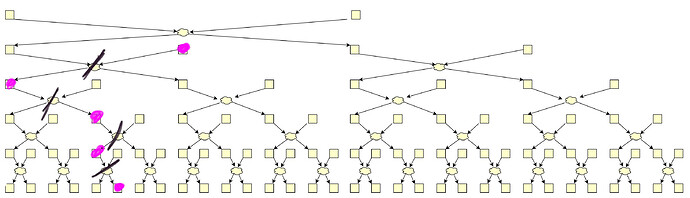
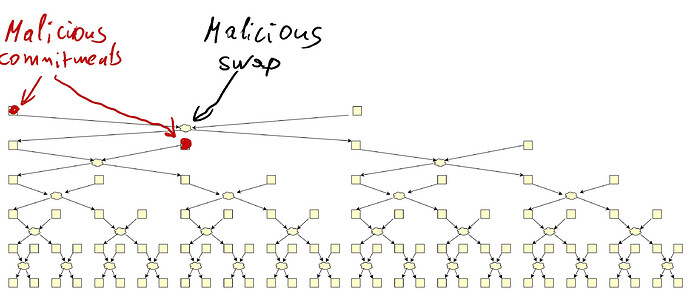
Swap-or-Not mixes 32 commitments per single stir using only secret swaps (i.e. mixes of 2). First, two positions are determined by a RANDAO call and secret swapped. The RANDAO usage ensures the positions are unknown in advance.
Then they are exchanged with two others, then with 4 others, and so on. The offsets of those positions are determined in the very first RANDAO call.
Therefore each of the first two commitments can end up in any of the 32 positions.
Each tree layer is handled by a different shuffler.
To mix better, trees run in parallel (but we can ignore it)
Analysis
In order to demonstrate the insecurity of this proposal, we expose some its non-obvious features.
-
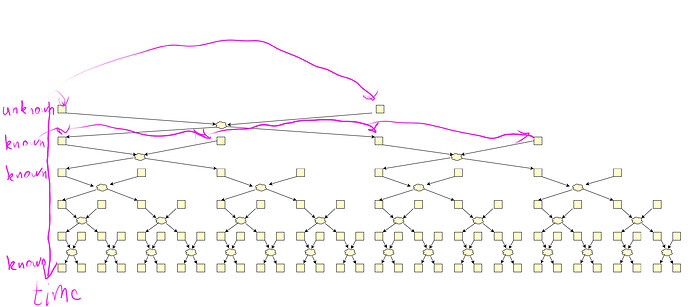
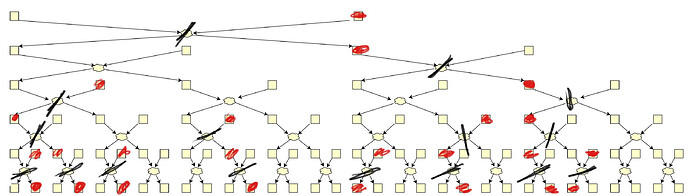
Only the first two commitments’ positions are unknown at the time of the swap. As next layers are stirred by next shufflers, the latter know the positions to be swapped.
-
Even though the first-touch commitment can end up in any of 32 positions, each output commitment origins from at most 6 input ones!
-
Every commitment owner can trace its own commitment and effectively destroy all swaps it undergoes.
-
Moreover, malicious owners can share their traces and kill many swaps.
-
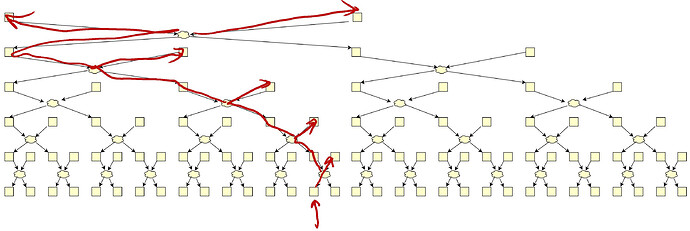
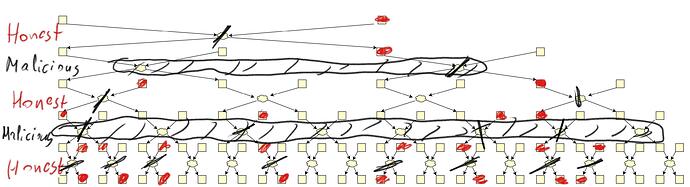
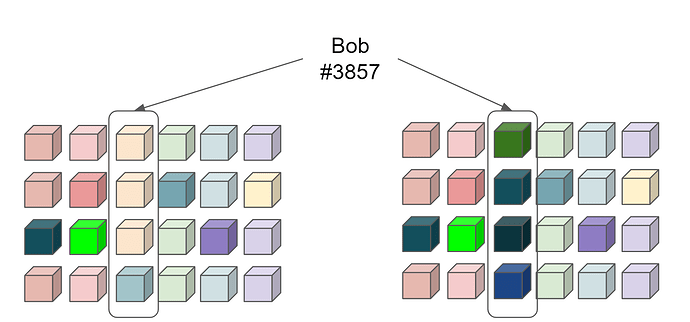
Malicious shufflers share their swaps and reduce the anonymity even further.
In this picture, only 10 swaps out of 31 survive, whereas we have <0.5 fraction of malicious.
- Malicious shufflers can even choose their swap to decrease the overall anonymity. Swapping right would destroy one more swap.
- In concrete numbers. For malicious fraction of \frac{1}{2} of shufflers&commitments with N=2^{14}:
- \frac{1}{2} of swaps are instantly killed
- \frac{1}{2} of honest commitments undergoing a tree are not secretly swapped.
- >5 commitments are fully known (no anonymity gain) after the full shuffle.
- Anonymity further degrades as honest proposers reveal themselves.
Summary
- Anonymity set for Swap-or-Not outputs is too small.
- Malicious shufflers reduce it a lot.
- We need way more iterations of it to get security compared to Whisk.
The attack does not work on Whisk
Whisk is an SSLE method, where N=2^{14} commitments are shuffled by M=2^{13} shufflers. Each shuffler makes his own stir of K=128 commitments
and provides a zero-knowledge proof of correctness. Whisk tolerates up to 1/2 corrupted or offline shufflers.
The attack does not apply to Whisk because the Whisk shuffles are much bigger (128 by default) and remain privacy-preserving even if a large fraction of the commitments is corrupt.