EDIT (01/08/2023): Remove any mention of permutation commitments (we don’t need them)
EDIT (01/08/2023): Replace Feistelshuffle with the simplified shuffling strategy
Hello all,
we are happy to present you Whisk: a block proposer election protocol tailored to the Ethereum beacon chain that protects the privacy of proposers.
Whisk is a modified version of the SSLE from DDH and shuffles scheme from the paper “Single Secret Leader Election” by Boneh et al. and is based on mixnet-like shuffling.
Along with the proposal, we also provide a feature-complete draft implementation of Whisk in the consensus-specs format, in an attempt to demonstrate and better reason about the overall complexity of the project. We link to the code throughout the proposal so that the reader gets a better understanding of how the system works.
Please treat this proposal as a draft that will be revised based on community feedback.
-
We are particularly interested in feedback about how Whisk compares to VRF-based solutions (like SASSAFRAS) and specifically how hard it would be to fit SASSAFRAS’ networking model into our networking model.
-
We are also interested in feedback about active RANDAO attacks against Whisk, and potential protocol variations that could improve the trade-offs involved.
It’s a read, so we invite you to brew some hot coffee, put on some tunes, recline and enjoy the proposal and the code!
Cheers!
PS: We also put the proposal on a hackmd in case people want to add inline comments (also ethresearch did not allow me to post the entire proposal, so the appendix will be in a separate comment).
Whisk: A practical shuffle-based SSLE protocol for Ethereum
Introduction
We propose and specify Whisk, a privacy-preserving protocol for electing block proposers on the Ethereum beacon chain.
Motivation
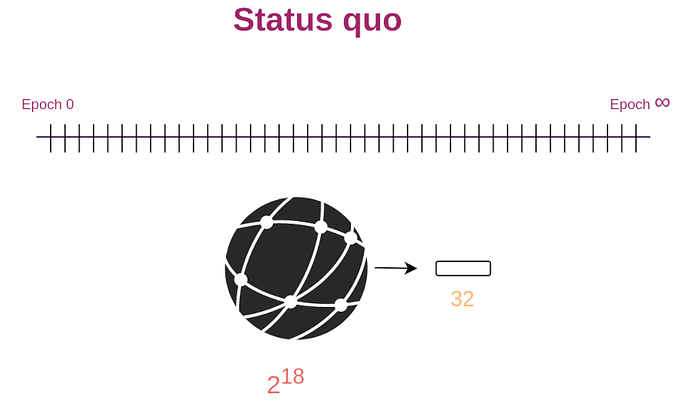
The beacon chain currently elects the next 32 block proposers at the beginning of each epoch. The results of this election are public and everyone gets to learn the identity of those future block proposers.
This information leak enables attackers to launch DoS attacks against each proposer sequentially in an attempt to disable Ethereum.
Overview
This proposal attempts to plug the information leak that occurs during the block proposer election.
We suggest using a secret election protocol for electing block proposers. We want the election protocol to produce a single winner per slot and for the election results to be secret until winners announce themselves. Such a protocol is called a Single Secret Leader Election (SSLE) protocol.
Our SSLE protocol, Whisk, is a modified version of the SSLE from DDH and shuffles scheme from the paper “Single Secret Leader Election” by Boneh et al.. Our zero-knowledge proving system is an adaptation of the Bayer-Groth shuffle argument.
This proposal is joint work with Justin Drake, Dankrad Feist, Gottfried Herold, Dmitry Khovratovich, Mary Maller and Mark Simkin.
High-level protocol overview
Let’s start with a ten thousand feet view of the protocol.
The beacon chain first randomly picks a set of election candidates. Then and for an entire day, block proposers continuously shuffle that candidate list thousands of times. After the shuffling is finished, we use the final order of the candidate list to determine the future block proposers for the following day. Due to all that shuffling, only the candidates themselves know which position they have in the final shuffled set.
For the shuffling process to work, we don’t actually shuffle the validators themselves, but cryptographic randomizable commitments that correspond to them. Election winners can open their commitments to prove that they won the elections.
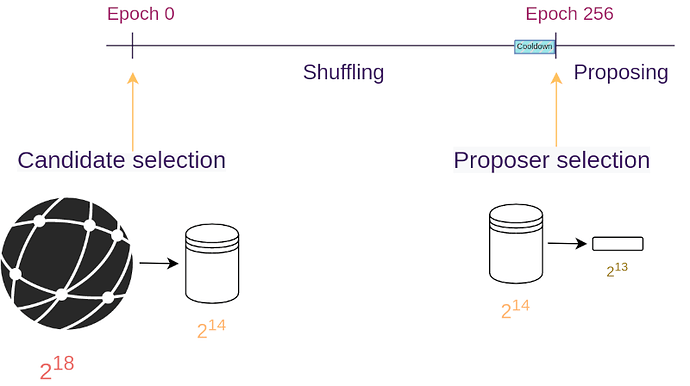
To achieve its goals, the protocol is split into events and phases as demonstrated by the figure below. We will give a high-level summary of each one in this section, and then dive into more details on the following sections:
- Bootstrapping event – where the beacon chain forks and the protocol gets introduced
- Candidate selection event – where we select a set of candidates from the entire set of validators
- Shuffling phase – where the set of candidates gets shuffled and re-randomized
- Cooldown phase – where we wait for RANDAO, our randomness beacon, to collect enough entropy so that its output is unpredictable
- Proposer selection event – where from the set of shuffled candidates we select the proposers for the next day
- Block proposal phase – where the winners of the election propose new blocks
Document overview
In the following section we will be diving into Whisk; specifying in detail the cryptography involved as well as the protocol that the validators and the beacon chain need to follow.
After that, we will perform a security analysis of Whisk, in an attempt to understand how it copes against certain types of attacks.
Following that we will calculate the overhead that Whisk imposes on Ethereum in terms of block and state size, as well as computational overhead.
We will then move into an analysis of alternative approaches to solve the problem of validator privacy and compare their trade-offs to Whisk.
We close this proposal with a discussion section which touches upon potential simplifications and optimizations that could be done to Whisk.
Protocol
In this section, we go through the protocol in detail.
We start by introducing the cryptographic commitment scheme used. We proceed with specifying the candidate and proposer selection events, and then we do a deep dive into the shuffling algorithm used.
We have written a feature-complete draft consensus implementation of Whisk. Throughout this section, we link to specific parts of the code where applicable to better guide readers through the protocol.
Commitment scheme
For the shuffling to work, we need a commitment scheme that can be randomized by third parties such that the new version is unlinkable to any previous version, yet its owner can still track the re-randomized commitment as her own. Ideally, we should also be able to open commitments in a zero-knowledge fashion so that the same commitment can be opened multiple times. We also need Alice’s commitment to be bound to her identity, so that only she can open her commitment.
We use the commitment scheme suggested by the SSLE paper where Alice commits to a random long-term secret k using a tuple (rG, krG) (called a tracker in this proposal). Bob can randomize Alice’s tracker with a random secret z by multiplying both elements of the tuple: (zrG, zkrG). Finally, Alice can prove ownership of her randomized tracker (i.e. open it) by providing a proof of knowledge of a discrete log (DLOG NIZK) that proves knowledge of a k such that k(zrG) == zkrG.
Finally, we achieve identity binding by having Alice provide a deterministic commitment com(k) = kG when she registers her tracker. We store com(k) in Alice’s validator record, and use it to check that no two validators have used the same k. We also use it at registration and when opening the trackers to check that both the tracker and com(k) use the same k using a discrete log equivalence proof (DLEQ NIZK). Fr more details see the “Selling attacks” section of this document and the duplication attack section in the SSLE paper.
Protocol flow
Now let’s dive deeper into Whisk to understand how candidates are selected and how proposing works. For this section, we will assume that all validators have registered trackers. We will tackle registration later in this document.
The protocol starts with the beacon chain using public randomness from RANDAO to sample 16,384 random trackers from the entire set of validators (currently around 250,000 validators). The beacon chain places those trackers into a candidate list.
After that and for an entire day (8,192 slots), block proposers shuffle and randomize the candidate list using private randomness. They also submit a zero-knowledge proof that the shuffling and randomization were performed honestly. During this shuffling phase, each shuffle only touches 128 trackers at a time; a limitation incurred by the ZKP performance and the bandwidth overhead of communicating the newly-shuffled list of trackers. The strategy used for shuffling will be detailed in the next section.
After the shuffling phase is done, we use RANDAO to populate our proposer list; that is, to select an ordered list of the 8,192 winning trackers that represent the proposers of the next 8,192 slots (approximately a day). We stop shuffling one epoch before the proposer selection occurs, so that malicious shufflers can’t shuffle based on the future result of the RANDAO (we call this epoch the cooldown phase).
Finally, for the entire next day (8,192 slots), we sequentially map the trackers on the proposer list to beacon chain slots. When Alice sees that her tracker corresponds to the current slot, she can open her tracker using a DLEQ NIZK and submit a valid block proposal.
This means that the proposal phase lasts for 8,192 slots and the same goes for the shuffling phase. This creates a day-long pipeline of Whisk runs, such that when the proposal phase ends, the shuffling phase has also finished and has prepared the 8,192 proposers for the next day.
Shuffling phase
In the previous section, we glossed over the strategy used by validators to shuffle the candidate list (of size 16,384) with small shuffles (of size 128). Shuffling a big list using small shuffles (called stirs from now on) requires a specialized algorithm, especially when a big portion of shufflers might be malicious or offline. We call our proposed algorithm Randshuffle.
Randshuffle
At every slot of the shuffling phase, the corresponding proposer picks 128 random indices out of the candidate list. The proposer stirs the trackers corresponding to those indices by permuting and randomizing them.
See the Distributed Shuffling in Adversarial Environments paper for the security analysis of the Randshuffle algorithm.
Proofs of correct shuffle
Validators must use zero-knowledge proofs to show that they have shuffled honestly: that is, to prove that the shuffle output was a permutation of the input and that the input trackers actually got randomized. If no such proofs were used, a malicious shuffler could replace all trackers with her own trackers or with garbage trackers.
We will now take a look at the zero-knowledge proofs used by Whisk.
Verifiable shuffling has been a research topic for decades due to its application in mixnets and hence to online anonymity and digital election schemes. Already since twenty years ago, zero-knowledge proofs based on randomizable ElGamal ciphertexts have been proposed, and in recent years we’ve seen proofs based on CRS and pairings as well as post-quantum proofs based on lattices.
In Whisk we use shuffling ZKPs that solely rely on the discrete logarithm assumption and don’t require a trusted setup while still maintaining decent proving and verification performance. Our proofs are heavily based on previous work on shuffling arguments by Bayer and Groth and they also incorporate more recent optimizations inspired by the inner product arguments of Bulletproofs.
We have implemented an initial PoC of the shuffling proofs and we are working on a more robust implementation that includes test vectors and can be used as a solid basis for writing production-ready code for Ethereum clients.
Bootstrapping
In all previous sections, we’ve been assuming that the system has bootstrapped and that all validators have Whisk trackers and commitments associated with them. In this section, we show how to do bootstrapping.
We bootstrap Whisk by having the beacon chain initialize all validators with dummy predictable commitments. We then allow validators to register a secure commitment when they propose a new block.
This means that the system starts in an insecure state where the adversary can predict future proposers (similar to the status quo), and as more validators register secure commitments, the system gradually reaches a secure steady state.
Security analysis
In this section, we analyze Whisk’s security and privacy.
We first see how Whisk effectively expands the anonymity set of proposers. We then explore various active attacks that could be performed against Whisk: either by malicious shufflers or by the Ethereum randomness beacon (RANDAO). We close this section by demonstrating how Whisk is protected against selling attacks, where an adversary attempts to buy specific proposer slots.
Anonymity set
The core idea of Whisk is to significantly increase the anonymity set of block proposers. In particular, the anonymity set increases from the status quo of a single validator to at least 8,192 validators (which correspond to the number of candidates that did not get selected as proposers)
To make this concrete, the adversary knows the identities of the validators that got selected as candidates. However, because of the shuffling phase, she cannot tell which of those validators got selected as proposers at the end of the protocol. This means that the 8,192 candidates that were not selected as proposers become the anonymity set for all proposers.
It’s worth noting that those 8,192 validators actually correspond to a significantly smaller number of nodes on the P2P layer. For example, the current validator set of 250,000 validators is represented by about 5,000 P2P nodes. While it’s not known how validators are distributed to this small number of nodes, for this analysis we can assume that the distribution follows something close to the Pareto principle where “20% of the nodes run 80% of the validators”. Doing a simulation with this distribution we find that an anonymity set of 8,192 validators corresponds to 2,108 nodes on average. That is explained by the fact that even though there are some “heavy nodes” that will always appear in the anonymity set and will control a hefty portion of it, there is also a long tail of “light nodes” that run one or two validators that helps increase the size of the anonymity set.
Whisk can also be adapted to produce a bigger anonymity set by increasing the size of the candidate list while keeping the size of the proposer list the same. However, doing such a change requires analyzing our shuffling strategy to see if it can sufficiently shuffle a bigger candidate list. Alternatively, we could increase the size of our stirs but we would need to be certain that this does not render our ZKPs prohibitively expensive.
Active attacks through RANDAO biasing
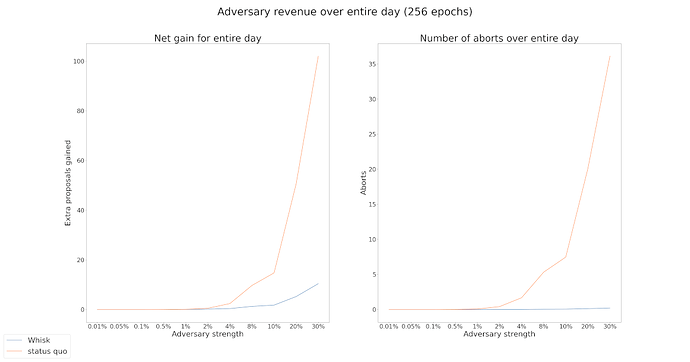
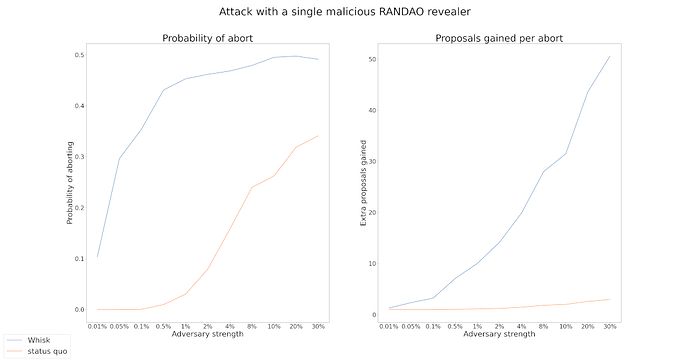
In this section, we analyze Whisk’s resilience against RANDAO biasing attacks. While we present the main results here, the detailed analysis can be found in the Appendix.
Whisk uses RANDAO in the candidate selection and proposer selection events. This opens it up to potential RANDAO biasing attacks by malicious proposers. Since RANDAO is a commit-and-reveal protocol it enables attackers who control the last k proposers before the candidate/proposer selection event to choose between 2^k possible candidate or proposer lists. This quickly becomes profitable for rational attackers, since they can increase profit by abandoning the commit-and-reveal protocol and choosing the list that contains the maximal number of validators they control or that gives them control over specific proposer slots.
Similar attacks can also be performed on the current Ethereum proposer selection where we publicly sample 32 proposers at the beginning of each epoch using RANDAO (see figure below).
By comparing Whisk with the status quo, we found that while big adversaries can extract bigger profits in the status quo, Whisk allows even small adversaries to extract profits by attacking RANDAO once per day. Please see the Appendix for more details on the results.
One way to completely address such RANDAO attacks is to use an unbiasable VDF-based randomness beacon. However, until a VDF beacon gets deployed, such attacks pose a risk both against the status quo and the Whisk protocol.
One possible variation is to make the security of Whisk identical to the security of the status quo with regards to RANDAO attacks by spreading candidate selection and proposer selection over an entire day (as seen in the figure below) instead of doing them on a single moment in time. However, even the status quo security is not ideal, and by implementing this defense we complicate the protocol further.

Selling attacks
We want to prevent Mallory from being able to buy and open Alice’s k.
It’s important to prevent that since that would allow Mallory to buy proposer slots on the beacon chain from an automated auction smart contract, or it could also create a situation where a single k is opened by two validators causing problems with the fork choice.
The commitment scheme presented above prevents that by doing a uniqueness check against k using com(k), and also by saving com(k) in Alice’s validator record and making sure that whoever opens using k also has com(k) in their validator record.
Let’s walk through a potential selling scenario and see how the identity binding prevents it:
- Alice registers (rG, krG), com(k)
- Mallory registers (rG, prG), com(p) (she can’t register with k because of the uniqueness check)
- …
- During the proposal phase, (rG, krG) becomes the winning tracker
- Mallory attempts to propose using k by sending a DLEQ NIZK that proves that k is both the dlog of k(rG) and also the dlog of com(k)=kG
In this case the beacon chain would dig into Mallory’s validator record and use com(p) as the instance when verifying the NIZK. At that point, the verification would fail and Mallory’s proposal would be discarded.
Overhead analysis
In this section, we calculate Whisk’s overhead in terms of block and state size, as well as the computational overhead imposed on validators.
State size overhead
The overhead of Whisk on the BeaconState is 45.5MB for 300k validators. In detail:
- a candidate list (16,384 trackers) (16,384*96 = 1.57 MB)
- a proposer list (8,192 trackers) (8,192*96 = 0.78 MB)
- a tracker for each validator (96 bytes per validator) (28.8 MB for 300k validators)
- a com(k) for each validator (48 bytes per validator) (14.4 MB for 300k validators)
In more detail, each validator is currently adding 139 bytes to the state, but with Whisk it will add 283 bytes.
This represents a dramatic increase in the size of the BeaconState (currently sitting at 30MB).
It’s worth noting that the tracker and com(k) of each validator (43.2MB for 300k validators) never change once they get registered which allows implementations to save space by keeping a reference of them in memory that can be used across multiple state objects.
For various ideas on how to reduce the state size, see the discussion section.
Block size overhead
The overhead of Whisk on the BeaconBlockBody is 16.5 kilobytes. In detail:
- a list of shuffled trackers (128 trackers) (128*96 = 12,288 bytes)
- the shuffle proof (atm approx 82 G1 points, 7 Fr scalars) (4,272 bytes)
- one fresh tracker (two BLS G1 points) (48*2 = 96 bytes)
- one com(k) (one BLS G1 point) (48 bytes)
- a registration DLEQ proof (two G1 points, two Fr scalars) (48*4 = 192 bytes)
The overhead of Whisk on the BeaconBlock is 192 bytes. In detail:
- an opening DLEQ proof (two G1 points, two Fr scalars) (48*4 = 192 bytes)
Computational overhead
The main computationally heavy part of this protocol is proving and verifying the zero-knowledge proofs involved.
We wrote a PoC of the ZKPs using an old version of arkworks-rs (zexe) and the BLS12-381 curve and found that in an average laptop:
- Shuffling and proving the shuffle takes about 880ms (done by block proposers)
- Verifying the proof takes about 21ms (done by validators)
Our benchmarks were a PoC and we believe that a production-ready implementation of the shuffling/verifying procedure can provide a 4x-10x boost on performance by:
- Moving from zexe to the latest arkworks-rs or a more optimized library (e.g. blst)
- Moving from BLS12-381 to a curve with faster scalar multiplications
- Further optimizing the proofs and their implementation
If the proving overhead is considered too high, we can alter the shuffling logic so that validators have time to precompute their proofs in advance. For example, we can avoid shuffling on the last slot before each new round of the shuffling algorithm. At that point, the shuffling matrix for the next round is fully determined and hence validators have at least 12 seconds to shuffle and precompute their proofs for the next round.
Related work
There are more ways to solve the problem of validator privacy. Each approach comes with its trade-offs and each use case should pick the most suitable approach. In this section, we go over different approaches and discuss their trade-offs.
SASSAFRAS
The Polkadot team has designed an SSLE protocol called SASSAFRAS which works using a combination of a ring-VRF and a network anonymity system.
The scheme works by having each validator publish a VRF output (i.e. election ticket) through a native single-hop anonymity system. After some time, the chain sorts all received tickets to create the future proposer ordering, and when it’s Alice’s time to claim a slot, she submits a proof that it was actually her ticket that won this round.
SASSAFRAS turns their VRF scheme into a ring-VRF through the use of SNARKs ensuring this way that the VRF output was generated from a specific set of public keys and no duplicate or garbage tickets were submitted.
Benefits
A significant benefit of SASSAFRAS over Whisk is that it doesn’t require any shuffling which reduces the consensus complexity of the system. This means that state manipulation is minimal in SASSAFRAS, while in Whisk we are fiddling with the state at every slot. For the same reason, the state space required is significantly less, since the chain mainly needs to hold the VRF output of each validator (plus a pubkey), whereas in Whisk we are storing multiple commitments per validator plus the entire shuffling list. Finally and perhaps most importantly, the consensus simplicity of SASSAFRAS makes it more flexible when it comes to supporting other features (e.g. elect multiple leaders per slot or doing gradual RANDAO samplings).
A further benefit of SASSAFRAS is that the anonymity set of each proposer spans the entire validator set, in contrast to Whisk where the worst-case anonymity set is 8,192 validators.
Drawbacks
The main drawback of SASSAFRAS is that instead of shuffling, it uses a network anonymity layer to detach the identity of the validator from her ticket.
For this purpose, SASSAFRAS builds a simple single-hop timed mixnet inside its p2p layer: When Alice needs to publish her ticket, she does ticket (mod len(state.validators)) and that gives her Bob’s validator index. She uses Bob as her proxy and sends her ticket to him. Then Bob uploads it on-chain by sending a transaction with it. Effectively, Bob acted as the identity guard of Alice.
An issue here is that network anonymity comes with a rich literature of attacks that can be applied in adversarial environments like blockchains. At the most basic level, in the above example, Bob can connect the identity of Alice with her published ticket. Effectively this means that a 10% adversary can deanonymize 10% of tickets.
At a more advanced level, an eavesdropper of a validator’s network can launch traffic correlation attacks in an attempt to correlate the timing of received tickets with the timing of outbound tickets. Traffic correlation attacks effectively reduce the anonymity set of the system. The classic solution is for protocol participants to send fake padding messages; however designing such padding schemes requires careful consideration to not be distinguishable from real traffic.
Another interesting aspect of SASSAFRAS is that it assumes a mapping between validators and their P2P nodes. Creating and maintaining such a mapping can be done with a DHT protocol but it complicates the networking logic especially when a validator can correspond to multiple dynamic nodes. Fortunately, validators can still fallback to sending their ticket in the clear if such a system experiences a transient break.
Also, if the unique proxy validator of a ticket is faulty or offline, the validator is forced to publish the ticket themselves, effectively getting deanonymized.
With regards to cryptography, the current PoC implementation of the ring-VRF uses Groth16 SNARKs which require a trusted setup. However, the SNARKs could potentially be rewritten to use Halo2 or Nova which don’t require a ceremony.
Finally, not all parts of SASSAFRAS have been fully specified (e.g. the bootstrapping logic), which might produce some yet unseen complexity.
All in all, SASSAFRAS is an SSLE protocol with higher networking complexity but lower consensus complexity. It’s important to weigh the trade-offs involved especially with regards to Ethereum’s networking model and overall threat model.
Other networking-level defenses
In this proposal we’ve been assuming that it’s trivial for attackers to learn the IP address of every beacon chain validator.
Dandelion and Dandelion++ are privacy-preserving networking protocols designed for blockchains. They make it hard for malicious supernodes on the p2p network to track the origins of a message by propagating messages in two phases: a “stem” anonymity phase, and a spreading “fluff” phase. During the “stem” phase each message is passed to a single randomly-chosen node, making it hard to backtrack it.
Systems similar to Dandelion share networking complexities similar to the ones mentioned above for SASSAFRAS. Furthermore, using Dandelion for block proposal needs careful consideration of latency so that it fits inside the four seconds slot model of Ethereum (see Figure 11 of Dandelion++ paper)
An even simpler networking-level defense would be to allow validator nodes to use different network interfaces for attestations and block proposals. This way, validators could use one VPN (or Tor) for attestations and a different one for proposals. The problem with this is that it increases setup complexity for validators and it also increases the centralization of the beacon chain.
Drawbacks of Whisk
It’s worth discussing the drawbacks of Whisk especially as we go through the process of comparing it against other potential solutions (e.g. VRF-based schemes).
First and foremost, Whisk introduces non-negligible complexity to our consensus protocol. This makes the protocol harder to comprehend and analyze, and it also makes it harder to potentially extend and improve.
For example, because of the lengthy shuffling phase it’s not trivial to tweak the protocol to elect multiple leaders per slot (which could be useful in a sharded/PBS/crList world). That’s because we would need bigger candidate and proposer lists, and hence a bigger shuffling phase. While it’s indeed possible to tweak Whisk in such a way, it would probably be easier to do so in a VRF-based scheme.
Whisk also slightly increases the computational overhead of validators who now need to create and verify ZKPs when creating and verifying blocks. It also increases the computational overhead of P2P nodes, since they now need to do a DLEQ verification (four scalar multiplications) before gossiping.
Finally, a drawback of SSLE in general (not just of Whisk) is that it completely blocks certain protocol designs. For example, it becomes impossible to ever penalize validators who missed their proposal. SSLE also prevents any designs that require the proposer to announce themselves before proposing (e.g. to broadcast a crList).
Discussion
Simplifications and Optimizations
In this section, we quickly mention various simplifications and optimizations that can be done on Whisk and the reason we did not adopt them:
-
Moving the commitment scheme from BLS12-381 to a curve with a smaller base field size (but still 128 bits of security) would allow us to save significant state space. For a 256-bit curve, group elements would be 32 bytes which is a 33% improvement over the state space (BLS12-381 G1 elements are 48 bytes). We used BLS12-381 in this proposal because the consensus specs are already familiar with BLS12-381 types and it’s unclear how much work it would be to incorporate a different curve in consensus clients (e.g. curve25519 or JubJub).
-
We can store H(kG) in the state instead of com(k) to shave 12 bytes per validator. But then we would need to provide kG when we propose a block and match it against H(kG) which slightly complicates the protocol.
-
Instead of using com(k) to do identity binding on k, we could do identity binding by forcing the hash prefix of H(kG) to match Alice’s validator index. Alice would brute force k until she finds the right one. This would save space on the state, but it would make it hard to bootstrap the system (we would need to use a lookup table of
{validator_index -> k}) -
Instead of registering (rG, krG) trackers, we could just register with kG (i.e. not use a randomized base) to simplify the protocol and save space on the block and on the state. However, this would make it easier for adversaries to track trackers as they move through shuffling gates by seeing if they have the same base, which becomes a problem if the set of honest shufflers is small.
-
We could do identity binding by setting k = H(nonce + pubkey) as the SSLE paper suggests which would simplify the protocol. However, we would need to completely reveal k when opening which causes problems if the same validator gets selected as a candidate twice (either in the same run or in adjacent runs) since now adversaries can track the tracker around.