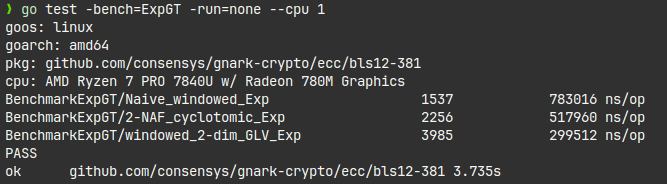
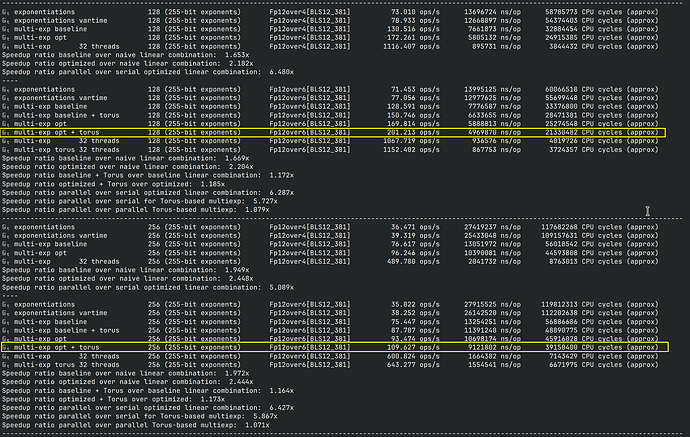
The return of Torus Based Cryptography: Whisk and Curdleproof in the target group
In the last two years the Ethereum Foundation has been working hard to devise a practical shuffle-based Single Secret Leader Election (SSLE) protocol. This dedicated effort by the Ethereum Foundation’s research team has culminated in the creation of two remarkable protocols: Whisk and Curdleproof (a zero-knowledge shuffle argument inspired by BG12).
A series of posts by Dapplion:
- Whisk: Induced missed initial slots
- Whisk: Expensive duty discovery
- Whisk: the bootstrapping problem
accurately describes the status quo.
The problem that we are discussing and trying to solve in this post is the bootstrapping problem. To gain a clearer insight into this challenge, let’s take a moment to revisit the workings of Whisk.
For the rest of this post:
- G_1, G_2 are the BLS12-381 generators
- g_T = e(G_1,G_2)
Whisk’s recap
As mentioned above Whisk is a proposal to fully implement SSLE from DDHand shuffles scheme (see also section 6 from Boneh et al paper).
The idea behind this solution is pretty straightforward and neat. Let’s list below the key ingredients of the commitment scheme in Whisk (at the net of the shuffles):
- Alice commits to a random long-term secret k using a tuple (rG,krG) (called tracker).
- Bob randomizes Alice’s tracker with a random secret z by multiplying both elements of the tuple: (zrG,zkrG).
- Alice proves ownership of her randomized tracker (i.e. open it) by providing a proof of knowledge of a discrete log (
DLOG NIZK) that proves knowledge of a k such that k(zrG)==zkrG . - Identity binding is achieved by having Alice provide a deterministic commitment com(k)=kG when she registers her tracker.
- We also use it at registration and when opening the trackers to check that both the tracker and com(k) use the same k using a discrete log equivalence proof (
DLEQ NIZK).
Whisk can be implemented in any group where the Decisional Diffie Hellman problem (DDH) is hard. Currently Whisk is instantiated via a commitment scheme in BLS12-381.
So far, everything is going well. BUT, the question remains: which long-term secret ‘k’ should be used?
Bootstrapping problem and de-anonymization
This problem is discussed at length in Dapplion’s post, but just to give you a flavor of the issue, let’s assume we take the easy way and use the validator’s secret signing key k and its associated public key kG_1 for bootstrapping. The issue here is that if the validator signs at least one message where the message M is known (this is usually true for attestation), the validator’s tracker could be de-anonimized forever with a single pairing operation:
e(rG_1, kH(m)) \stackrel{?}{=} e(rk G_1, H(m))
So it is clear that the pairing operation is acting as a de-anonymization oracle.
Using the target group
In order to contrast the pairing oracle, Justin Ðrake proposed instantiating Whisk using the target group instead.
Note: As it is customary, we will switch to multiplicative notation.
Naive Whisk implementation using the target group
- Alice commits to a random long-term secret k using a tuple (g_T^r,g_T^{kr}) (called tracker).
- Bob randomizes Alice’s tracker with a random secret z by exponentiating both elements of the tuple: (g_T^{zr},g_T^{zkr}).
- Alice proves ownership of her randomized tracker (i.e. open it) by providing a proof of knowledge of a discrete log (
DLOG NIZK) that proves knowledge of aksuch that (g_T^{zr})^k==g_T^{zkr} . - Identity binding is achieved by having Alice provide a deterministic commitment com(k)=g_T^k when she registers her tracker.
- We also use it at registration and when opening the trackers to check that both the tracker and com(k) use the same k using a discrete log equivalence proof (
DLEQ NIZK).
N.B.: In case there are concerns about exposing the validator key k, please note that g_T^{kr} is nothing else that e(rG_1.kG_2).
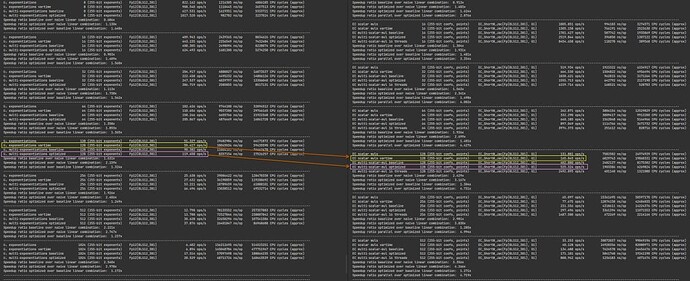
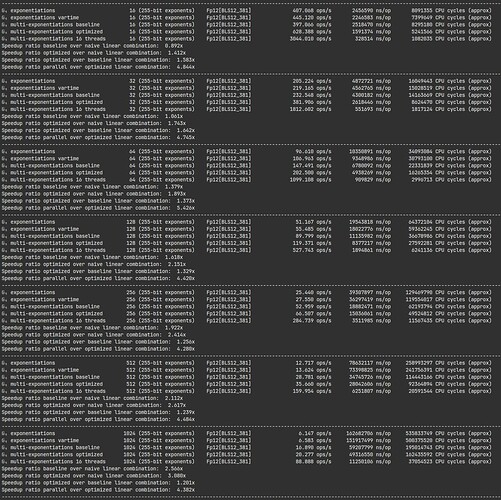
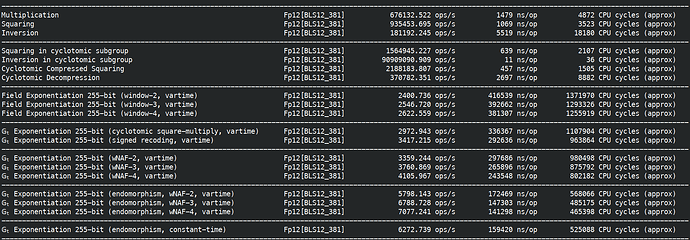
The downsize of this approach respect to the current status quo is that the coordinates of g_T lie in a large finite field \mathbb{F}^*_{p^{12}} in this case. This makes the scheme a considerably slower.
In the next section we show an attempt to improve the situation a bit.
XTR and CEILIDH to the rescue
XTR is a Public Key System that was designed by A. Lenstra and E. Verheul presented at CRYPTO 2000. XTR stands for Compact Subgroup Trace Representation and it is based on a clever observation that elements in G_{p^2-p+1}, where a prime order N subgroup G_N \subset G_{p^2-p+1} with N dividing \Phi_6(p)=p^2-p+1, can be compactly represented by their trace over \mathbb{F}^*_{p^2} which is defined by:
Tr: x \rightarrow x + x^{p^2}+x^{p^4}
Lenstra and Verheul showed that if g \in G_{p^2-p+1} and c = Tr(g) then it is possible to work eficiently and compactly using the compressed generator (with some limitations that we explore in the next subsection).
Here you can find an example of the DH protocol implented applying XTR to the target group of the BLS6 curve defined in this paper.
The XTR cryptosystem works well in the cyclotomic subgroup of \mathbb{F}^*_{p^6} for prime p, although it is possible to generalize it to extension fields \mathbb{F}^*_{q^6} with q = p^m making it compatible with the target group of BLS12-381.
Limitations of XTR
One drawback of using traces, as XTR does, is that the compression is not lossless, which can lead to the mapping of conjugates into identical compressed elements. However, this is not a significant issue since it is possible to employ a trace-plus-a-trit method to compress and decompress elements, much like what is done for elliptic curve compressed points.
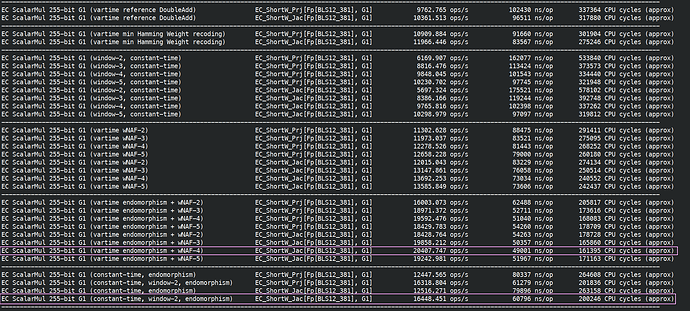
Another, more stringent issue to consider is this: performing a single exponentiation (Tr(g^x)) in compressed form is easy, and a double exponentiation (Tr(g^xh^y)) is feasible. However, going beyond that and performing more complex operations in a compressed format is not really feasible (this limitation resembles what we encountered when attempting to translate the SSLE protocol into the isogeny/action group setting). Consequently, the XTR setting may not be suitable for porting all discrete-log cryptosystems. We believe that translating Whisk into the XTR setting is a simple exercise, while more caution needs to be applied to Curdleproof.
CEILIDH
A significantly cleaner approach to lossless compression can be found in algebraic tori, as introduced by Rubin and Silverberg in 2003. They presented two novel systems: \mathbb{T}_2, designed as a substitute for LUC and utilizing quadratic extension fields, and CEILIDH, positioned as an alternative to XTR. CEILIDH, pronounced as “Cayley,” was introduced as an acronym representing “Compact, Efficient, Enhancements over LUC, Enhancements over Diffie–Hellman” and is primarily a factor-3 compression and decompression technique designed for “hard” subgroups of sextic extension fields, lacking an efficient exponentiation method. However, it is possible to enhance CEILIDH by combining it with efficient arithmetic over compressed element.
Conclusion
In an attempt to address the bootstrapping problem in Whisk, we explored the potential of using the target group and discussed the application of XTR and CEILIDH. While XTR does exhibit some limitations, both XTR and CEILIDH present a promising path for achieving lossless compression and improved efficiency in discrete-log cryptosystems. To the best of our knowledge, this may be the first deployment of a real-life protocol employing XTR. We will dedicate time to investigate further and will report back on our findings. For an in-depth overview of XTR and Tori, refer to the excellent paper by Martijn Stam.
Acknowledgments: We would like to thank Justin Drake, Robert Granger, Ignacio Hagopian, Gottfried Herold, Youssef El Housni, George Kadianakis, Mark Simkin, Dapplion, Michael Scott for fruitful discussions.