Single and non-single proposer selection: introduction and context
Ethereum’s current approach to proof of stake works by picking a single validator using a publicly computable random function to be the proposer for each slot. This is in contrast to PoW, where instead every validator has an independent random chance of being a valid proposer at any given time.
Ethereum’s single-proposer approach always picks exactly one proposer, whereas the PoW-style approach gives a Poisson distribution, and so often selects multiple proposers at the same time (in which case, the proposer with the better internet connection gets an unfair advantage). However, the single-proposer approach makes the proposer publicly known ahead of time, making them vulnerable to DoS attacks.
Single secret leader election (see: Whisk) aims to get the best of both worlds: select a single proposer using a cryptographic procedure that ensures that only the proposer knows when they are selected. Each validator submits a commitment to a secret, and then the commitments are repeatedly blinded and re-shuffled. When it comes time to choose a proposer, a random commitment is publicly chosen, but because of the blinding only the proposer knows that the commitment corresponds to them.
This post explores an alternative based on protocol engineering rather than cryptography: what if we remove the requirement to have a single chosen leader? What if we go back to giving each validator an independent random chance of being a valid proposer, but actually try to handle conflicts fairly?
A concrete proposal
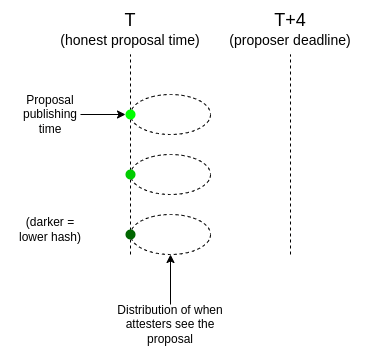
Suppose that there are N active validators. Each validator has a \frac{5}{N} chance of being a valid proposer at any given slot. One simple way of implementing this is to require that the hash of the randao reveal of the block must be less than \frac{2^{256} * 5}{N}. The randao reveal has the property that there is only one possible valid value that any validator can generate in any slot, but this value can only be calculated ahead of time by the validator themselves. This is ideal: it means that only the validator themselves can know ahead of time whether or not they are a valid proposer at a given slot.
The above parameters create a Poisson distribution with \lambda=5. During each slot, there is a 1 - e^{-5} \approx 99.3\% chance of having at least one proposer. However, there is also a \approx 96\% chance that there will be more than one proposer. How could we fairly, and safely, deal with this situation?
Fairness alone is easy to solve: if there are multiple proposers, they all propose, and the one with the lowest randao reveal hash wins. But is this safe?
Easy case: all valid proposers honest or offline
All proposers propose at time T, and all proposals reach all attesters before T + 4. Attesters all vote for the proposer with the lowest randao reveal, and so there is one leading proposer with a large fork choice advantage over the others.
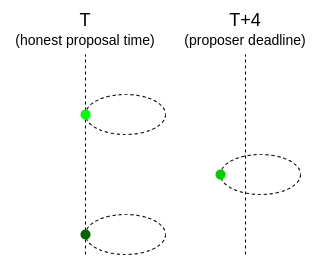
Medium case: the lowest-hash proposer is honest, some other proposers are dishonest
The lowest-hash proposer proposes at time T, and their proposal reaches all attesters before T + 4. Some attesters see other proposals as well, others don’t. However, they still all vote for the same lowest-hash proposer, and so there is one leading proposer with a large fork choice advantage over the others.
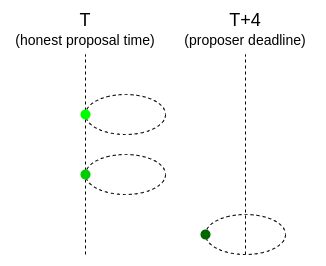
Hard case: the lowest-hash proposer is dishonest
The lowest-hash proposer P_1 proposes at time T+3.5; some attesters see it before T+4 and others do not. The network is split between attesters voting for P_1 and attesters voting for some other P_2 (or occasionally an empty slot).
This is the same situation as what happens in the status quo, and so far we’ve established that it happens with only the same probability as in the status quo (and not a higher probability because of multiple proposers). The question, however, is: is recovery harder?
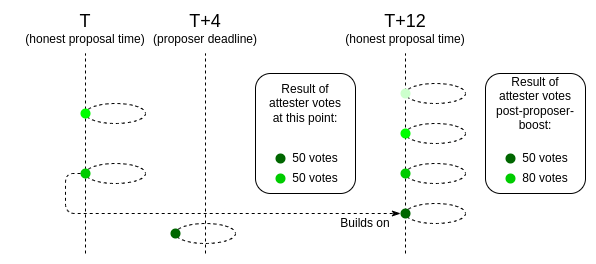
Recovery in the status quo happens through proposer boosting. We assume that the chain continues to be potentially chaotic for one or more slots until there is a slot with an honest proposer. At that point, the honest proposer produces a block, and we give that block an extra bonus to their fork choice score, enough to override a large portion of the attesters. The attesters for that next slot, when computing the fork choice, only take into account attestations that they received before the start of that slot, plus the proposer boost, and so there is one single actor that “pushes” the fork choice split to one side or the other.
Can we replicate proposer boosting in the multi-proposer case? It seems that we can: we only apply the proposer boost to the lowest-hash proposal. The attestations are published at time T+4, which is also the attesters’ deadline for receiving proposals. Hence, they know about all of the proposals that they will consider, and so they can figure out which one has the lowest hash and apply the proposer boost to it. If the lowest-hash proposer is honest, this will work for the same reasons why proposer boosting works in the status quo.
The main difference is that if the lowest-hash proposer is malicious, then attesters may have a 2x larger disagreement in their fork choice views: instead of some attesters seeing the boost and others seeing no boost, some see a boost in one direction and others see a boost in the other direction. This may reduce the maximum safe size of a boost by up to 2x and should be studied more, but is not a fatal flaw.
Extending to PBS
One small change to the current PBS proposal seems to be required. In the current proposal, the proposer boost of a builder is larger than the entire attestation committee. This would be risky in a multiple-proposer-per-slot world for a similar reason to what is identified above: if a builder builds on a block B_1, but there is a proposer with a lower-hash randao that has not yet published, then they could release B_2 and steal the MEV from B_1. The fix is to make the builder’s proposer boost smaller, so that the builder B_1 would only publish after attestations on top of B_1 have been made and those attestations would ensure that it beats B_2 in the fork choice and B_2's proposer boost would not overrule them.