TLDR: This post offers a thought framework for analysis of the decentralisation efforts of new and existing rollups.
Overview
This post outlines a framework to analyse different design choices, and their downstream consequences, in the process of decentralising rollups. None of the design choices outlined below can be taken in isolation and any of the design choices can effectively, disable a whole set of other choices. Therefore it does not aim to set a priority of choice in isolation to any single design option. The design choices are picked with ZK rollups in mind, but similar reasoning can be applied for Optimistic rollups.
This framework can be used for retroactive analysis of proposed decentralisation decisions made by rollup architects, or be used as the basis for designing novel rollup iterations optimised for certain tradeoffs.
The first part of this document offers short definition of the design areas that the architects need to make decisions in. It is by no means an exhaustive list of the design areas a rollup designer needs to consider, but highlights some major ones that influence most of the rollup decentralisation design.
The second part of this document offers the authors take on the spectrum of possible design options that a designer can make. Furthermore it offers analysis what tradeoffs the various ends of the spectrum offer.
The last part of this document offers examples on fictitious rollups aiming to showcase the usage and usefulness of this analysis framework.
Design Areas
Sequencer Choice
Design choice on how sequencers (one or multiple) become eligible for proposing new batches of sequences on the L1 (more accurately - the data availability layer
Prover Choice
Design choice on how provers coordinate generation and submission of proofs.
Explicit Sequencer-Prover Coupling
Should the sequencers be allowed to choose their provers or not.
Allowing Forks
The rollup has to chose if a certain previous sequenced state X can be used as basis for multiple competing sequences that produce post-sequence state X’.
Number of Forks Proven
The rollup has to chose if one or multiple (if applicable) forks should be proven at the same time.
Synchronous vs Asynchronous Proofs
If we consider the rollup as a chain of sequences each based on а (valid) previous sequence, a design decision must be made on whether sequences are proven synchronously (f.e. sequentially) or enable asynchronously (proving of sequences ahead of time).
Incentives
The crypto-economical incentives of the rollup are a major design component and influences hugely the tradeoffs that the rollup uses. Depending on the priority and assurance of payment for sequencers and provers, one can optimise for either transaction throughput, transaction cost and or finality time.
When designing the sequencers and provers incentives, the designer needs to consider the combinations between the two. A set of choices on the sequencer side, disables a set of choices on the prover side, and vice versa.
Sequencers Incentives
What are the incentives for the sequencers to provide high quality service.
Prover Incentives
What are the incentives for the provers to provide high quality service.
Design Choices
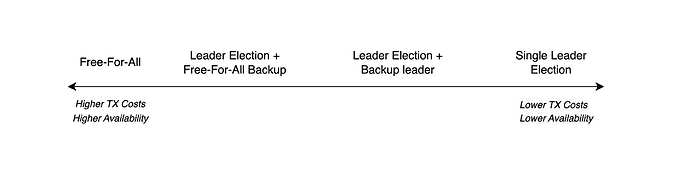
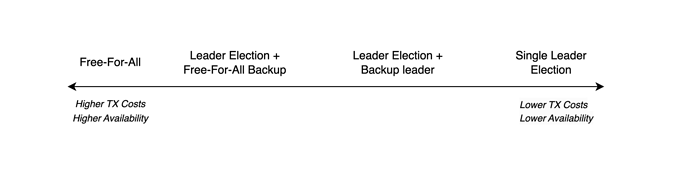
Sequencer Choice
“Leader Election” sees a single sequencer being elected and be known ahead of time (preferably known only by the leader himself). Various algorithms can be used - like PoS + RANDAO, SSLE (f.e. Whisk: A practical shuffle-based SSLE protocol for Ethereum), etc. If a single leader election is chosen, the main follow up topics of the design that need to be considered have to do with accounting for liveness of the leader.
“Free for All” sees no single leader being elected and all actors can include sequences. If Free for All is chosen, the main consideration is capital efficiency - cost of the system (and by consequence cost of transaction) and making it profitable for the sequencers to participate. Further considerations need to be made for fork choice rules, parallel proofs and economical incentives.
Example for the the middle of the spectrum is Leader with one or multiple backup leaders and/or falling back to partial or complete free for all if everyone else fails.
On a high level the Leader Election end of the spectrum trades off lowered transaction throughput and compromised liveness, for capital efficiency and low transaction costs. Free for all, chooses low capital efficiency and possibly high costs, but gains high throughput and availability.
Prover Choice
Similarly to sequencers, “Leader Election” sees a single prover being elected and be known ahead of time (preferably known only by the prover himself) to prove a certain sequence. If a single leader election is chosen, the main follow up topics of the design that need to be considered have to do with accounting for liveness of the leader. Keep in mind that the workload of provers is high and the time to produce proof is lengthy, which greatly exacerbates the problem of inactive leader. This, however does not necessary stall the network, only its finality. The downstream consequences of finality being stalled impact L1 and cross rollup communication, but the rollup itself can remain operational.
“Free for All” sees no single leader being elected and all actors can produce and submit proofs. If “Free for All” is chosen, the main consideration is capital efficiency - cost of participating as prover (and by consequence cost of transaction) and making it profitable for the provers to participate. In a sense this choice resembles Proof of Work algorithms. Further considerations need to be made for fork choice rules, parallel proofs and economical incentives.
A middle ground in the spectrum would be choosing one leader, one or multiple backup leaders and/or falling back to partial or complete free for all if everyone else fail.
Note: The choice if a single sequence and a single fork choice is being proven at one time is subject to other design choices outlined below.
On a high level the Leader Election end of the spectrum chooses possibly slow finality, but gains capital efficiency and low cost. Free for all, chooses low capital and resource efficiency likely resulting in high transaction costs, but has superior finality time.
Explicit Sequencer-Prover Coupling
In the case where the designer has not chosen complete “Free for all” on the “Prover choice” decision, they gain the option to chose to give the leader election rights to the sequencer(s). This effectively couples Sequencer(s) and Prover(s).
The “No Coupling” end of the spectrum disables the ability for the sequencers to choose their provers. The “Hard coupling” end of the spectrum allows any sequencer submitting a sequence to choose the prover eligible to prove it. A middle-ground option would be the sequencer choosing multiple eligible provers.
“No coupling” has no further impact on the throughput, availability and efficiency of the system. “Hard coupling” introduces the possibility to slow the finalisation of system via liveness problems, however leads to even greater system efficiency.
The increased capital efficiency for the system comes due to two factors. Firstly, due to the actors being able to synchronise offchain ahead of time. Second, because there is no implementation overhead for the L1 to implement “leader election” for provers.
Hard coupling becomes, especially relevant in Unlimited forks + Multiple Proofs (outlined bellow) based system where the prover election overhead and proof competition is multiplied by the number of forks.
Allowing Forks
Note: This choice is tightly related to the decision of the “Sequencer choice”. If the choice of the designer is to have a single leading sequencer, then no forks are possible and this design decision is not applicable. Anywhere else in the spectrum of “Sequencer choice” the designer will need to evaluate and make the decision of allowing forks.
“No fork” choice in Free for All or some other in-between design choice for “Sequencer choice” leads to eligible sequencers competing to be the first one to propose sequence to the L1. This sequence is considered the fork choice and the subsequent eligible sequencers need to build on top of it. Keep in mind that the proposed sequence might be invalid, and the subsequent sequencers will need to build further the chain, without applying state modifications of this sequence knowing that it is invalid.
Unlimited fork choice sees all eligible sequences submitted by eligible sequencers being treated as possible fork choices. Designers choosing Unlimited fork choice need to embed rules for choosing the canonical fork which subsequent eligible sequencers can use in order to know which chain to build upon. Furthermore the designers choosing unlimited fork need to consider the crypto-economical incentives for sequencers to participate even when their fork is not chosen to be the canonical one.
A middle ground would be allowing the submission of more than one fork but capping it to some number of forks. In this case the designer still need to embed the rules for choosing the canonical fork choice to build upon (f.e. using the valid fork of the sequencer with the highest posted bond).
In case of Free For All submissions of sequences, “No fork” choice decision leads to capital inefficiency from the perspective of the sequencer as multiple sequencers will be competing for a single slot. PBS systems will force competing sequencers to do bid wars and outbid themselves leading to lower revenues. “No fork” choice, however, simplifies the design by giving a single criterion for fork choice.
Unlimited fork choice lead to another type of capital inefficiency as multiple sequencers might be proposing the same or very similar fork. At the end one of these needs to be chosen, however the rest of the sequencers still might be considered for compensation. However, Unlimited fork choice enables high transaction throughput and availability for the rollup.
Number of Forks Proven
Note: This choice is tightly related to the decision of the “Allowing Forks”. If the choice of the designer is to have a single fork, then only one possible fork is there to be proven and this choice is not applicable. Anywhere else in the spectrum of “Allowing Forks” the designer needs to choose their approach towards proving forks.
“Unlimited forks” choice for the “Allowing Forks” consideration, or limited version of multiple forks choice leads to the existence of multiple possible forks for the rollup. The designer needs to choose whether to enable proving only the canonical fork choice (in accordance with the embedded fork choice rules) or enable proving multiple forks, even if they are possibly not going to be used.
“Single Fork Proofs” sees only the canonical fork being eligible for proving, unless proven invalid. Depending on the “Prover choice” decision one or multiple provers will produce proofs for the validity/invalidity of the canonical fork. The subsequent forks can act as backup forks until a valid fork is found.
“Multiple Fork Proofs” sees all the forks as being eligible for proving. Depending on the “Prover choice” decision one or multiple provers per fork will produce proofs for the validity/invalidity of the canonical fork.
Important consideration is that the proof generation work is very costly and needs to be incentivised either directly or indirectly. This means that there is a scenario where the design needs to account for incentivising for payment of the proof generation for forks that are never used.
A middle ground choice could be, using a “single fork proofs” choice for the initial canonical fork, but if it is proven invalid, to fallback to “Multiple Fork Proofs” to find the actual next valid fork.
“Single Fork Proofs” choice can lead to slower finality of the rollup. If the canonical fork is invalid, it will take more time and resources for the network to be able to move to the next one. In extreme cases there might be multiple invalid fork choices that are selected as the canonical (or secondary) fork choices in accordance with the fork choice rules and this will progressively increase the time to finality. This choice, however, leads to no unnecessary waste of resources for the provers and only the necessary proofs are generated and submitted.
“Multiple Fork Proofs” choice can lead to capital inefficiency and increased costs. The resources to prove all forks, including the unnecessary ones, will be spent by the provers and will have downstream consequences on the transaction prices. This choice, however, leads to the fastest finality as all fork choices are proven “in parallel” and invalid canonical forks do not slow down the finality (the rollup can just move to the first valid fork).
Synchronous vs Asynchronous Proofs
Lets consider the rollup as a chain of slots. In each slot there are one or multiple sequences, depending on the designer decision for "Allowing Forks”. The sequence(s) in the slots are building on top of the resulting rollup state (proven or not) of the chosen canonical fork (read sequence) of the previous slot. We can consider a slot finalised if there is a valid sequence that is chosen to be the canonical fork in accordance to the fork choice rules, proof for this sequence is submitted and all the slots before are finalised.
The design choice that the designer needs to make is whether to enable submitting and processing proofs only for the first not finalised slot or enable the provers to be submitting further down the chain for sequences in slots that are based on other still to be finalised slots.
The “synchronous proving” end of the spectrum sees the rollup only accept proofs for sequences in the first non-finalised slot.
The “asynchronous proving” end of the spectrum sees the rollup accept proofs for sequences in any non-finalised slot in the future.
Synchronous proving guarantees that no time finalisation gaps appear in the rollup chain of slots. This choice, however, opens the system finalisation to be bottlenecked by the throughput of L1. Furthermore it requires the provers to be monitoring much closer the L1 and the mempool in order to correctly time the submission of proofs.
Asynchronous proving, allows the provers to “fire and forget” any proofs they have generated thus virtually ensuring that whenever the finalisation of the canonical chain in L1 catches up with this slot, it will be able to instantly finalise it and move on. It however opens up the possibility for finalisation gaps on the canonical chain of the rollup. Any gap delays the finalization of the canonical chain of the rollup, regardless of all the proofs submitted for future slots. Furthermore it complicates the L1 onchain rules for finalisation of the canonical rollup chain introducing complexity for the system.
Last but not least, depending on the choices (will come to this later) in the crypto economical incentives decisions, gaps can decouple the payment associated with fork/slot finalisation and the submission of its proof. This opens up various smart contract related attack vectors for the rollup (f.e. need to design around traversing the chain of non-finalised blocks searching for possible next finalised one).
In a nutshel, synchronous proving is safer and easier to implement, but opens up the door for delayed finalisation. Parallel proving optimises for time to finalisation, however, it requires smart contract related attack vectors to be mitigated and introduces practical development and crypto economical complexity for the system.
Incentives
Sequencers Incentives
Generally the speed and quality of service of the sequencers is directly tied to the speed and quality of the rollup. The faster the sequencers act, the faster the rollup can advance (despite not being proven). However, due to the nature of the rollups, the sequencers are ultimately unchecked until a proof of validity/invalidity is submitted.
Two major intertwined decisions need to be taken by the designers: 1) When and how are the sequencers rewarded for correct behaviour and 2) When and how are the sequencers punished for misbehaviour.
Sequencer Rewards
Two types of design choices exist for the sequencer payment - early and late payment.
Early payment sees the sequencer being rewarded for their behaviour as soon as they submit a sequence. This reward can be static - a fixed reward per batch - or dynamic - based on the size of the batch. Fixed reward incentivises the sequencers to commit small batches as early as possible. Dynamic reward incentivises the sequencers to try and produce the biggest sequence possible, in order to amortise the L1 cost for commitment.
Late payment sees the sequencer being rewarded once their sequence has been proven valid. One option for this is making the sequencer to be the coinbase of the L2 blocks of this sequence, but this decision needs to be taken into consideration together with the decision for “Allowing forks”. Another option is to provide external crypto economical reward either in L1.
Early payments are somewhat safer and more capital efficient for sequencers - they do not need a huge inventory to cover the L1 tx costs, except in some designs they might need a way to exchange the received reward for ETH. Early payments, however introduce systemic risks through misbehaviour, that needs to be addressed via concrete sequencer punishment mechanisms.
Late payments decouple the cost and reward for the sequencers in terms of time - they pay the L1 cost early, but get the reward later. This leads to them requiring bigger inventory and therefore can lead to increased costs for the system. Late payments, however, are safer for the system as the sequencers are ever only paid when behaving correctly.
Sequencer Punishment
Sequencer punishment can range from “No punishment” to “Slashing”.
No punishment sees the sequencer misbehaviour being left unpunished apart from the L1 tx costs spent by them.
Slashing sees the sequencer being required to stake, either one time, or per sequence and have their stake slashed for misbehaviour.
No punishment is easier to implement, but is incompatible with early sequencer payment design choice. Furthermore, it opens up the system to sybil attacks depending on the choices around “Sequencer choice” and “Allowing Forks”.
Staking, is harder to implement and balance out, as requires further capital upfront for sequencers. Furthermore it can lead to increased costs for the rollup as “premium” for the sequencers needing to get upfront capital. Staking, however, adds security and safety to the system as the sequencers have a tangible skin in the game.
Prover Incentives
Generally the speed of finalisation of the rollup state is directly tied with the incentives of the provers to act quickly. Provers work, however, is normally very resource and time consuming. Keep in mind that the provers cannot really misbehave, as the ZK proofs technology gives us the guarantees that something either is valid, or unverifiable.
The major design decision that the designer needs to make is how and when to pay to the prover for their work.
Prover Payment
Provers payments can range from getting a submission payment or coinbase payment.
Submission payment sees the prover being awarded either a fixed or dynamic amount when they submit a proof that is successfully verified.
Coinbase payment sees the prover being awarded the transaction fees from this sequence.
Fixed submission payment is easier to implement, however it might lead to sequences where the payment is not sufficient for the provers to do the work.
Dynamic submission payment increases the complexity, mainly due to the logic of determining the payment size.
Coinbase payment is easiest to implement, but again might lead to sequences where the payment is not sufficient.
Further Design Notes
Multi-rollup Ecosystem and Shared Infrastructure
A popular theme in the rollups design space is the creation of rollup stacks - enabling developers to launch their own rollup based on existing technology (ex. OPStack). A popular option for these forming ecosystems is to use the notion of “Shared Sequencer” between multiple rollups.
It is important to note, that while the sequencers are shared, if the shared sequencer is a single entity then the same centralisation vectors to the ones of a single rollup apply. In this sense, whether it is a single rollup or ecosystem of rollups, the evaluation framework above applies at a macro level.
Example Designs
In order to illustrate better the usefulness of the described analysis framework, here is a fictitious rollup design made according to the design decisions outlined above. This design is extreme example that should not be taken as prescription and has obvious and glaring downsides.
The super-high throughput rollup - detailed
A designer designing a rollup optimising for super-high transaction throughput can start by selecting completely permissionless “Free for All” manner for “Sequencer Choice”. This will allow sequencers to complete to submit sequences in L1 as early as possible. To further foster this behaviour, the designer can choose “early fixed payment” in the “Sequencers Reward” choice and “No Punishment” in the “Sequencers Punishment” section.
In order to somewhat mitigate the impact on transaction costs, the designer can choose “Leader Election” for “Prover Choice” and further optimize for it via “Hard Coupling” the sequencer and the prover.
The designer can choose to enable “Unlimited forks” for the “Allowing choice” decision, adding more assurances that the system will be optimised for throughput. In order to somewhat offset raising costs, the designer can choose to enable “Single Fork Proofs” for “Number of Forks Proven”. This, however, negatively impacts the time to finalization.
In order to somewhat offset the raising transaction cost of the system, the designer can enable Synchronous proving for the slots.
Lastly, the designer can choose dynamic payment for provers in order to ensure the eventual finalization of the rollup chain.
While extreme, this example makes all the tradeoffs to ensure the very highest transaction throughput, and makes an effort to keep the transaction costs somewhat down.
The low transaction costs rollup - brief
- Sequencer Choice: Leader Election + Backup Leader
- Prover Choice: Leader Election + Free for All
- Sequencer-Prover Coupling: Hard Coupling
- Sequencer Rewards: Early Fixed Payment
- Sequencer Punishment: No Punishment
- Prover Reward: Coinbase Payment
- Allowing Forks: No Forks
- Number of Forks Proven: Single Fork
- Synchronous vs Asynchronous Proofs: Synchronous Proofs
Conclusion
The design space for decentralisation of rollups is vast and many areas of it are still unexplored. This analysis framework attempts to help designers and evaluators to navigate it and establish the cause and effect relationships between the various design choices available.
Authors & Contributors: George Spasov (george@limechain.tech), Daniel Ivanov (daniel@limechain.tech)