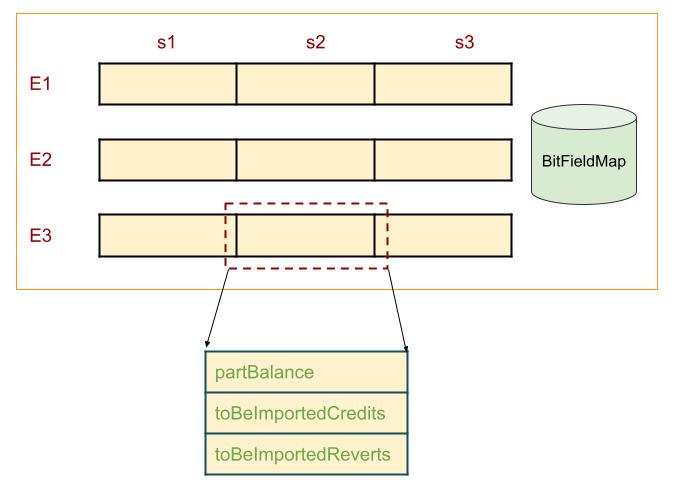
My previous approach extended the netted balance approach for user-level ETH transfers. The netted balance approach distributes the balance of a specific EE on a specific shard to all shards, by storing a portion on every shard.
The main purpose of this refinement is to solve the problems of the previous approach and thereby gain atomicity.
The core idea of this proposal is to extend the idea of distribution of EE-balances to outstanding user-level credits and outstanding user-level reverts. The netted state (extends the netted balance) is used as a channel to communicate outstanding credits to recipient shard and outstanding reverts to the sender shard.
Preliminaries
- s_i's denote shards.
- E_i's denote execution environments.
- a_i, b_i's denote users.
- System Event messages are similar to application event messages in contract code, but are unforgeable by the application. We have one System Events: ToCredit. It includes sender details (shard-id, EE-id, user address), recipient details, transfer amount. It also includes the block number of the shard block where this event is emitted, and an index number starting from 0 (for every block).
Transaction Types
- Cross-shard debit transfer
- a_i \stackrel{x_i}{\Longrightarrow} b_i, cross-shard transfer of x_i ETH from the user a_i on (s_1,E_1) to the user b_i on (s_2,E_2).
- Signed by the sender a_i. Signature is stored in the fields v, r and s as in Ethereum 1.
- Submitted on sender shard.
- Contains a unique transaction identifier.
- Emits a ToCredit System event on success
- Cross-shard credit transfer
- a_i \stackrel{x_i}{\longrightarrow} b_i, credit transfer of x_i ETH to b_i on (s_2,E_2), which is from a_i on (s_1, E_1).
- Submitted on recipient shard.
- Includes the ToCredit System Event and the Merkle Proof for it.
Algorithm for Block Proposer
WLOG assume that a Block Proposer (BP) is proposing a block numbered k on shard s_1. Then BP executes the following algorithm for every EE E_i.
- Obtain realState(s_1, E_i).
- Ensure that the obtained s_i.partState from shards s_i, 1 \le i \le n are correct using Merkle Proofs and crosslinks
- realBalance$(s_1,E_i) = \sum_i s_i$.partState[s_1,E_i].balance;
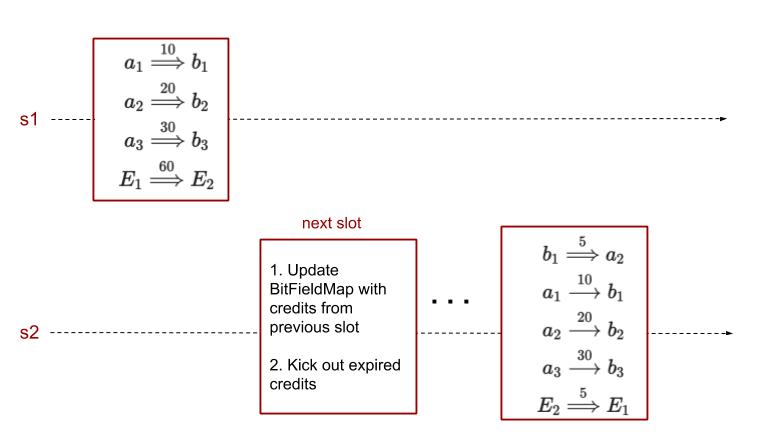
For every s',E', net(s',E') = 0; - Update BitFieldMap
- Add entries for outstanding credits:
[s', E', (k-1)] \mapsto {e \mapsto 0 | e \in \bigcup_i s_i.partState[s_1,E_i].credits} - Kick out expired credits: If there is an entry with [s',E',key] such that key + timeBound == k
- s_1.partState[s',E'].reverts = { e | (e \mapsto 0) \in BitFieldMap(key) AND sender(e) \in (s',E') }
- Delete the entry with key
- net(s',E') = \Sigma_e ~x_e where e \in s_1.partState[s',e'].reverts and x_e denotes transfer amount
- Add entries for outstanding credits:
- Process user-level reverts
- reverts = \bigcup_i s_i.partState[s_1,E_i].reverts
- for each t_i \in reverts
- sender(t_i).balance += x_i
- For every pair (s_2,E_j)
- Select transactions t_1...t_n to be included in the block
- s_1.partState[s_2,E_j].credits = \emptyset; ~~s_1.partState[s_2,E_j].reverts = \emptyset;
- For every i in 1 … n:
- If t_i : a_i \stackrel{x_i}{\Longrightarrow} b_i AND realBalance(s_1,E_i) > net(s_2,E_j) + x_i
- include t_i to the block
- if t_i executes successfully
- balance(a_i) -= x_i (implied with successful execution of t_i)
- net(s_2,E_j) += x_i
- emit ToCredit(a_i, x_i, b_i) System Event
- s_1.partState[s_2,E_j].credits ~ \cup= ~ {t_i};
- Else if t_i : b_i \stackrel{x_i}{\longrightarrow} a_i AND Merkle Proof check of ToCredit System Event passes AND realBal(s_1,E_i) > net(s_2,E_j) + x_i
- if expired(t_i) OR BitCheck(t_i) fails
- delete t_i from transaction pool
- else
- include t_i to the block
- SetBit(t_i);
- if t_i executes successfully
- bal(a_i) += x_i; (implied with successful execution of t_i)
- if failure
- s_1.partState[s_2,E_j].reverts ~~\cup=~ {t_i};
- net(s_2,E_j) += x_i
- if expired(t_i) OR BitCheck(t_i) fails
- If t_i : a_i \stackrel{x_i}{\Longrightarrow} b_i AND realBalance(s_1,E_i) > net(s_2,E_j) + x_i
- Update EE-level transfer
- s_1.partState[s_1,E_i].balance -= net(s_2,E_j);
- s_1.partState[s_2,E_j].balance += net(s_2,E_j);
Remarks
- Before processing a pending cross-shard credit transfer transaction b_i \stackrel{x_i}{\longrightarrow} a_i, the EE-level transfer is already complete.
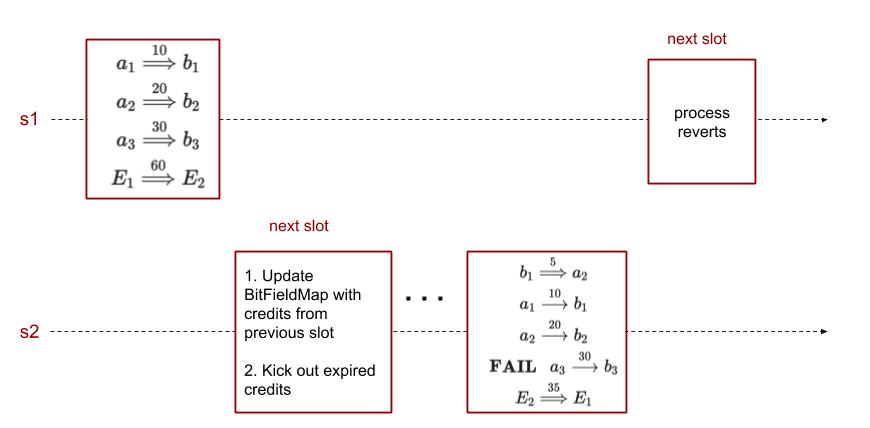
- User-level reverts happen in the immediate next slot after a failed or expired credit transfer. The EE-level revert happens in the same slot as the failed / expired credit transfer.
- Transaction identifiers need to be unique inside the time-bound
- There is a corner case where the sender disappears by the time revert happens, then we end up in a state where there is ETH loss at user-level, but not at EE-level. This appears to be a correct state when such a situation happens.
- A transaction is not included in a block if the EE does not have sufficient balance. Note that EE balance check is done even for credit transfers because of potential reverts.
BitFieldMap
The datastructure BitFieldMap is stored in the shard state to protect against replays of credit transfers and to time-out credit transfers. It is a map from a block number to a set of elements of the form (t_i \mapsto b_i), where the block number identifies the block on the sender shard where a cross-shard debit transfer t_i happened, and b_i is a bit initially set to 0.
- BitCheck(t_i) returns true when there is (t_i \mapsto 0) for any block number. Because transaction identifiers are unique, a transaction appears only once in BitFieldMap. Zero indicates that the credit is not processed yet. One indicates that the credit is already processed. If no entry is present, then this is an invalid credit and false is returned.
- SetBit(t_i) sets the bit for t_i to 1 for the block number that is already existing.
A timeBound is required to kick out long pending credit transfers. The second bullet of step 3 describes this procedure. The idea is to move the expired user-level credit transfers as user-level reverts on the sender shard, and achieves a fixed size for BitFieldMap.
Processing Revert Transfers
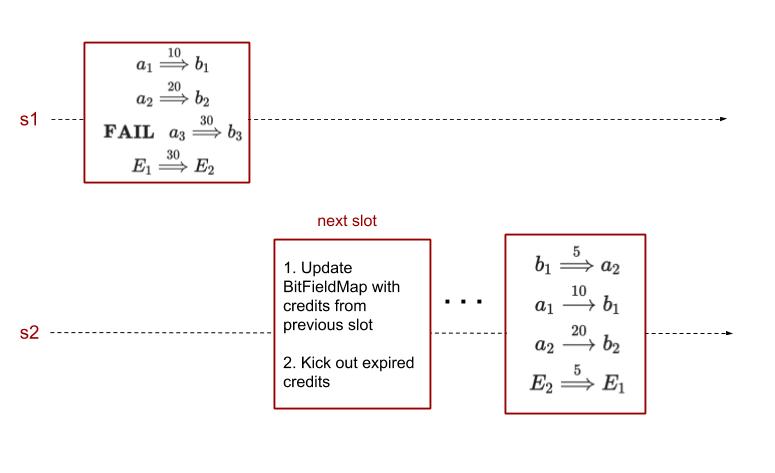
A revert transfer is placed in the shared portion of the EE-level state when either the corresponding credit transfer fails or expires. It is stored in the local shard state, but in the portion that is reserved for the sender shard. The step 4 collects all the portions and processes the user-level reverts.
Note that the EE-level revert happens on the recipient shard in the same block where the credit transfer fails or expires. However, the user-level revert happens in the very next slot on the sender shard. This technique pushes the revert to the EE host functions instead of treating them as separate transactions. This avoids complex issues like revert timeouts and revert gas pricing.
Benefits
- No locking / blocking.
- No constraint on the block proposer to pick specific transactions or to order them.
- Atomicity
Demerits
In every block, a BP has to get the outstanding credits and reverts from every other shard. This is inherited from the netted balance approach, where a BP requires the netted balances from all shards. However, it is restricted to the sender EE’s that are derived from the user-level transactions included in the block. The problem is aggravated here, because we would need to request from all EE’s, even for the EE’s not touched in this block.
Examples
Optimistic case
When Debit fails
When Credit fails
Future work
- Optimise the space requirement for storing outstanding credits and outstanding reverts.
- Explore caching for optimising the reads of partStates of every EE of every other shard in every block (related to the above mentioned demerit).
Thanks @liochon @prototypo @drinkcoffee for all your comments / inputs.