By @sarisht @kartik1507 @voidp @soispoke @Julian
In collaboration with @barnabe @luca_zanolini @fradamt - 2024-09-12T04:00:00Z
TLDR;
In this post, we introduce an AUCtion-based-Inclusion List design, AUCIL, that leverages competition within an inclusion list committee consisting of rational parties. The protocol design leverages two key components: (i) an input list creation mechanism allowing committee members to pick non-overlapping transactions while maximizing their fees, and (ii) an auction mechanism allowing parties to ensure most of these input lists are included in the final output inclusion list. The former ensures many censored transactions are considered for inclusion, and the latter employs competition where including as many of the input lists as possible is incentivized to produce the output inclusion list.
Introduction
The centralized builder ecosystem of Ethereum today has led to ~2 builders with the power to decide which transactions are posted on Ethereum. This centralization leads to censorship concerns since the builders have complete authority over which transactions are included. The current solution proposed (and rejected) by Ethereum (EIP 7547) requires the current proposer to determine the inclusion list (or the set of censored transactions) to be included by the next proposer. Such a proposer also acts as a single point of failure, which can easily be bribed to exclude transactions. This has led to proposals such as COMIS and FOCIL that require inputs from multiple proposers to be aggregated to form the inclusion list.
Intuitively, using multiple proposers implies the need to bribe multiple parties for a transaction to be excluded. However, do all parties include the transaction in the first place? Since the resulting inclusion list is finite (limited to block size), how do each of these parties decide which transactions to include in their local list such that maximizing the utility also increases the system’s throughput? Moreover, when aggregating the transactions to produce the inclusion list, how many points of failure can be bribed to exclude transactions? This post introduces a multi-proposer design called AUCIL to address these questions.
Motivation
Let’s first motivate the first part as to how the inclusion lists should be created. For existing inclusion list designs, the intricate assumption is that an IL Proposer can include as many transactions as it sees. While FOCIL or COMIS, leave the proposal of transactions in Local Inclusion List underspecified, Fox et al. assumes that there is no network congestion. However, including all the transactions could lead to a scenario where the size of the inclusion list is larger than the block size. In such a scenario, the builder (constrained by transactions in the Inclusion List) would add as many transactions as possible, dropping any leftover transactions in the inclusion list.
The first thing to note above is that for an IL Proposer, it never makes sense to add more transactions than the block size, and thus, there could be an implicit block space size constraint (\mathcal{L}) on the Local Inclusion List (We would refer to these as Input Lists).
Now, consider that the proposer is passive (i.e., rational but does not accept a bribe). Since each input could be size \mathcal{L}, the resulting union of lists could be of size \geq \mathcal{L}. Now, the builder (or proposer without the PBS) is constrained to pick transactions from the Inclusion List; it would pick the top \mathcal{L} paying transactions, and the rest would not execute. Thus, the inclusion list proposers would only want to include the top \mathcal{L} transactions. Thus, all the previous analysis made for inclusion lists with a scale factor of the number of inclusion list proposers holds in this case (Fox et al., FOCIL, COMIS).
However, things look very different in the presence of a bribing adversary. Consider that one party is bribed enough (we will quantify this at the end of paragraph) to exclude a top \mathcal{L} paying transaction and instead replace it with (\mathcal{L}+1)^{th} transaction. The builder now receives an inclusion list with \mathcal{L}+1 transactions and can choose any transaction to exclude. The adversary can further bribe the builder to exclude the target transaction. Since there is one extra transaction in the list, the block can be formed without violating the properties of an inclusion list (All transactions are executed, or the block space is full). Coming back to the incentives for the party, if it is the only party that deviates from picking top \mathcal{L} transactions, then it would be the only recipient of the fee from (\mathcal{L}+1)^{th} transaction. This may be larger than the utility received (if f_t for the target transaction is not n times larger than f_{\mathcal{L}+1} for the inserted transaction). Even in the worst case, the bribe required would be slightly larger than f_t/n.
All in all, the property of inclusion list that allows the transaction to be excluded if the block is full is a property the design in this post wishes to avoid. Thus, we would restrict the size of input lists to less than \mathcal{L}/n such that even if all parties propose unique transactions, the size of the inclusion list is less than the available block size.[1]
There could exist other solutions to this problem like cumulative non-expiring inclusion list and unconditional inclusion lists, however, these require additional state support, where parties would have to keep track of previous inclusion lists.[2]
As for the other question of how many points of failure exist while using multi-proposer designs, aggregation of lists from all parties is the most critical point of failure, which hasn’t yet been adequately studied. Fox et al. sidestep this by never truly aggregating and assuming that the proposer’s inputs would be included without truly analyzing the problem. In COMIS, the aggregator role is formalized, and they assume that this role is trusted for their analysis. FOCIL removes this assumption by using the proposer of the next block and keeping the point of failure in check with the committee of attesters. However, relying on attesters comes with its share of problems. Attesters are not incentivized to verify; as long as they vote with other attesters, they receive rewards without the risk of a penalty. Using attesters to compute is thus more unreliable than relying on the attesters to confirm the existence of the block or verify a proof as used in this post.
Model
In this post, we consider all parties involved in consensus as rational, i.e., trying to maximize the value they receive through transaction fees, consensus, or bribery. We will call each party collectively proposing the inclusion list as an IL Proposer and their input as an input list. We will refer to the aggregator as the party that computes a union of these input lists to create an inclusion list. Differing from previous proposals, we assume that the input list size of each party is constrained. The size of an input list can be at most k \leq \mathcal{L}/n, as mentioned in the previous section. The total number of IL proposers is considered to be n. Each transaction tx_i pays a fee of f_i for inclusion in the inclusion list, which is paid to the IL Proposer(s) that include it (chosen by the user independently from the base fee and Ethereum transaction fee). If the transaction repeats across multiple input lists, the fee is equally divided amongst all the IL Proposers that included it tracably on-chain.
We assume an external adversary with a budget such that it can bribe parties to take adversarial actions.
Problem Statement
The problem setting consists of n rational parties who locally have access to a set of censored transactions (M_i) that are continually updated (their mempool). Let M = \cap_i M_i. The problem is to create a list of valid transactions with each party contributing a share of transactions it observes.
Adversarial model. We assume each of the n parties is rational, i.e., they maximize their utility. We assume a bribing adversary will bribe these parties to censor one or more transactions.
Definition ((b,p,T)-Censorship Resistance.) We say that a protocol is (b,p,T)-censorship resistant if given a budget b to an external adversary for bribing parties, for all transactions t \in T(M) at least p parties output a list which contains all the transactions in T(M).
The protocol design aims to maximize b for a fixed p and |T(M)|. More concretely, in non-multi-proposer inclusion list design schemes, b is typically O(f), but our protocol aims to obtain b = O(n\cdot f).
To facilitate understanding of the goal, T(M) can be considered the “feasible” subset of transactions in M, e.g., those paying sufficiently high fees subject to a space limit. The definition of T depends on the protocol we implement, and it is justified why such a T is used.
In our protocol, we assume that M_i = M. When M_i \neq M, our protocol does not satisfy the definition since it may output a higher paying transaction that appears in some M_i at the expense of some lower paying transaction in the intersection
Input List Creation Mechanism
The first question we address is how IL Proposers select transactions for their input lists. A simple approach is for IL Proposers to naively choose the transactions that pay the highest fees, regardless of the actions of others. However, this greedy approach is not a Nash equilibrium. If all other IL Proposers are greedily selecting transactions, the rational choice for any IL Proposer might not be to do the same. Table 1 illustrates this point.
| Strategy | Objects Picked | Utility |
|---|---|---|
| Pick Top Paying | (o_1,o_2) | 7 |
| Alternate | (o_3,o_4) | 15 |
Table 1: Picking top-paying objects is not a Nash equilibrium. Consider transactions (\{o_1,o_2,o_3,o_4,o_5,o_6\}) with utilities (\{11, 10, 9, 6, 4, 3\}) respectively and three players with max size input list of 2. Other players are assumed to follow the strategy of picking the top-paying transaction.
A more viable approach is to use mixed strategies, where each party selects transactions based on a predefined probability distribution. Deviating from this distribution would result in lower expected revenue. However, a mixed Nash equilibrium may not be sufficient, especially in games where players can wait to observe others’ actions before deciding. Thus, this post explores a correlated equilibrium instead.
A correlated equilibrium is a situation where each player is suggested specific actions, and deviating from these suggestions leads to lower utility, assuming others follow the suggestions. To prevent centralization (by asking a single known party to send recommendations), we propose a well-known algorithm that each party can run locally to simulate these suggested actions. Deviating from the algorithm would result in lower utility for the deviating party.
Algorithm 1: A Greedy Algorithm for Transaction Inclusion
Input: ( n \geq 0 ), ( m \geq 0 ), ( k \geq 0 ) (number of players, transactions, input list size)
Output: ( L_i ) arrays for all ( i \in P ) (final inclusion lists for each player)
- P \gets [1,\dots,n]
- U \gets [u_1,\dots, u_m]
- N \gets [1,\dots,1]
- \forall i \in P: L_i \gets [1,\dots,1]
- l \gets 0
- while l < k do
- i \gets 0
- while i < n do
- U_{curr} \gets (U \otimes L_i) \oslash N
- s \gets argmax(U_{curr})
- L_{i}[s] \gets 0
- N[s] \gets N[s] + 1
- i \gets i + 1
- end while
- l \gets l + 1
- end while
- return \forall i \in P: L_i
This algorithm iteratively updates each player’s transaction inclusion status. Each player’s input list (L_i) indicates whether a transaction has been included (0) or not (1). The algorithm aims to maximize utility values greedily, including transactions based on their current utility and the number of times each transaction has been included.
Description of the algorithm
Consider the following simulation protocol. All parties are first numbered randomly. Since the randomness needs to be the same across all parties, a random seed is agreed upon before the start of the protocol. All parties are assigned items greedily, one at a time. Each party picks the item that gives the maximum utility at that instant. To do so, it computes the current utility of all objects yet to be chosen \left((U \otimes L_i) \oslash N\right). The first (U \otimes L_i) makes the utility of all objects already chosen by i as 0, and then \oslash N divides by the number of parties sharing the object if party i decides to pick that object. The list of objects the party picks is updated (0 implies the object is chosen), and the number of parties picking the object is also updated. The procedure is repeated k times such that each party picks k objects. This protocol achieves a correlated equilibrium. Note that while the protocol assigns objects to parties one at a time, in practice, the output recommends all transactions to the parties at once.
This protocol provably achieves a correlated equilibrium while also achieving a notion of game-theoretic-fairness properties (almost equal distribution of fee) (Paper to follow soon). The set of all transactions chosen by the input list creation algorithm is T(M), for which we achieve (b,p, T)-censorship resistance through AUCIL, which follows.
Aggregation of input lists
After creating input lists, the next step is to aggregate the lists to create an inclusion list for the next block. If a transaction appears in the inclusion list, it is constrained to appear in the next block. Since the space occupied by the input list is fixed, it cannot suffer from spam transactions since each transaction is confirmed valid (with an adequate base fee) right before the block that includes it.
A standard way to approach this problem is to assign a party the role of an aggregator. This aggregator would compute the union of all the input lists and add it to the inclusion list. However, this aggregator is now a single point of failure. For instance, it may be the case that the aggregator may not receive input lists from all IL proposers and thus cannot be expected to add all input lists. However, if we consider this and only require it to include some threshold number of input lists, then the aggregator can strategically omit specific input lists and significantly reduce the required budget to censor transactions.
So, what can be done in this case? FOCIL requires the proposer of the following block to include an inclusion list, a superset of local input lists. However, it still allows for some transactions to not be on the inclusion list (due to the threshold). Instead, we look at a different way to deal with this problem. We auction off the role of the aggregator; however, instead of paying a bid to win the role of the aggregator, the bids are the size of the inclusion list. Thus, if a party P proposes a larger inclusion list than all other parties, then P would be rewarded with the aggregator role and reward.
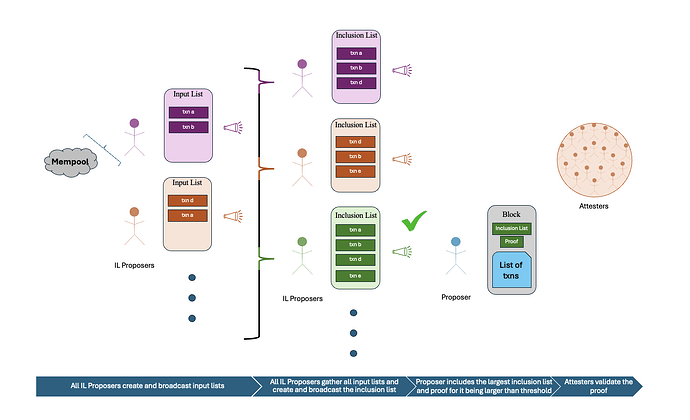
Algorithm: AUCIL Outline
Participants: All IL proposers P_1, P_2, \ldots, P_n
Step 1: IL Proposers Broadcast Input Lists
- For each proposer P_i:
- P_i \rightarrow_B (broadcasts to all parties): \text{inpL}_i
Step 2: Parties Aggregate Input Lists into an Inclusion List and Broadcast It
- For each party P_j:
- \text{incL}_j = \bigcup_{i=1}^{n} \text{inpL}_i
- P_j \rightarrow_B (broadcasts to all parties):\left(\text{incL}_j, \ell_j = \text{size}(\text{incL}_j)\right)
Step 3: Proposer Selects the Highest Bid Inclusion List
- Proposer receives: \{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\}
- Proposer selects the highest bid.
While Step 2 has its incentives clear by introducing aggregation rewards (u_a), Step 1 and Step 3 are not incentive compatible. If all other parties broadcast their input lists, then it is dominant not to broadcast its input list for a party. This way, it can create the largest inclusion list and thus win the auction. Thus, Step 1 is not incentive-compatible. Similarly, the proposer is not incentivized to pick the largest bid. Censorship in auctions (Fox et al.) has been studied and is easily applicable here. Thus, Step 3 is also not incentive-compatible.
Recall the definition of censorship resistance. If some protocol satisfies the definition of (b,p, T)-censorship resistance, then at least p parties output a non-censored inclusion list. Thus, we require the proposer to include proof of the included bid being greater than n-p other bids (e.g., including n-p bids). If the proposer fails to add such proof, the block would be considered invalid, thus making Step 3 incentive compatible.
We make the auction biased to deal with the problem of not broadcasting. First, observe that if no party is broadcasting its input list, then the probability of winning the auction for any party is very low; thus, broadcasting its input list at least yields the rewards from including the input list in making the inclusion list. Thus, if more people believe that keeping its input list private does not lead to a significant increase in the probability of winning, then parties would be incentivized to broadcast its input list.
Algorithm: AUCIL
Participants: All IL proposers P_1, P_2, \ldots, P_n
Step 0: IL Proposers Generate Their Auction Bias
- For each proposer P_i:
- P_i generates a random bias: \text{bias} \gets \text{VRF}(P_i, \text{biasmax})
- (The bias is uniformly distributed between 0 and \text{biasmax} and is added to the bid.)
Step 1: IL Proposers Broadcast Input Lists
- For each proposer P_i:
- P_i \rightarrow_B (broadcasts to all parties): \text{inpL}_i
- (Proposers broadcast their input lists to all parties.)
Step 2: Parties Aggregate Input Lists into an Inclusion List and Broadcast It
- For each party P_j:
- \text{incL}_j = \bigcup_{i=1}^{y_j} \text{inpL}_i
- (where y_j is the number of input lists party P_j receives.)
- P_j \rightarrow_B (broadcasts to all parties): \left(\text{incL}_j, \ell_j = y_j + \text{bias}\right)
- (Parties declare their bid with the added bias.)
- \text{incL}_j = \bigcup_{i=1}^{y_j} \text{inpL}_i
Step 3: Proposer Selects the Highest Bid Inclusion List
- Proposer receives: \{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\}
- Proposer selects the highest bid and adds it to the block (\text{incL},\ell).
- Proposer adds proof that the highest bid is greater than n-p other bids.
Step 4: Attesters Vote on the Validity of the Block
- For each attester:
- Attester receives: \{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\} and (\text{incL},\ell)
- Attester verifies the attached proof and votes only if the proof is correct.
- Block is considered valid if it receives more than a threshold of votes.
With the above algorithm, we claim that the party is incentivized to broadcast the input list unless the bias drawn is greater than \text{biasmax} -1. Even when the bias is greater than \text{biasmax} -1, a mixed Nash equilibrium still exists, and parties could still choose to broadcast.
Censorship Resistance
Censorship by bribery to IL Proposers
The first attack step an adversary can take is removing a transaction from the input lists. For this, assume that a bribe is given to those IL Proposers who are assigned to include the target transaction. This bribe should be enough to ensure that the target transaction is excluded from each input list with probability 1. It is assumed (for now) that each of these IL Proposers would compute the union of all observed input lists in Step 3.
Fox et al. analyze the bribe required for a multi-proposer scenario. In their case, it is assumed that the transaction repeats across all proposers. If a transaction pays a fee (higher fee for them) of f_i, then the adversary would have to pay n times the fee to censor the transaction.
In our case, the analysis is similar. If the transaction repeats across \kappa_i input lists, then the expected bribe required is \kappa_i f_i. The parameter \kappa_i is directly proportional to \frac{n\cdot f_i\cdot k}{\sum f_i}, where \sum f_i is the sum of fees paid by all transactions chosen by the protocol. As an intuition for this number, one of our results ensures that the revenue distribution from each transaction is fair, and thus, assumes that each transaction gives the same utility. (Let’s say there exist two transactions paying a fee of 15 and 5, respectively, then the former transaction would be included in thrice as many input lists as the latter transaction. Thus, revenue is the same). n\cdot k represents the total available slots out of which a transaction with fee f_i would occupy \frac{f_i}{\sum f_i} off the total space to maintain the same revenue assumption. Thus, if bribing the IL Proposers to exclude the transaction from the input list is the dominant action (as compared to bribery by aggregator we will mention next), then the protocol would be (b=O(\frac{nkf_i^2}{\sum f_i}),n, T)-censorship resistant.
Censorship by bribery to aggregator
In an alternate bribery attack, the adversary could bribe a party to reduce its bid by excluding all input lists that contain the target transaction. Thus, the bid for each party decreases by \kappa_i. This would be the same as drawing a bias \kappa_i less than what is drawn. A bias of \text{biasmax}-1 is supposed to have almost 0 probability of winning, and thus, reduction of a party bias to \text{biasmax}-\kappa_i, essentially means the adversary is bribing the party to not participate in the auction. From our analysis, the adversary would have to pay in expectation \frac{\kappa_i n}{biasmax} parties (Each with a bias greater than n-\kappa_i) a bribe of u_a each in order for them not to include the input lists containing the target transaction. Setting \text{biasmax} and u_a to be \sqrt n and \sqrt n \cdot u_{il} \geq \sqrt n \cdot f_i, we achieve (b = O(\frac{n^2kf_i^2}{\sum f_i}),n-\kappa_i\sqrt n+1,T)-censorship resistant.
Conclusion
We outline an input list building scheme that all parties are incentivized to follow. Working within the confines of limited-size inclusion lists, we achieve significant censorship resistance guarantees (proportional to the number of parties, including the transaction). Then, we looked at an aggregation scheme, AUCIL, that utilizes auctions to incentivize parties to include the largest inclusion list. AUCIL ensures that the aggregator is incentivized to add all input lists to the transaction. We are also analyzing how coalition affects the censorship resistance guarantees and will publish the results soon. Meanwhile, it would be amazing to hear thoughts on AUCIL and the inclusion list building mechanism.
Note that with EIP-1559, the cost to fill the block scales when the block space is full. And so, if the network is not congested, and the adversary is inserting artificial transactions to raise the congestion, then the cost of bribery would be high across multiple blocks. ↩︎
We achieve the same “unconditional” property as Unconditional ILs without assigning exclusive Inclusion List space. ↩︎