Introduction
The design of Plasma MVP requires that many UTXOs be withdrawn within a relatively short period of time (in the worst-case scenario). The maximum number of UTXOs that can be safely withdrawn inherently bounds the transactional capacity of the MVP chain. Currently, most MVP designs only support exits of individual UTXOs. A significant portion of the gas used by these exits is the up-front constant transaction fee charged by the EVM.
We can reduce the marginal cost of each additional UTXO if we combine individual exits into a single larger exit. One proposal suggests a simple way to start multiple withdrawals by pointing to each UTXO in the withdrawal. This is already significantly more efficient than individual exits, but we can do even better.
The original Plasma paper suggests a mass exit protocol that represents UTXOs using a bitfield. We specify a basic protocol that makes use of this bitfield construction. However, the protocol is relatively unoptimized and there’s a lot of room for improvement. There’s a good chance parts of this don’t work at all in practice, so nitpicks and feedback are much appreciated! This post is intended to start the conversation around mass exits and see if we can design something better. Some open questions/areas of improvement are given later.
Background
Bitfields & UTXO Aggregation
Let’s quickly talk a little bit about bitfields. Generally, when we’re talking about bitfields for mass exits, the bitfield is sort of like a big pointer to a list of UTXOs. Each bit is pointing to a specific UTXO. This means we need some information about which UTXOs are actually being referenced. Once we’ve figured out this part, we just say that if a certain bit in the bitfield is set to 1, then that UTXO is being exited.
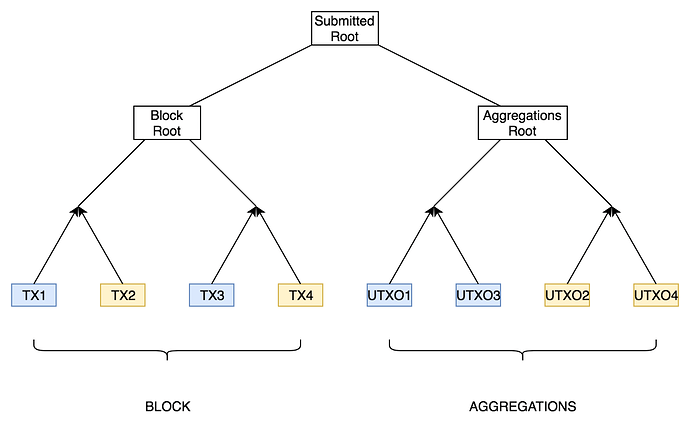
So how do we know what UTXOs are actually being referenced? Basically, we make use of something called “UTXO aggregation”. We require the consensus mechanism to aggregate UTXOs based on some metadata, combine these aggregated UTXOs into another Merkle tree, and publish the root of this tree along with the block root. The aggregation tree contains all outstanding UTXOs, not just the ones in the current block (the full UTXO set).
Here’s how that looks in practice:
For the sake of this example, each transaction creates a single UTXO.
TX1 and TX3 share some metadata, and TX2 and TX4 share some other metadata. The UTXOs created by these transactions are then aggregated based on the shared metadata. This might be a shared owner, a shared amount, or really anything else. The exact aggregation method used isn’t important. Users can coordinate in advance to figure out some optimal aggregation for their own UTXOs.
We rely on the consensus mechanism to actually create this aggregation. Therefore it’s possible that the mechanism aggregates UTXOs incorrectly. Even though funds can’t be directly stolen, malformed aggregations make mass exits more difficult (or even impossible). Clients should therefore be programmed to automatically exit if this attack is detected. The risk of a mass exit may also discourage the mechanism from engaging in this behavior.
Client funds are at risk if the aggregation is withheld. Therefore, clients should always exit if they detect withholding.
Conveniently, we also don’t need to query the aggregation tree. If the aggregation tree is properly computed, then we can pull the block, compute the aggregation tree ourselves, and check that the hash matches the published one. If clients ever detect an invalid hash, they should immediately exit.
We can now easily reference UTXOs with a pointer to a specific aggregation and an offset. We’re basically saying “this length N bitfield refers to the N UTXOs after index M in this set of transactions,” where the set of transactions is the set of leaves of some subtree of the aggregation tree.
Sum Merkle Trees
Part of our protocol requires that users be able to commit to the total value in the mass exit. We’re using something called a “sum Merkle tree” for this. Sum Merkle trees are basically just Merkle trees that commit to the sum of the leaves.
Here’s how that looks:
Each leaf node commits to a single UTXO and the sum of the value the UTXO and of every UTXO to the left of it. Each interior/root node commits to the all the data a normal Merkle tree would (represented by
...) as well as the greater of the nodes’ two child values. In a correctly constructed tree, a root node should therefore commit to the total value of each UTXO in the tree.
Detecting Invalidity in Merkle Sum Trees
We can only detect that a Merkle sum tree is invalid if we know the set of UTXOs at the bottom of the tree. Luckily, our aggregation scheme guarantees that the leaves are only not known if the aggregation tree is withheld, in which case the user should exit anyway.
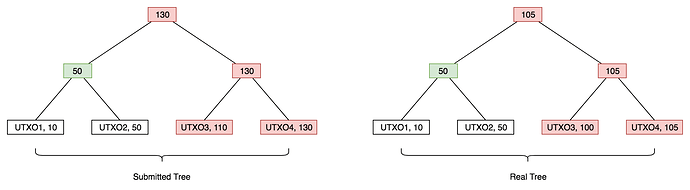
Let’s look at how this works:
Here, a user has submitted the tree on the left as their sum tree. The real UTXO set (1,2,3,4) and the root of the submitted tree are known to the public. Anyone can therefore generate the real tree (shown on the right) and detect any differences (marked red).
We have to actually figure out which tree is correct. Typically, this process will be performed in the context of the EVM, where data is relatively expensive. These trees might be committing to hundreds, if not thousands, of outputs, so it’s not feasible to publish the output set. Instead, we perform a binary search down the tree to discover the leftmost leaf node at which the trees disagree. This requires both parties play a challenge/response game logarithmic in the length of the bitfield.
Unfortunately, this is an expensive process and simplification of this check is an open research question. There might be a significantly more concise way to check that the sum of the given UTXOs is valid. Some zero-knowledge protocol might work here, provided the proof can be generated within a sufficiently short period of time and is small enough to fit on-chain.
Protocol
Now we’ll get into the actual protocol! We’re going to assume that there’s a mass exit coordinator willing to organize a mass exit on behalf of some users. How this coordinator talks to users and collects information is out of scope for this post, but needs to be researched. These same communication/coordination problems also apply to Plasma XT.
A coordinator begins the mass exit process by selecting a set of UTXOs to be withdrawn. The set is identified by a pointer to a specific UTXO aggregation (block number, aggregation ID) and an offset within that aggregation. If the offset is m, then the nth bit in the bitfield points to the m + nth UTXO in the aggregation.
Once the UTXO set is selected, the coordinator asks owners of UTXOs in that set for signatures asserting that the mass exit is valid and that the user wants their UTXO to be withdrawn. The coordinator will then generate a bitfield where a 1 at some position asserts that a signature was received for the UTXO in question.
Then, to start the mass exit on the root chain, the coordinator submits (along with a large bond):
- A pointer to the selected aggregation (block number, aggregation ID).
- An offset within the selected aggregation.
- A bitfield.
- A total sum of all the balances in the mass exit in the form of the root of a sum Merkle tree.
Challenges
Invalid Merkle Sum Tree Challenge
A mass exit can be challenged if the sum attached to the exit is invalid. This challenge takes the form of the proof game described above. Only one of the two trees can be correct. If the users have the same UTXO set but different summations, the contract can easily detect the correct tree. If the users iterate down the tree and find that the leftmost contested leaf contains a different UTXO (and therefore a different UTXO set), then one user must also provide a Merkle proof that the leaf was correctly included in the aggregation.
Failure by the challenger to respond at any step in the game ends the challenge. Failure by the coordinator to respond at any step in the game is considered a successful challenge. A successful challenge of this type blocks the entire exit.
Missing Signature Challenge
It’s possible for the coordinator to attempt to withdraw a UTXO without a user’s permission by placing a 1 in the bitfield for that UTXO. When the user detects that someone is attempting to exit their funds, they’ll submit a missing signature challenge. The coordinator must then respond (within some period of time) with the UTXO, a Merkle proof that the UTXO was included in the aggregation, and a signature from the owner of the UTXO.
Failure by the coordinator to respond to the challenge is considered a successful challenge. A successful challenge of this type blocks the entire exit.
Spent UTXO Challenge
A user can prove that a certain UTXO referenced in the mass exit is already spent by revealing the UTXO, a Merkle proof that the UTXO was included in the aggregation, and a signed spending transaction (also with proof). If the UTXO was spent before the mass exit was started (with a few blocks grace period), then the entire mass exit is blocked. If the UTXO was spent after the mass exit was started, then the sum is updated and the 1 in the bitfield is replaced with a 0.
Unfortunately, this type of challenge is problematic because the exit coordinator must front a lot of money to provide a bond big enough for each UTXO to be challenged as spent. It might be possible to mitigate this with a threshold number of challenges before the entire mass exit is simply blocked. This isn’t the most ideal mechanism and needs some work.
Priority
Mass exits have priority as if they were the last transaction in the block of the referenced UTXO aggregation. This ensures that mass exits of later
Finalization
When a mass exit is finalized, the sum value is transferred to another smart contract users can withdraw funds from this contract by referencing the bitfield and proving that they own some UTXO in the mass exit.
Concerns/Open Questions
There are currently several concerns about or potential areas of improvement for this design.
Mass Exit User Fee
Users should pay a fee for their mass exit. However, we want users to be able to generally pay less than they might if they submitted a single exit. The actual cost will likely depend on the relationship between the user and the coordinator. A wallet provider may choose to provide this service for “free” and recover their costs elsewhere.
Open questions:
- How much should it cost to join a mass exit?
- How should users actually pay to join the mass exit?
Mass Exit Bond Magnitude
The coordinator needs to front a lot of money to account for the cost of a (potential) spent UTXO challenge on every single UTXO in the mass exit. This relatively high capital lockup cost will limit the set of users who can actually become mass exit coordinators.
If we can be sure that the users in the mass exit have signed off on the exit (maybe with some sort of aggregate signature scheme), then we can make future spends a malicious act by the operator. This would also remove the need for a per-user missing signature challenge.
Open questions:
- Can we avoid an extremely large bond?
- Can the coordinator prove up-front that all of the owners in the mass exit have actually signed off?
Invalid Merkle Sum Tree Challenge Cost
A challenge that proves the sum tree to be invalid requires log(n) responses by each user (so a total of 2log(n) transactions). If we cap the number of UTXO in a mass exit at 8000, then that’s 26 total required transactions. Split evenly over a week, each user has about 6 hours to respond. Ethereum can be (and has been) spammed for this much time.
Open questions:
- Can we optimize the challenge/response game if users provide multiple tree levels at the same time?
- Can we come up with a better way to prove that the sum value of the leaves is valid?