We’d like to thank the teams from Polygon Zero, gnark project at Consensys, Pado Labs, and Delphinus Lab for their valuable review and feedback on this post.
The Pantheon of Zero Knowledge Proof
Over the past several months, we’ve dedicated a significant amount of time and effort into developing cutting-edge infrastructure that leverages zk-SNARK succinct proofs. As part of our development efforts, we have tested and used a wide variety of Zero-Knowledge-Proof (ZKP) development frameworks. While this journey has been rewarding, we do realize that the abundance of available ZKP frameworks often creates a challenge for new developers who are trying to find the best fit for their specific use cases and performance requirements. With this pain point in mind, we believe a community evaluation platform that is able to provide comprehensive benchmark results is needed and will greatly aid in the development of these new applications.
To fulfill this need, we are launching the Pantheon of Zero Knowledge Proof as a public good community initiative. The first step will be to encourage the community to share reproducible benchmarking results from various ZKP frameworks. Our ultimate goal is to collectively and collaboratively create and maintain a universally recognized evaluation testbed that covers low-level circuit development frameworks, high-level zkVMs and compilers, and even hardware acceleration providers. We hope that this initiative will expedite the adoption of ZKPs by facilitating informed decision-making, while also encouraging the evolution and iteration of the ZKP frameworks themselves by providing a set of commonly referenceable benchmarking results. We are committed to investing in this initiative and invite all like-minded community members to join us and contribute to this effort together!
A First Step: Benchmarking Circuit Frameworks using SHA-256
In this blog post, we take the first step towards building the Pantheon of ZKP by providing a reproducible set of benchmark results using SHA-256 across a range of low-level circuit development frameworks. While we acknowledge that other benchmarking granularities and primitives are possible, we selected SHA-256 due to its applicability to a wide range of ZKP use cases, including blockchain systems, digital signatures, zkDID and more. It’s also worth mentioning that we also leverage SHA-256 in our own system, so it is quite convenient for us as well! ![]()
Our benchmark evaluates the performance of SHA-256 on various zk-SNARK and zk-STARK circuit development frameworks. Through this comparison, we seek to provide developers with insights into the efficiency and practicality of each framework. Our goal is that these findings will enable developers to make informed decisions when selecting the most suitable framework for their projects.
Proving Systems
In recent years, we’ve observed a proliferation of zero-knowledge proving systems. While it is challenging to keep up with all of the exciting advances in the space, we’ve carefully selected the following proving systems based on their maturity and developer adoption. Our aim is to present a representative sample of different frontend/backend combinations.
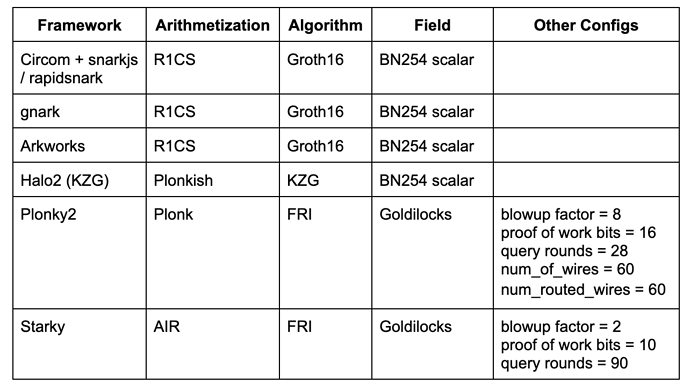
- Circom + snarkjs / rapidsnark: Circom is a popular DSL for writing circuits and generating R1CS constraints while snarkjs is able to generate Groth16 or Plonk proof for Circom. Rapidsnark is also a prover for Circom that generates Groth16 proof and is usually much faster than snarkjs due to the use of the ADX extension, which parallelizes proof generation as much as possible.
- gnark: gnark is a comprehensive Golang framework from Consensys that supports Groth16, Plonk, and many more advanced features.
- Arkworks: Arkworks is a comprehensive Rust framework for zk-SNARKs.
- Halo2 (KZG): Halo2 is Zcash’s zk-SNARK implementation with Plonk. It is equipped with the highly-flexible Plonkish arithmetization that supports many useful primitives, such as custom gates and lookup tables. We use a Halo2 fork with KZG support from the Ethereum Foundation and Scroll.
- Plonky2: Plonky2 is a SNARK implementation based on techniques from PLONK and FRI from Polygon Zero. Plonky2 uses a small Goldilocks field and supports efficient recursion. In our benchmarking, we targeted 100-bit conjectured security and used the parameters that yielded the best proving time for the benchmark job. Specifically, we used 28 Merkle queries, a blowup factor of 8, and a 16-bit proof-of-work grinding challenge. Moreover, we set num_of_wires = 60 and num_routed_wires = 60.
- Starky: Starky is a highly performant STARK framework from Polygon Zero. In our benchmarking, we targeted 100-bit conjectured security and used the parameters that yielded the best proving time. Specifically, we used 90 Merkle queries, a blowup factor of 2, and a 10-bit proof-of-work grinding challenge.
The table below summarizes the above frameworks with the relevant configurations used in our benchmarking. This list is by no means exhaustive and many state-of-the-art frameworks/techniques (e.g., Nova, GKR, Hyperplonk) are left for future work.
Please be aware that these benchmark results are only for circuit development frameworks. We plan to publish a separate blog benchmarking different zkVMs (e.g., Scroll, Polygon zkEVM, Consensys zkEVM, zkSync, Risc Zero, zkWasm) and IR compiler frameworks (e.g., Noir, zkLLVM) in the future.
Benchmark Methodology
To benchmark these various proving systems, we computed the SHA-256 hash for N bytes of data, where we experimented with N = 64, 128, …, 64K (with one exception being Starky, where the circuit repeats the SHA-256 computation for a fixed 64-byte input but maintains the same total number of message chunks). The benchmark code and SHA-256 circuit implementations can be found in this repository.
Furthermore, we conducted the benchmarking of each system using the following performance metrics:
- Proof Generation Time (including witness generation time)
- Peak Memory usage during proof generation
- Average CPU Utilization % during proof generation. (This metric reflects the degree of parallelization during proof generation)
Please note that we are making some “hand-waving” assumptions regarding the proof size and proof verification cost, as these aspects can be mitigated by composing with Groth16/KZG before going on-chain.
The Machines
We conducted our benchmarking on two different machines:
- Linux Server: 20 Cores @2.3 GHz, 384GB memory
- Macbook M1 Pro: 10 Cores @3.2Ghz, 16GB memory
The Linux server was used to simulate the scenario with many CPU cores and abundant memory. While the Macbook M1 Pro, which is commonly used for R&D, has a more powerful CPU with fewer cores.
We enabled multithreading where optional, but we did not utilize GPU acceleration in this benchmark. We plan to include GPU benchmarking as part of our future work.
Benchmark Results
Number of Constraints
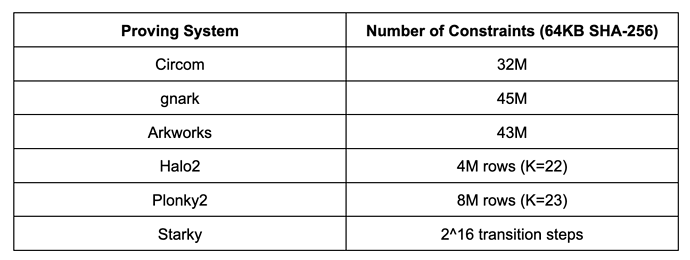
Before we move on to the detailed benchmarking results, it’s useful to first understand the complexity of the SHA-256 by looking at the number of constraints in each proving system. It is important to be aware that the constraint numbers in different arithmetization schemes are not directly comparable.
The results below correspond to a pre-image size of 64KB. While results may vary with other pre-image sizes, they can be roughly scaled linearly.
- Circom, gnark, and Arkworks all use the same R1CS arithmetization, and the number of R1CS constraints for computing 64KB SHA-256 is roughly 30M to 45M. The difference among Circom, gnark, and Arkworks is likely due to implementation differences.
- Halo2 and Plonky2 both use Plonkish arithmetization, where the number of rows range from 2^22 to 2^23. Halo2’s implementation of SHA-256 is much more efficient than that in Plonky2 due to the use of lookup tables.
- Starky uses AIR arithmetization where the execution trace tables require 2^16 transition steps.
Proof Generation Time
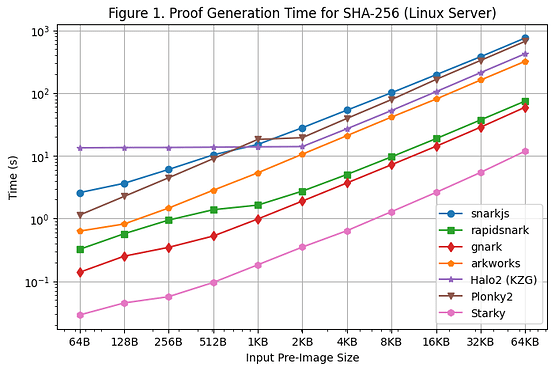
[Figure 1] illustrates the proof generation time of each framework for SHA-256 over the various pre-image sizes, using the Linux Server. We are able to make the following observations:
- For SHA-256, Groth16 frameworks (rapidsnark, gnark, and Arkworks) generate proofs faster than Plonk frameworks (Halo2 and Plonky2). This is because SHA-256 mainly consists of bitwise operations where wire values are either 0 or 1. For Groth16, this reduces most of the computations from elliptic curve scalar multiplication to elliptic curve point addition. However, wire values are not directly used in Plonk’s computations, so the special wire structure in SHA-256 does not reduce the amount of computation needed in Plonk frameworks.
- Among all of the Groth16 frameworks, gnark and rapidsnark are 5x-10x faster than Arkworks and snarkjs. This is thanks to their superior capability of utilizing multiple cores to parallelize proof generation. Gnark is 25% faster than rapidsnark.
- For the Plonk frameworks, Plonky2 is 50% slower than Halo2 for SHA-256 when using a larger pre-image size of >= 4KB. This is because Halo2’s implementation heavily utilizes a lookup table to speed up bitwise operations, resulting in 2x fewer rows than Plonky2. However, if we compare Plonky2 and Halo2 with the same number of rows (e.g., SHA-256 over 2KB in Halo2 vs. SHA-256 over 4KB in Plonky2), Plonky2 is 50% faster than Halo2. If we implement SHA-256 with a lookup table in Plonky2, we should expect Plonky2 to be faster than Halo2, although the Plonky2 proof size is larger.
- On the other hand, when the input pre-image size is small (<=512 bytes), Halo2 is slower than Plonky2 (and other frameworks) due to the fixed setup cost of the lookup table that accounts for the majority of the constraints. However, as the pre-image increases, Halo2’s performance becomes more competitive, with a proof generation time that remains constant for pre-image sizes up to 2KB and then scales almost linearly, as can be observed in the graph.
- As expected, Starky’s proof generation time is significantly shorter (5x-50x) than any SNARK framework, but this comes at the cost of a much larger proof size.
- An additional note is that even if the circuit size is linear in the size of the pre-image, the proof generation grows super-linearly for SNARKs due to the O(nlogn) FFT (although this is not obvious on the graph due to the log scale).
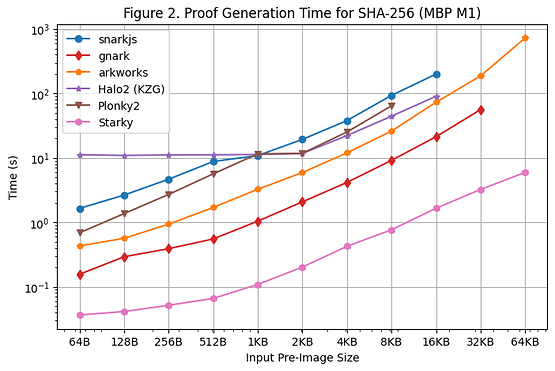
We also conducted a proof generation time benchmark on the Macbook M1 Pro, as illustrated in [Figure 2]. However, it is important to note that rapidsnark was not included in this benchmark due to its lack of support for arm64 architecture. In order to use snarkjs on arm64, we had to generate the witness using webassembly, which is slower than the C++ witness generation used on the Linux Server.
There were several additional observations when running the benchmark on Macbook M1 Pro:
- Except for Starky, all SNARK frameworks encountered out-of-memory (OOM) errors or used swap memory (resulting in slower proving time) when the pre-image size became large. Specifically, Groth16 frameworks (snarkjs, gnark, Arkworks) began to use swap memory when the pre-image size was greater than or equal to 8KB, and gnark encountered OOM for 64KB. Halo2 encountered a memory limit when the pre-image size was greater than or equal to 32KB. Plonky2 begins to use swap memory when pre-image size was greater than or equal to 8KB.
- FRI-based frameworks (Starky and Plonky2) were about 60% faster on the Macbook M1 Pro than on the Linux Server, while other frameworks saw similar proving times as compared to those on the Linux Server. As a result, Plonky2 achieved almost the same proving time as Halo2 on the Macbook M1 Pro, even though the lookup table was not used in Plonky2. The main reason for this is that the Macbook M1 Pro has a more powerful CPU but with fewer cores. FRI mainly conducts hash operations, which are more sensitive to CPU clock cycles but not as parallelizable as KZG/Groth16.
Peak Memory Usage
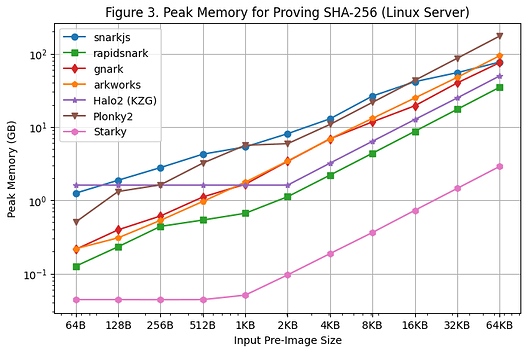
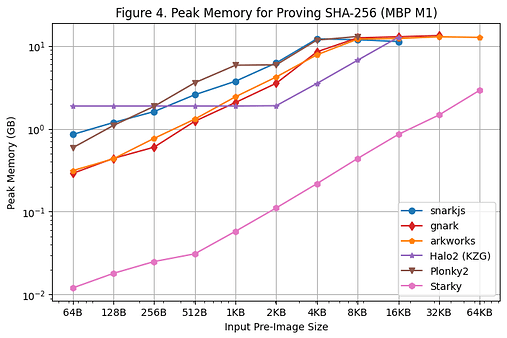
The peak memory usage during proof generation on the Linux Server and Macbook M1 Pro is shown in [Figure 3] and [Figure 4], respectively. The following observations can be made based on these benchmarking results:
- Among all of the SNARK frameworks, rapidsnark is the most memory efficient. We also see that Halo2 uses more memory when the pre-image size is smaller due to the fixed setup cost of the lookup table, but consumes less memory overall when the pre-image size is larger.
- Starky is more than 10x more memory efficient than SNARK frameworks. This is in part due to its use of fewer rows.
- It should be noted that the peak memory usage remains relatively flat on the Macbook M1 Pro as the pre-image size becomes large due to the usage of swap memory.
CPU Utilization
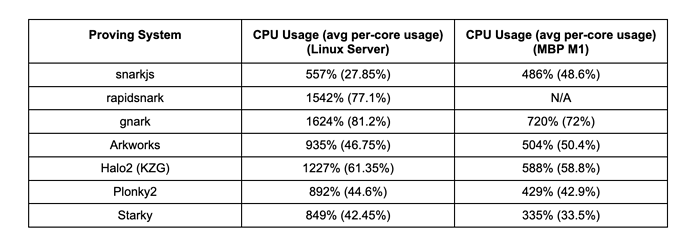
We evaluated the degree of parallelization for each proving system by measuring the average CPU utilization during proof generation for SHA-256 over a 4KB pre-image input.. The table below shows the average CPU utilization (and the average utilization per core in the parentheses) on both the Linux Server (with 20 cores) and the Macbook M1 Pro (with 10 cores).
The key observations are as follows:
- Gnark and rapidsnark show the highest CPU utilization on the Linux Server, indicating their ability to efficiently use multiple cores and parallelize proof generation. Halo2 also demonstrates good parallelization performance.
- Most frameworks demonstrate 2x CPU utilization on the Linux Server as compared to the Macbook Pro M1, the exception to this is snarkjs.
- Despite initial expectations that FRI-based frameworks (Plonky2 and Starky) might struggle to use multiple cores effectively, they perform no worse than some Groth16/KZG frameworks in our benchmarks. It remains to be seen if there will be any differences in CPU utilization on a machine with even more cores (e.g., 100 cores).
Conclusion and Future Work
This blog post presents a comprehensive comparison of the performance of SHA-256 on various zk-SNARK and zk-STARK development frameworks. Through the benchmark results, we’ve gained insights into the efficiency and practicality of each framework for developers who require succinct proofs for SHA-256 operations. Groth16 frameworks (e.g., rapidsnark, gnark) are found to be faster in generating proofs than Plonk frameworks (e.g., Halo2, Plonky2). The lookup table in Plonkish arithmetization significantly reduces the constraints and proving time for SHA-256 when using a larger pre-image size. Furthermore, gnark and rapidsnark demonstrate an excellent capability to utilize multiple cores for parallelization. Starky, on the other hand, shows a much shorter proof generation time but at the cost of a much larger proof size. In terms of memory efficiency, rapidsnark and Starky outperform other frameworks.
As the first steps to building the Pantheon of ZKP, we acknowledge that this benchmark result is far from being the final comprehensive testbed we aim for it to one day be. We welcome and are open to feedback and criticism and invite everyone to contribute to this initiative of making ZKP easier and more accessible for developers to use. We are also willing to provide grants for individual contributors to cover the costs of computational resources for large-scale benchmarking. Together, we can improve the efficiency and practicality of ZKP for the benefit of the wider community.