Binary trie format

[gballet]

Thanks to @sinamahmoodi for his input, @poemm and @carver for pointing out typos.

A method for the conversion of hexary tries into binary tries has been proposed in [1]. This proposal focuses on how the trie is represented, independently of the conversion method.
It is made up of three parts: the first part is a simpler write up, the second part illustrates the structure with an example, and the last part presents the formalization of the structure, using the notation from the yellow paper[2].

Overview

The proposed structure has only one type of node, which merges the functionalities of branch, extension and leaf nodes.

Field	Type	Description	Leaf node content	Internal node content
Prefix	RLP byte list	Prefix common to all subnodes of this node	bin prefix	bin prefix
Left	Hash / child RLP byte list	Pointer to the left child	empty RLP list	RLP of the left child, or its hash if it takes more than 32 bytes
Right	Hash / child RLP byte list	Pointer to the right child	empty RLP list	RLP of the right child, or its hash if it takes more than 32 bytes
Value	Bytes	Empty list if internal node, value bytes if leaf node.	value bytes	empty RLP list

In hexary tries, key encoding required a hex prefix to specify if the key length was odd or even, as well as specifying if the value was a leaf.
Likewise, key segments are encoded using a bin(ary) prefix. It packs all bits into the minimal number of bytes, and maintains a header to specifies how many bits of the last byte are in use. Bits are stored using the big endian notation. Unlike its hexary counterpart, the bin prefix doesn’t encode if the node is a leaf: this information is encoded by either child being empty.

Implementation

A first, naive implementation of this has been implemented in Geth[3]. It is based on the new snapshot feature introduced in Geth, in which all (key, values) are directly stored in the database.

Converting the trie from hexary to binary takes roughly 45 minutes on a mainnet machine, and the resulting dataset size is 20GB.

Example

Let’s assume a trie with the following three (key, value) pairs:

Binary key	Hexadecimal key	Hex value
1100 1010 1111 1110	cafe	00
1100 1010 1111 1111	caff	01
1011 1110 1110 1111	beef	02

First key

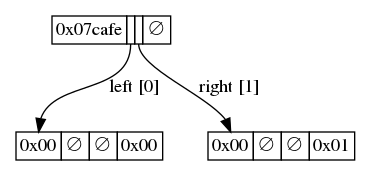
Upon insertion of the first key, the trie would look like:

There are 2 bytes in key 0xcafe, and all the nodes in the trie (i.e. only one) are prefixed by the same bit string (1100 1010 1111 1110, that is, the bits of 0xcafe). So the prefix of this single node is cafe.
Since all 8 bits are being used in the last byte, the value of the first byte in \mathtt{BP}(0xcafe) is 8 \mod 8 = 0.
This node has no children so both left and right child are empty values.

Second key

Inserting the second value will cause a fork at the last bit:

The last bit in the root is not used, so the first byte of the bin prefix is now 7, although the prefix seems not to have changed from its initial value (the last bit is to be set to 0, which is the value it already had).
Two sub-nodes had to be inserted, the left one to contain the initial value 0x00, and the second one to contain the new value 0x01. Neither of these nodes have a prefix since the fork occurs at the last bit, but their bin prefix is therefore simply 0x00, since all the bits in the non-existent last byte are being used.

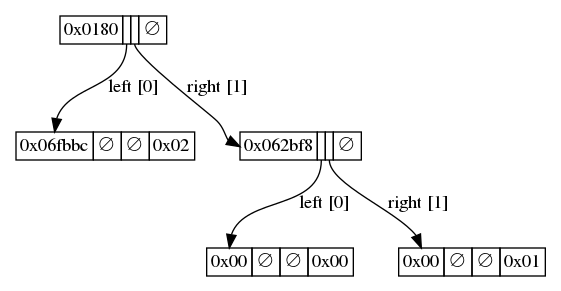
Third key

Inserting the third value will cause a fork at the second bit:

The root is now only 1 bit long, which is why the first byte of its bin prefix reflects is 1. That bit is 1, and it’s packed to the left so the byte key is 0b10000000 == 0x80.
The new leaf has 6 bits since the top bit is stored in the root’s bin prefix and the second bit 0 is covered by going left in the trie. The byte value are the remaining 0b11111011101111 part of the key, which have been packed to the left, so 0b1111101110111100 == 0xfbbc.
An intermediate node is also created on the c branch, and contains the former key prefix 0xcafe = 0b1100101011111110 whose first two bits have been removed, and the remaining packed to the left. So that’s 0b0010101111111000 == 0x2bf8.

Formalization

Notation

The notation here is based on that of the yellow paper.

In the formulas of this text, the product symbol \prod is redefined to mean the element concatenation, formally:

\forall a=(a_0,a1,...,a_{n-1}), \forall (i,j) : 0 \le i \le j \lt n, \prod_{i}^{j}a_i \equiv (a_i, a_{i+1}, ..., a_{j-1}, a_j)

It is also assumed that bit strings are indefinitely extensible with 0s to the right. Formally:

\forall x : x \in \{0,1\}^n, \forall i : i \in \mathbb{N}, i \ge \lVert x \rVert \implies x[i] = 0

Binary prefix

A trie node encode a segment of its key with the help of a Binary Prefix, which is a function that is used to pack the bits of a key into a sequence of bytes.

Formally, the binary prefix function \mathtt{BP} is defined as:

\mathtt{BP}(x) : x \in \{0,1\}^n \equiv \Big(\lVert x \rVert \mod 8,\prod_{i=0}^{\lceil \lVert x \rVert \div 8 \rceil}\sum_{k=8i}^{8i+7}{\big(x[k]\times2^{k-8i}}\big)\Big)

which means that for a sequence of bits b_0, b_1, ..., b_n, \mathtt{BP} will return a sequence of bytes in which the first byte will contain the number of bits used in the last byte, and then a sequence of bytes in which all b_i bits are packed.

Binary Trie

Equations (190) and (191) in the yellow paper are updated to reflect that keys are viewed as a series of bits (as opposed to nibbles), and the notation is still big-endian:

b(\mathfrak{I}) = \{ (\mathbf{k}_0' \in \{0, 1\}^n, \mathbf{v}_0 \in \mathbb{B}), (\mathbf{k}_1' \in \{0, 1\}^n, \mathbf{v}_1 \in \mathbb{B}), ... \} \\ \forall n : \quad \forall i < 8\lVert\mathbf{k}_{n}\rVert: \quad \mathbf{k}_n'[i] \equiv \mathbf{k}[i \div 8]_{(i \mod 8)}

The \mathtt{TRIE} function is still defined as:

\texttt{TRIE}(\mathfrak{I}) \equiv \texttt{KEC}(c(\mathfrak{I}, 0))

and accordingly the trie’s node cap function is still defined as:

n(\mathfrak{I},i)\equiv\begin{cases} () & \text{if} \quad \mathfrak{I}=\varnothing \\ c(\mathfrak{I},i) & \text{if} \quad \lVert c(\mathfrak{I}, i) \rVert < 32 \\ \texttt{KEC}(c(\mathfrak{I}, i)) & \text{otherwise} \end{cases}

Only one type of node exists, which contains 4 items:

• A key prefix, which is the part of the key common between all sub-nodes of this node;
• A left (respectively, right) pointer that is pointing to the root of the left (respectively, right) subtree; and
• a value field that contains the arbitrarily long value stored at this node.

A leaf is a node with an empty left and right child. Note that a node either has two non-empty children, or both of them are empty.

Consequently the structural composition function (194) is updated to:

c(\mathfrak{I}, i) \equiv \texttt{RLP}(\texttt{BP}(I_0[i..(j-1)]), u(0), u(1), v) \quad \text{where} \begin{array}[t]{rcl} j & = & \max \{ x : \exists \mathbf{l}: \lVert \mathbf{l} \rVert = x \wedge \forall I \in \mathfrak{I}: I_0[0 .. (x - 1)] = \mathbf{l} \} \\ u(k) & \equiv & n(\{I : \mathfrak{I} \wedge I_0[i]=k\}, j+1) \\ v & = & \begin{cases} I_1 & \text{if} \quad \exists I : I \in \mathfrak{I} \wedge \lVert I_0 \rVert = i \\ () & \text{otherwise} \end{cases} \end{array}

References

1. hex -> bin conversion with the overlay tree method
2. The ethereum yellow paper
3. Binary trie test implementation

[vbuterin]

Thanks for the ongoing hard work!

1. Do we necessarily want to merge all types of node into one? A realistic Merkle path going into the state in most cases would look like a series of branch nodes followed by an extension with a leaf, so the efficient thing to do seems like it would be to have a single-bit flag that says “is this a branch or an extension node”, and then you would have clean two-child nodes: either (left, right) or (extension, child). We could even establish the convention that an extension node with an empty extension is a leaf node.
2. The above would also make it easier to have a clean rule that says “a tree node is 64 bytes”, which seems valuable, especially in the context of the more general trend to move away from RLP and toward 32-byte-chunk alignment.
3. Do we need the functionality of the tree telling us where the leaves are? I suppose the alternative would be a fixed-total-depth tree, which could simplify things.
4. Has there been much thinking about reforming the current two-layer trie structure into a single-layer trie? If so, how would that fit in here? Or are you modeling those two issues as completely separate?

[gballet]

Thanks for the feedback! The goal of having only one type of node is to reduce the amount of DB reads since IO is a bottleneck in clients, and also save the extra 32 bytes for the pointer to the extension’s child.

1&2: Getting rid of RLP is a laudable goal, let’s go for it!

I’m trying to reconcile how on one side we could use the first bit to tell the ext from the branches, and keep the 64 bits alignment on the other? Both left and right pointers take each 32 bytes out of 64.
I see three possibilities for a fix, none of which I am really enthusiastic about:

• only use 31 bits out of the left pointer’s 32;
• keep a separate tree for the bitmap;
• have a 96 byte key following the same ext-in-branch model as initially proposed.

The latter would be an optimization working better towards the bottom of the trie, where most of the extension nodes are to be found. Also, 3 bits would be missing because of the \mathtt{BP}() field.
I’m going to test both approaches on a full sync, to see if this approach really has a positive speed/size impact.

3&4: The intent is to be flexible w.r.t the key sizes, and therefore not to enforce a fixed total-depth in order to support both 20 byte and 32 byte addresses. I suggested encoding a leaf as a node with two null children for this reason.

In the model you suggest, we could indeed either encode a leaf as an ext node with an empty prefix, or as a branch node with a null left branch and the value stored in the right branch. The difference would be only one bit.

So in both cases, it is possible to determine if a key is a leaf from its encoding and not require an explicit termination marker. I don’t feel forcing a fixed-total-depth tree would simplify things enough to make up for its loss of flexibility.

[pipermerriam]

@gballet

1&2: Getting rid of RLP is a laudable goal, let’s go for it!

I’m on a spec that removes RLP

Overall this looks great. It sounds like you have a working implementation in Geth. Would it be valuable for you to have someone else work up an independent implementation to compare notes?

[vbuterin]

The goal of having only one type of node is to reduce the amount of DB reads since IO is a bottleneck in clients, and also save the extra 32 bytes for the pointer to the extension’s child.

Another possible option is a compromise similar to what I suggested in Optimizing sparse Merkle trees, where from a hashing point of view the structure can be represented as a binary hash tree, but in the database it would be a different structure. That is, we define hash_tree_node(node) as follows:

1. Let tree_node = (prefix, left, right, value)
2. If prefix is empty, return hash(0, value) if there’s a value, otherwise hash(left, right)
3. If prefix is nonempty, return hash(prefix, hash_tree_node(EMPTY_PREFIX, left, right, value))

At the DB level, I imagine you would be compressing many of these nodes together anyway, so further differences between hash structure and storage structure don’t really matter much.

This relies on the assumption that (i) 0 represents the empty prefix, and (ii) nonempty prefixes are distinguishable from valid hash outputs.

There is a bit of efficiency decrease in hashing, but it’s a negligible amount because as I mentioned, typically only the bottom leaf in the tree is an extension node, whereas the O(log(n)) ~= 28 nodes in the middle are not.

I think my desire to have the entire tree be navigable as a binary hash tree comes from (i) desire to be compatible with eth2’s SSZ frameworks, and (ii) desire to be easily compatible with future ZKP frameworks, which work more easily if hashes can be assumed to be in the “two 32-byte chunks -> one 32-byte chunk” format. Though if there’s better ways to achieve those goals I’m happy to listen; I’m not at all convinced that the specific thing I wrote above is optimal.

[poemm]

It seems that everyone agrees to use binary radix trees. We just haven’t decided on a merkleization rule.

Here is @gballet 's merkleization rule (loosely), ignoring RLP which I oppose keeping.

M1.
internal_node_hash = hash( prefix_length || prefix_length%8 || prefix_bits || left_child_hash || right_child_hash )
leaf_hash = hash( prefix_length || prefix_length%8 || prefix_bits || leaf_value )

And here is @vbuterin 's merkleization rule (loosely).

M2.
if prefix is empty:
internal_node_hash = hash( left_child_hash || right_child_hash )
leaf_hash = hash( 0 || leaf_value )
if prefix is non-empty:
internal_node_hash = hash( prefix_bits || hash( left_child_hash || right_child_hash ))
leaf_hash = hash( prefix_bits || hash( 0 || leaf_value ) )

(For M2, distinguishing between empty prefixes, nonempty prefixes, and hash outputs remains a problem.)

I propose that we explore dropping prefix bits from merkleization. They are awkward, require bit-twiddling, and add witness overhead. Here is a third proposed merkleization rule.

M3.
internal_node_hash = hash( left_child_hash || right_child_hash || prefix_length)
leaf_hash = hash( leaf_key || hash( leaf_value ) || prefix_length )

Note that we dropped prefix_bits, but added leaf_key which is cryptographically related to prefix_bits. And because prefix_length is usually 0x00, this merkleization rule usually meets @vbuterin 's goal of “two 32-byte chunks -> one 32-byte chunk” format. We also hash leaf_value because it is greater than 32-bytes for account data. Rule M3 makes proofs-of-exclusion include a neighboring leaf, but this overhead may be smaller than the overhead of including prefix_bits in the witness, not to speak of the awkwardness of including prefix_bits.

I am not sure which merkleization rule is best for statelessness.

[vbuterin]

By dropping extension bits you basically mean allowing “extension nodes” only at leaf level? I’ve definitely proposed such a simplification before. The main criticism though is that we also want to simplify the trie by converting it from a 2-level structure (accounts, then code/storage) into a 1-level structure. And in such a 1-level structure, distinct objects that are part of the same account would share the first half of their trie key but not the second. If there are no intermediate extension nodes, a Merkle branch to such a cluster would require 256 branching nodes. Any idea how to better deal with this situation?

[poemm]

To clarify, M3 keeps all extensions (“prefixes”, “edge labels”). But for merkleization, just includes the extension length (“prefix length”, “edge label length”). My post was confusing because it used “extension bits” and “prefix bits” interchangeably, now edited to consistently use “prefix bits” (although we should use “edge labels” since we are discussing radix trees).

I agree with everything you wrote.

[carver]

Both children always present?

@gballet

Note that a node either has two non-empty children, or both of them are empty.

What about a tree storing values at key=0xab and key=0xabcd? I imagine it having a node at the 0xab prefix with a value attached. It would have a right child (because 0xc is 0b1100, with the first bit being 1), but not a left child. Especially since you mentioned:

@gballet

The intent is to be flexible w.r.t the key sizes, and therefore not to enforce a fixed total-depth in order to support both 20 byte and 32 byte addresses.

Disallowing keys that are prefixes of others

Several of the hashing schemes above seem to assume that no key can be a prefix of another key. That would disallow of some of the most obvious ways to combine the state trie into a single trie.

It would still be possible to combine the trie I expect, but require a little refactoring. Something like:

• Account balance & nonce stored at key = hash(address) + 0x00
• Each storage value stored at key = hash(address) + 0x02 + hash(storage_slot)
• Merkelized bytecode at key = hash(address) + 0x03 + ... TBD

It does come with costs:

• It is a bit messier to answer the question “does this account exist?”
• It would compel trie implementations to implement a “delete range” API in order to erase all of an account at once
• Ugly 33 and 65 byte keys

Most of those costs are implicit in combining into a single trie though. Really the only change is adding the 0x00 byte at the end of the account balance and nonce info, so it’s not a prefix of the others.

I don’t have enough background about the mentioned goal of supporting both 20 byte and 32 byte addresses, though, to tell if we can avoid one key ever being a prefix another.

Encoding leaves with null bytes for left & right children

@gballet

Unlike its hexary counterpart, the bin prefix doesn’t encode if the node is a leaf: this information is encoded by either child being empty.

I like simplicity of a predictable element count, but adding two “null” bytes to the final serialized node isn’t a tradeoff I would make for that simplicity. With the state trie in the rough range of 100 Megaleaves to 1 Gigaleaf, that can have a meaningful impact on sync time.

It looks like we could use 2 of those 5 top bits in the bin prefix to flag that the left or right child as null, then just skip it in the node body.

Misc

There appears to be a bit-flip typo in the first f in caff:

@gballet

Let’s assume a trie with the following three (key, value) pairs:

Binary key	Hexadecimal key	Hex value
1100 1010 1111 1110	cafe	00
1100 1010 1110 1111	caff	01
1011 1110 1110 1111	beef	02

I expected:

Binary key	Hexadecimal key	Hex value
1100 1010 1111 1110	cafe	00
1100 1010 1111 1111	caff	01
1011 1110 1110 1111	beef	02

[vbuterin]

It would compel trie implementations to implement a “delete range” API in order to erase all of an account at once

BTW removing the need to do this is (a big part of) exactly why @AlexeyAkhunov has been pushing to get rid of the SELFDESTRUCT opcode.

[gballet]

Thanks for your feedback.

@carver

What about a tree storing values at key= 0xab and key= 0xabcd ? I imagine it having a node at the 0xab prefix with a value attached. It would have a right child (because 0xc is 0b1100 , with the first bit being 1 )

You are considering storage trees “hanging” from account nodes (like in @AlexeyAkhunov’s approach). I had a different model in mind. You are right, though, “hanging” storage is the correct model. This proposal still works in that case, as internal nodes also have a value. It’s just that the “either 2 children or none” property doesn’t hold anymore.

@carver

It looks like we could use 2 of those 5 top bits in the bin prefix to flag that the left or right child as null, then just skip it in the node body.

Exactly, and a third one to flag the presence of a value as well.

@carver

Merkelized bytecode at key = hash(address) + 0x03 + ... TBD

Code Merkelization isn’t an issue in this case: this is for the internal account+storage state, not proof generation.

[gballet]

@poemm

M1.

For clarity, the rule is this:
node_hash = hash(prefix_length%8 || prefix_bits || left_child_hash || right_child_hash || value)

@poemm

M3.

I like this because it is pretty much the multiproof approach, and one can use a flat DB model. Then keys can be stored sequentially and the key length eventually doesn’t matter.

Practically, though, things get a bit more complicated: For example, when doing an insert, one needs to “guess” what the neighboring values are because bits aren’t stored along the path to get there.
It can be done, and I can think of a few hacks in the case of geth. I am not yet convinced it can be done by every client, though.

I am currently running tests on the “M2” approach to see how much the performance and size are impacted, so that I can then compare how much of a gain M3 is, I’m curious.

[poemm]

@gballet

Practically, though, things get a bit more complicated: For example, when doing an insert, one needs to “guess” what the neighboring values are because bits aren’t stored along the path to get there.

Your current implementation should work for M1, M2, and M3, you just hash differently. For example M3 omits prefix_bits when hashing. You are correct that M3 hashing include leaf_key at each leaf, but witnesses must have access to that anyway.

I’m not sure which merkleization rule is best.

[vbuterin]

Is there anything wrong with banning keys from being prefixes of other keys? I don’t think we need that possibility for a tree model; eg. I was thinking:

• address + 0x00 for balance
• address + 0x01 for nonce
• address + 0x02 + chunk_id for code
• address + 0x03 + storage_key for storage.

[carver]

@vbuterin

I was thinking:

• address + 0x00 for balance
• address + 0x01 for nonce
• address + 0x02 + chunk_id for code
• address + 0x03 + storage_key for storage.

jinx – I’m still thinking through the storage size implications, but it’s cool that we could get rid of encoding the account with rlp. You can see the ghost of the idea in how I skipped 0x01 here:

@carver

• Account balance & nonce stored at key = hash(address) + 0x00
• Each storage value stored at key = hash(address) + 0x02 + hash(storage_slot)
• Merkelized bytecode at key = hash(address) + 0x03 + ... TBD

[carver]

@gballet

@carver

Merkelized bytecode at key = hash(address) + 0x03 + ... TBD

Code Merkelization isn’t an issue in this case: this is for the internal account+storage state, not proof generation.

Ah, I meant if code merkelization gets internalized into the account trie before/during this proposal. Otherwise, it would be something like:

Full bytecode at key = hash(address) + 0x03

[ajlopez]

Well, I think that you don’t need to hash the storage slot, in this case. Anyway, I discourage the use of a nested storage slot after account key: storage is better to be considered as a separate concern, and this way, even allow to share same keys and values between storages of different accounts. Having the storage slot nested inside the account address key, implies, someway, that updating n storage slots after block execution, implies to create MORE intermediate nodes to update the trie, than in the current implementation, where the storage trie has less number of levels.

BTW I support that keys could be prefixes of other keys. IE in a storage trie, without hashing keys, we could save values under keys 0x01, 0x0101, 0x010101 and so on, removing the initial zeroes in many cases. The only remaining use for hashed keys for storage are the mappings in Solidity

[gballet]

Quikc update: I have run M1, M2 and M3 on mainnet (account trie only).

Type	Time	Size
M1	43min	13G
M2	42min	12G
M3	45min	13G

I’m waiting for one PR to be merged before doing the same thing with the storage tries.

Prototype code:

• M1 branch https://github.com/gballet/go-ethereum/tree/binary-tree-m1
• M2 branch https://github.com/gballet/go-ethereum/tree/binary-tree-m2
• M3 branch https://github.com/gballet/go-ethereum/tree/binary-tree-m3

[AlexeyAkhunov]

@gballet

Practically, though, things get a bit more complicated: For example, when doing an insert, one needs to “guess” what the neighboring values are because bits aren’t stored along the path to get there.
It can be done, and I can think of a few hacks in the case of geth. I am not yet convinced it can be done by every client, though.

Sorry, I am a bit late to the party, it took me a long time to get some fragments of time to understand what is going on. I find something like M3 variant proposed @poemm close to ideal. I do not really understand the concern with “guessing” what the neighbouring values are. As the implementer, you are free to chose which data structure you need for this. For example, we would be implementing this without needing any trees and inserts (we use approach based on the “prefix groups” and streaming computation of the state root). But if you are using trees, then why can’t this tree give you the information about the neighbouring values if you need it?

[gballet]

During our last conversation, @AlexeyAkhunov pointed out that removing the concept of extension nodes was addressing all the issues that I had with M2/M3. The structure becomes much simpler:

M4

node_hash = hash(left_child_hash || right_child_hash)
leaf_hash = hash(0 || leaf_value)

Pointing out of the most radical changes from M2/M3:

• There are no extension nodes in the merkelization rule
• The key value is encoded through the tree structure
• There is no more need for extracting key bits

Clients and witnesses are still welcome to use extension nodes and explicit keys to store their data.

For example, and in order to save space, a client can store the data using extension nodes. Single-child internal nodes are generated on the fly while merkelizing the stored extension node.