Authors: @Mikerah Afonso @sarisht
Shoutout to Gabearro Ventalitan Nerla Yun Qi and Surya for all the vibes and discussions!
This project was done as a Hackathon Project at IC3 camp last week.
TL;DR
We present a formal model or block building in blockchains. We show that block building is at least a combination of the Knapsack problem and the Maximum Independent Set problem, thus showing that block building is an NP-hard problem. Next, we provide various greedy algorithms with different tradeoffs. Then, we show simulation results to justify the algorithms and benchmarks. Our results show that tweaking the greedy solution with the results of the known knapsack constraint outperforms the currently used greedy algorithm by ~15% in terms of fee earned. Finally, we discuss how this is relevant for block builders in Ethereum in practice and directions for future research.
Introduction
Block building in Ethereum has evolved into a multimillion-dollar industry, particularly with the introduction of MEV-Boost. This has significantly increased the revenue earned by the builders. However, the builders’ algorithm for selecting transactions and transaction bundles needs more study. In collaboration with Flashbots, Mikerah (group lead for the project) has recently worked on a project that formalizes the model for block building as a knapsack problem. This model considers each transaction’s utility (the fee offered by the transaction) and cost (the gas used by the transaction), with a budget for the maximum price that can be paid (the gas limit for the block). The practical relevance of this research is evident, as it addresses a significant limitation of the current model, where not all transactions are independent of each other.
The Problem
Let’s delve into the heart of the matter by examining why transactions are not independent, a key challenge in block building.
Bitcoin Blockchain
The most critical problem described in the Satoshi Nakamoto blockchain paper was catching double-spending. If two transactions try to spend the same UTXO, only one of them should make it on-chain. Thus, we can see that some transactions are dependent on each other. However, that is not all; some transactions that interact with Bitcoin’s OP-Code design can also depend on each other. A classic example of this would be that in an HTLC, either a refund transaction (released by revealing a pre-image of a hash) or payment (released when the timelock on the transaction expires) can go through. If both transactions are simultaneously in the mempool, then the transactions conflict with each other.
Ethereum Blockchain
Ethereum inherits the double-spending transaction problem, but owing to its smart contract and gas fee design, it only partially suffers from the other type of conflict since the fee is paid based on the gas used. This causes the model to shift slightly, where the fee paid and the gas used depends on other chain transactions. Further, in the presence of searchers, some transactions are bundled such that multiple bundles contain the same transaction and thus cannot be included in the block simultaneously.
Model
We first introduce the assumptions we make before describing the mathematical formulations.
Assumptions
- Dependent fees and gas are hard to model since we cannot have a boolean representation. Thus, we only consider “Conflicts” and touch upon “Dependency.” Conflicts are situations in which the transactions cannot occur together, and dependency is when one transaction requires another transaction to be executed before it is valid.
- We further ignore the optimal ordering of transactions inside a block. Ordering transactions in a particular order can lead to higher profits due to MEV, which we ignore for the same reason as above.
- For Ethereum, under the conditions of EIP 1559, the fee considered is the part above the base fee. Any transaction with a negative fee is ignored.
Given these assumptions, we now model the binary allocation problem with constraints and dependencies as follows:
Let T be the set of transactions. A transaction in T is denoted by tx_i.
Let f_i denote the fee associated with a transaction tx_i.
Let g_i denote the gas associated with a transaction t_i
Let B be the maximum block gas limit.
Then, we have the following optimization problem
Maximise
Subject to
where,
- C_{ij} = 1 if t_i and t_j are conflicting transactions, 2 otherwise
- M_{ij} = 0 if t_j depends on t_i and can only be allocated after t_i, 1 otherwise
Since, in practice, it is hard for a block builder to infer the 3rd condition (without executing all of the transactions) within a limit snapshot of the transactions within their order flow pools, we can omit the 3rd constraint to simplify the problem. If the builder comes across such a transaction, it would be considered invalid.
As such, we can obtain the following simplified optimization problem
Maximise
Subject to
where,
- C_{ij} = 1 if t_i and t_j are conflicting transactions, 2 otherwise
Reductions
Now, we present formal arguments as to why block building is an instance of the knapsack problem and the maximum independent set problem.
Reduction to knapsack
The reduction of the above problem to knapsack is easy to see. We assume no conflicts arise amongst any transactions. In that case, the problem is the same as solving a knapsack problem, with the utility as the fee paid by the transaction, space occupied as the gas used by a transaction, and finally, the block’s gas limit determines the knapsack size. Thus, the block-building problem is at least as hard as the knapsack problem.
Reduction to Maximum Independent Set
If we can solve the above instance of block building problem without any constraint that limits the size of the block in polynomials, then consider the following instance where the block gas limit is set to the sum of gas of all transactions in the mempool. This would imply enough space for all the transactions in the mempool to fit in the block. This problem is now equivalent to finding the maximum weighted independent set because we can consider all transactions as vertices, and an edge exists between two vertices if the corresponding transactions conflict. The above reduction creates the instantiation of the maximum weighted independent set problem, which is again known as NP-hard.
Algorithms for approximate result
As we mentioned above, block building is an NP-hard problem with reductions to both the knapsack problem and the maximum weighted independent set problem. Since we know that the maximum weighted independent set problem doesn’t have a C-approximation, this implies that the block-building problem also doesn’t have a C-approximation.
As such, we devise several greedy algorithms in order to solve the block-building problem in practice.
Greedy Classic (GC)
We expect today’s builders to use the first algorithm we present. It follows the most widely used knapsack greedy solution, where all objects are sorted according to the ratio of their utility to cost, and then greedily allocate space to each object until you can no longer allocate more space. Due to the added conflict constraint, the builder must check for conflict with any transaction already added to the block. Thus, the algorithm works as follows:
Algorithm input: T = \{t_i\}, F = \{f_i\}, G = \{g_i\}
Algorithm output: An ordered block with gas used less than BL
Algorithm description:
Sort T by corresponding F/G
Let B := {}
Let BS := 0
For each t in T, f in F, g in G do:
if t has any conflict with tx in B: continue;
if g + BS < BL: B.append(t); BS += g
return B
In practice, the conflict between transactions is only known if simulated sequentially. We propose two constraints on how this conflict can be modeled.
- Two transactions t_1 and t_2 conflict if the transactions cannot be executed together. This can happen if some address is trying to double-spend some money it has or if two searcher bundles try to extract MEV from the transaction. We call this conflict a “Real” conflict.
- Two transactions t_1 and t_2 conflict if they interact with the same address. We call this conflict an “All” condition. These transactions do not necessarily invalidate each other. Still, we keep this as a potential conflict condition since this conflict is more straightforward to determine (constant size operation) than the other constraint (gas size operation), and thus can be helpful for builders optimizing based on the time computing is used.
Note: In the solution simulation, we assume that p=0.95 of transactions in the “All” conflict are not in the “Real” conflict.
Based on the definition of conflicts, we present the two baseline greedy solutions, which we label CG All and CG Real.
Knapsack Greedy
The greedy solution described above is not a good approximation solution. Looking back at the knapsack problem, we get a 1/2 approximation over the optimal solution by comparing the above classic greedy with the utility of the first object that was not allocated.
The algorithm begins by running an instance of the greedy classic. It then finds the highest paying (highest f/g) transaction and adds it to the block. Adding this transaction would require modification of the block since some transactions in block (B) conflicted with this transaction, or the transaction could not be inserted due to insufficient space. Thus, we remove transactions that conflict with this new addition and then make enough space to add this transaction. After inserting the transaction, we repeat the greedy insertion until the block is again full. We repeat the above algorithm until we have seen each transaction at least once over the greedy solution.
The pseudocode for the solution is as follows:
Sort T by corresponding F/G
Let B := {}
Let B_f:= {}
Let S := {}
Let BS := 0
while S != T:
let t := t in T, not in S, with maximum f/g:
remove any transaction from B that conflicts with t.
remove smallest f/g txs until there is space to insert t.
B.append(t)
S.append(t)
For each t in T, f in F, g in G do:
if t has any conflict with tx in B: continue;
if g + BS < BL: B.append(t); BS += g; S.append(t)
if sum(B.f) > sum(B_f.f): B_f = B
return B_f
# B.f is the fee corresponding to each transaction in B
In this greedy protocol, we attempt to enforce the inclusion of a transaction every time. It is still distinct from the greedy knapsack 1/2 approximation, but it tries to replicate what was accomplished by the knapsack greedy but for all items not picked by the greedy algorithm.
This solution will outperform its classic greedy counterpart since it computes maximum over all solutions, one of which is the classic greedy solution. Like the classic greedy solution, we analyze this when conflicts are “Real” and “All”.
Classic Greedy Informed Solutions
Solving the knapsack problem is very easy compared to all known NP-Hard problems, especially the maximum independent set condition we have been imposing. Thus, we allow the builder to solve the knapsack reasonably accurately and quickly via a BLP solver. The knapsack solution gives the builder some idea about how to build the block, and then when there are conflicting transactions in the chosen block, the “later” transactions are discarded. In this solution, we run a knapsack LP solution. On the output of the LP, we sort the output based on i) f/g ratio ii) f, and finally iii) g. The way greedy works here is that the transactions are picked in the order of the metric, and whenever there is a conflict, the LP solver is recalled, but removing constraints on the already added and the conflicting transaction (x_i is set to 1 for all that have already been chosen and x_i is set to 0 for the conflicting transaction). This is repeated until the block is full.
Let B := {}
Let B_c:= {nil}
Let BS := 0
Let C := {}
while B_c != B:
B_c = LP.solve(sum(x.f), x.g <= BL, C)
Sort B_c by "heuristic"
for t in B_c:
if t has any conflict with tx in B:
C.add(x_t = 0)
break;
B.append(t)
C.add(x_t = 1)
return B
# Replace "heurestic" by f/g for standard,
f for high-value
# Sorting is in descending order
We label these transactions as CGI-f/g and CGI-f. We only analyze the “All” conflicts for this since the time to run the algorithm is potentially higher than for the other Greedy Algorithms.
Simulation
Due to our limited time to work on the project, we tried to replicate the transaction data synthetically instead of working with real transactions. To properly simulate Ethereum mempool transactions, we choose the following dataset:
Dataset
We choose 2000 transactions under this distribution.
- 80%: SMALL: g ~ N(24k, 3k) f/g ~ N(16,4) - These low gas-consuming transactions have minimal smart contract interactions and thus use less gas. In almost all cases, the gas fees for these transactions are small since they are usually never a priority transaction.
- 18% : LARGE1: g ~ N(200k, 20K) f/g ~ N(16,4) - These represent transactions that have a significant contract execution; however, in this case, these are still not priority transactions, since the user is okay to wait for some time for the contract execution.
- 2% : LARGE2: g ~ N(200k, 20K) f/g ~ N(40,10) - These are the priority transactions. Usually, these have high gas usage since they mostly interact with, for example, DeFi contracts and want to be executed as soon as possible.
We simulate the conflicts among these transactions by randomly choosing transactions such that each transaction has a \sigma number of conflicts. While our preliminary results constitute the same \sigma across all types of transactions, in practice, the larger transactions, especially the high-paying ones, would have a more significant number of conflicts since usually MEV extracting bundles would be constructed around them.
Results
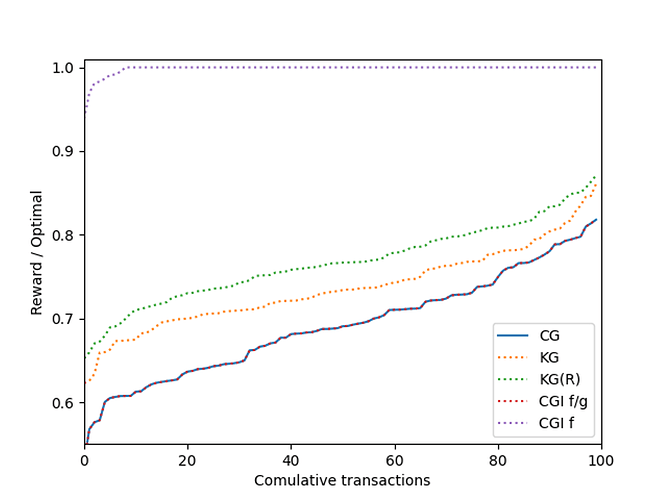
We ran our simulation over 100 blocks with the mempool created as above.
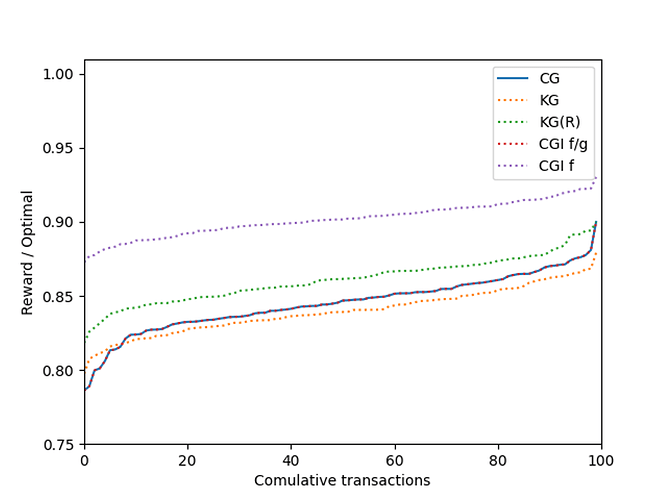
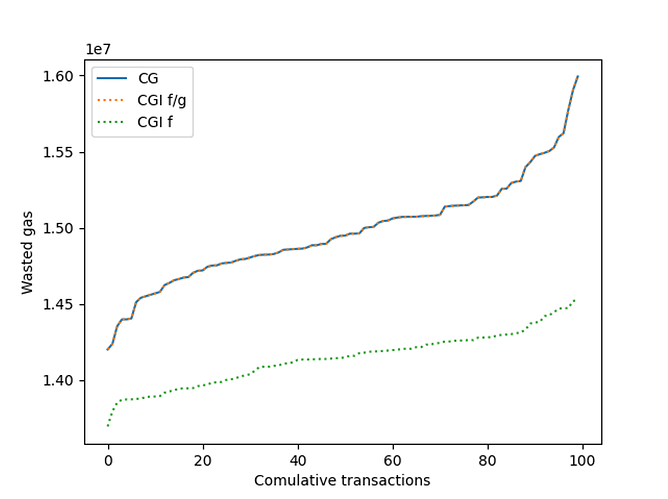
When we consider \sigma=2 number of conflicts per transaction, we see the following results:
Increasing the number of conflicts each transaction had increases the problem’s difficulty. Therefore, the various greedy algorithms have a larger separation in performance:
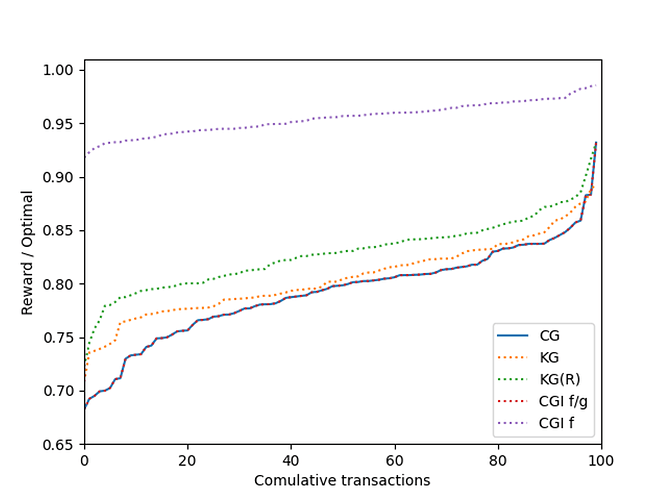
For \sigma = 10,
For \sigma = 20,
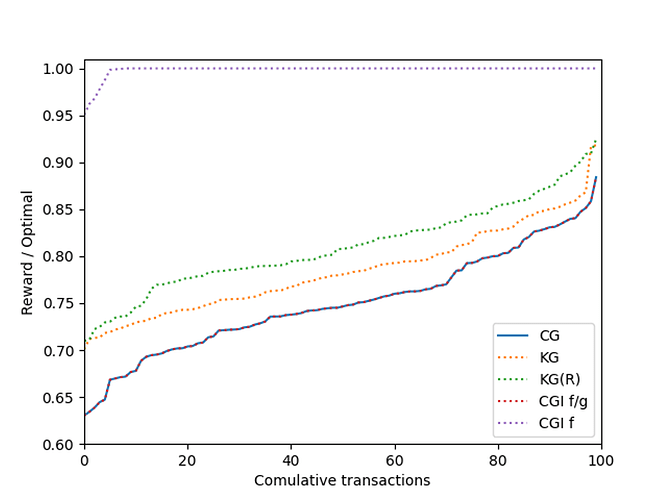
For \sigma = 40,
Future Research Direction
Based on our results, solving the block-building problem is an NP-Hard problem, and as long as conflicts exist amongst the transactions, it remains a complex problem.
However, this does not mean that all hope is lost. The block-building problem may have more potential than the Maximum Independent Set problem. Combining the space of Knapsack and Maximum Independent Set gives us a smaller search space to find a satisfactory approximate solution for the issue at hand.
Further, for Ethereum bundles from searchers, if tx_i and tx_j conflict, as well as tx_j and tx_k conflict, then there is a high likelihood that tx_i and tx_k also conflict. This eases the constraints on the solution since, amongst an all-2-all graph of transactions, for MIS, you only need to pick the transaction with the highest utility (also satisfying knapsack).
Another thing to note is that our algorithms can inform how block builders construct blocks in practice. Notably, the Classical Greedy Informed algorithm, in which we sort the transactions by highest fee, is closest to the optimal solution.
That being said, the most exciting extension to this research would be modeling the block-building problem as a job sequencing problem instead and somehow estimating how utility (fee+MEV) from one transaction affects the utility of other transactions sequenced after the first transaction.
On that note, we invite potential collaborators to explore new ideas for building blocks that maximize the builders’ utility.