BlockFlow: introducing a novel sharding algorithm with single-step cross-shard transactions

Sharding
1

Hi All!

I am Cheng, founder of Alephium project. We found a novel sharding protocol which supports native cross-shard transactions, i.e. no two-phase commit is needed for cross-shard txs. We call it blockflow. It’s a general sharding algorithm, but the idea could be applied to Ethereum.

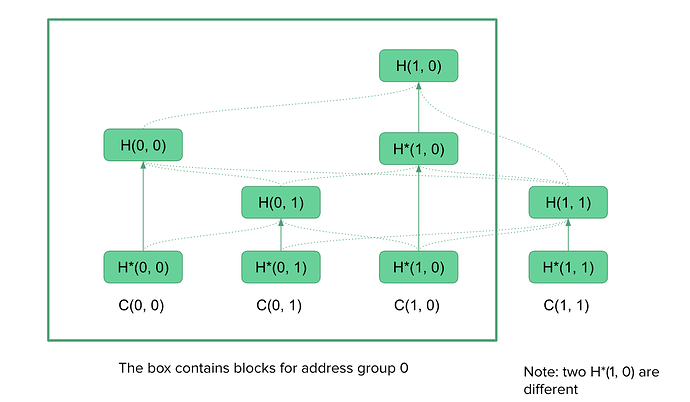
We briefly describe the ideas here. In blockflow, we first shard addresses into G groups, then we distribute all transactions into GxG shards based on the input address and output address. Let’s say that shard (i, j) consists of transactions from group i to group j. For group i, it only needs to download transactions from shards (j, i) and (i, j), so 2G-1 shards instead of GxG shards in total. This contributes to scalability. Transactions from group i to group j would be submitted directly to shards (i, j), which is probably the first approach that avoids two-phase commit.

We use a specific data structure + finality algorithm to reach consensus for all shards. Thanks to our data structure, the algorithm suffers from 51% attack instead of 1% attack. The cost of using this sharding algorithm is that it requires additional storage for the new data structure that stores shards dependencies, the cost is around 100B-200B per block. We don’t need a super node, but “full node” would consist of G node with one for each group to form a complete ledger.

We also have some innovative features for scaling smart contracts. We decompose smart contracts into a token part and a data part. Then, we provide a scripting language for token level programming. It’s a practical tradeoff as we don’t want to have a built-in VM language for the data part.

More details and proofs are available in our white paper. I’d welcome any questions and discussions! Or give us feedback via Twitter @alephium.

2

What about shard validators/collators? It seems like since any group i can interact with any other group j, validators need to store and verify all GxG cross-shard transactions, which would defeat the purpose of sharding.

3

No external validators/collators needed in this sharding approach, since the “full node” itself consists of G nodes could validate all blocks. Specifically, blocks handling transactions from group i to group j would be validated by the i-th subnode of a “full node”.

4

So do we expect to have everyone run a full-node? If my address is in i, surely I want to allow all addresses in the G space to be able to send me payments, no?

5

We do not expect everyone to run a full node. There would be full nodes and lightweight nodes like Bitcoin. Lightweight nodes would be good for lightweight wallets for ease of use. Full nodes are for users or businesses with high security demands.

G would be relatively small in the beginning when there are not so many participants. Then the system itself would gradually increase G along with time. Our current plan is to start with G=4 and then gradually increase to 8, 16, 32…

6

I’m having trouble understanding the protocol.

Going through the paper:

[introduction]

So the state is partitioned into G shards, with transactions partitioned into G^2 shards in a G * G grid where shard (i,j) can touch state in shards i and j.

The dependencies of H_{i, j} is d(H _{i,j} ) = \{H'_{i,j}\} \cup \{H'_{i,r}\}_{r \ne j} \cup \{H'_{k,l_k}\}_{k \ne i}

A block in some row or column has, as dependencies, (i) a block on every other column of the same row, and (ii) a block on some column on each of the other rows.

As written this suggests that eg. the newest block {3,5} has the newest block {3,4} as a dependency, and the newest block {3,4} also has the newest block {3,5} as dependency, so there are circular dependency relationships. Is this the intended reading, or are all dependencies non-circular?

Also, why is it just a block on some column on each of the other rows; why not restrict it to be the same column on each of the other rows?

Assume that H_{k,l_k} \rightarrow H_{k,l} (k \ne i, l \ne l_k) by definition. Let D(H_{i,j}) = d(H_{i,j}) \cup \{H_{k,l}\}_{k \ne i, l \ne l_k}

So far, this is saying that because a block has a dependency on every other row, and every other column, the second-order dependencies cover the entire G*G grid; correct? Also, because D(H) covers the entire grid, it can be seen as a view of the entire super-chain.

We say D(H_1) < D(H_2) if for all H_{a,b} \in D(H_1) and H*_{a,b} \in D(H_2) we have H_{a,b} < H*_{a,b}

So one view is a descendant of another view if every chain in that view is a descendant of every other chain in that view.

The rules for checking d(H_{i,j} )

What do you mean by “checking d(H_{i,j} ) ”?

Admissibility.

Would help to have more detailed descriptions of what each of these five conditions is checking. Also, where do these H*_{i,j} variables come from? Are these rules for comparing two forks to determine which fork is the correct canonical chain, or are they rules for validity?

7

Thanks for all the detailed feedback, very much appreciated.

So the state is partitioned into G shards, with transactions partitioned into G2 shards in a GxG grid where shard (i,j) can touch state in shards i and j.

There are GxG shards in the system, G is just the number of address groups. For each address group, there are G shards. In our setting, cross-shard transaction becomes cross-group transaction.

Our approach is not state-based, more like a token-based approach. It’s a crucial design trade-off we made in the beginning, as I found that scaling UTXOs+data is much easier than scaling state-based contracts. Applications could have state by using data blobs along with UTXOs. Some of the applications could even stick to shard (i, i) which would be almost the same as traditional blockchain. We definitely lose some generality for applications (second layer could help), but the gain is a much simpler scalable solution.

A block in some row or column has, as dependencies, (i) a block on every other column of the same row, and (ii) a block on some column on each of the other rows.
As written this suggests that eg. the newest block {3,5} has the newest block {3,4} as a dependency, and the newest block {3,4} also has the newest block {3,5} as dependency, so there are circular dependency relationships. Is this the intended reading, or are all dependencies non-circular?

The dependencies would form a directed acyclic graph. This DAG would be used to decide a fork for each shard.

In your example, the newest block {3, 5} would use the latest block {3, 4} as a dependency, and the newest block {3, 4} would use the latest block {3, 5} as dependency. These two newest blocks {3, 4} {3, 5} could be created at the same time. But later they could be used as dependencies together for the newest block {3, 1} for example.

Also, why is it just a block on some column on each of the other rows; why not restrict it to be the same column on each of the other rows?

As the block time is a bit random for different shards, we want to use the latest blocks from other rows, to include as much blocks as possible.

So far, this is saying that because a block has a dependency on every other row, and every other column, the second-order dependencies cover the entire G*G grid; correct? Also, because D(H)covers the entire grid, it can be seen as a view of the entire super-chain.

Yes, it’s supposed to decide a view for the entire super-chain which got distributed among G separate nodes. The dependencies construction would ensure the view is correct.

What do you mean by "checking d(Hi,j)"?

I meant the rules to follow when constructing d(Hi, j) and validating d(Hi, j). d(Hi, j) is the dependencies.

Would help to have more detailed descriptions of what each of these five conditions is checking. Also, where do these H∗i,j variables come from? Are these rules for comparing two forks to determine which fork is the correct canonical chain, or are they rules for validity?

Your guess is right here. The admissibility checking is to ensure that all the forks selected consistently depends on each other, e.g. no such case: fork {3, 4} depends on one fork of {3, 5}, while fork {3, 3} depends on another fork of {3, 5}.

P.S. To be honest, it’s not trivial to gives all the details written here. If you have time, I’d like to present our algorithm to you more in depth.

8

Your guess is right here

Still not understanding this. The rules are rules for “admissibility”. Admissibility of what? d(H_{i,j}) If so, then why not just say admissibility of H_{i,j}, since for a block to be admissible, its dependencies should also be admissible? Or is there a difference?

Also, where do these H*_{i,j} come from? Is there a “for all” qualifier here, ie. for all H*_{i,j} < H_{i,j}, if H*{i,j} \rightarrow H*_{i,r} for any H*_{i,r} then H*_{i,r} < H_{i,r}?

Maybe some diagrams perhaps for the maximally simple 2x2 case would help.

9

Still not understanding this. The rules are rules for “admissibility”. Admissibility of what? d(Hi,j) If so, then why not just say admissibility of Hi,j, since for a block to be admissible, its dependencies should also be admissible? Or is there a difference?

It’s the admissibility of d(Hi, j) which is not different from saying admissibility of Hi,j. The admissibility rules are only used for dependencies.

Also, where do these H∗i,j come from? Is there a “for all” qualifier here, ie. for all H∗i,j<Hi,j, if H∗i,j→H∗i,r for any H∗i,r then H∗i,r<Hi,r?

For me, “if” is equal to “for any” qualifier which then is equal to “for all” qualifier. So, I meant “for all” qualifier.

Maybe some diagrams perhaps for the maximally simple 2x2 case would help.

Here is a simple example for 2x2 case without forks for simplicity:

29
291458×850 55.1 KB