Hello ethresearch community,
this is my first (real) post, so please be lenient toward me.
Paper: research/papers/casper-basics/casper_basics.pdf at 2a94a123efab844662da3be9a086c9b944fbab9c · ethereum/research · GitHub (as of 2nd march 2020)
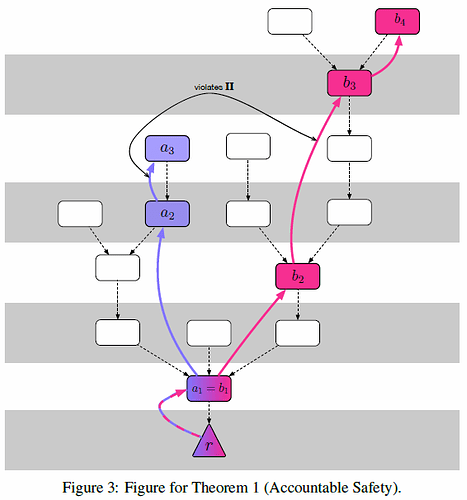
Theorem 1 (Accountable Safety). Two conflicting checkpoints a_m and b_n cannot both be finalized.
Let a_m (with justified direct child a_{m+1}) and b_n (with justified direct child b_{n+1}) be distinct finalized checkpoints as in Figure 3. Now suppose a_m and b_n conflict, and without loss of generality h(a_m) < h(b_n) (if h(a_m) = h(b_n), then it is clear that \frac{1}{3} of validators violated condition \textbf{I}). Let r \rightarrow b_1 \rightarrow b_2 \rightarrow \cdots \rightarrow b_n be a chain of checkpoints, such that there exists a supermajority link r \to b_1, \ldots, b_i \to b_{i+1}, \ldots, b_{n} \to b_{n+1}. We know that no h(b_i) equals either h(a_m) or h(a_{m+1}), because that violates property (iv). Let j be the lowest integer such that h(b_j) > h(a_{m+1}); then h(b_{j-1}) < h(a_m). However, this implies the existence of a supermajority link from a checkpoint with an epoch number less than h(a_m) to a checkpoint with an epoch number greater than h(a_{m+1}), which is incompatible with the supermajority link from a_m to a_{m+1}.
Casper Commandment I and II:
\textbf{I.} h(t_1) = h(t_2)
\textbf{II.} h(s_1) < h(s_2) < h(t_2) < h(t_1)
Figure 3 depicts the situation.
A problem I see is using the term “finalized” in the proof. Definition of “finalized”:
A checkpoint c is called \textit{finalized} if it is justified and there is a supermajority link c \to c^\prime where c^\prime is a \textit{direct child} of c. Equivalently, checkpoint c is finalized if and only if: checkpoint c is justified, there exists a supermajority link c \to c^\prime, checkpoints c and c^\prime are not conflicting, and h(c^\prime) = h(c) + 1.
And the definition of the height function h:
the height h(c) of a checkpoint c is the number of elements in the checkpoint chain stretching from c all the way back to root along the parent links
Using this definitions, b_n can not be a finalized checkpoint, even without Commandment II, since h(b_{n+1}) = h(b_n) + 3.
If the proof can stay in that form (I see that it’s valid if I am not strict with the terminology), I suggest to add “(Commandment II)” after the last word in the proof. Also I suggest to rename “condition I” to “Commandment I” in that proof.
Besides that, a general question:
If we take Figure 3 and remove the supermajority links on the blue path (left), the checkpoint chain on the pink path (right) would be valid. Nevertheless b_2 and b_3 would not be considered finalized. Is that volitional?
Edit: One more question, doesn’t a_3 already violate Commandment I, since h(a_3) = h(b_2)?