As it turns out, we can reduce the number of message types in Casper the Friendly Finality Gadget from two (prepares and commits) to just one (“votes”), increasing the algorithm’s simplicity to something which is arguably no longer that much more complex than, say, Nakamoto PoW.
A vote has three parameters:
- Epoch number
- Checkpoint hash
- Epoch source (MUST BE less than epoch number)
The two slashing conditions are as follows, using the notation (e1, h1, s1) or one prepare and (e2, h2, s2) for the second prepare. If a validator sends two prepares that satisfy either of these, they can lose their deposit.
- NO_DBL_VOTE: e1 = e2
- NO_SURROUND: e1 > e2 > s2 > s1
Alternatively, this can be expressed as one three-clause condition (thanks Virgil for the suggestion!):
def is_slashable(vote1, vote2):
if vote1.epoch > vote2.epoch:
return vote1.source < vote2.source
elif vote1.epoch < vote2.epoch:
return vote1.source > vote2.source
else:
return True
NO_DBL_VOTE can be expressed in English as “don’t contradict yourself within the same round”, and NO_SURROUND can be expressed as a prohibition against forgetting. That is, if you first vote (e1, s1), then later (e2, s2) (the epoch counter being an implicit clock, so we can assume e2 > e1), then it really should be the case that s2 >= s1, as otherwise you’re pretending not to know about s1, which you’ve already proven earlier that you know about).
We define a checkpoint as “justified” as follows:
- The genesis is justified.
- If a chain has accepted votes from 2/3 of validators for some checkpoint C that all use as a source the same ancestor C’, and C’ is justified, then C is justified
Note that in an actual implementation, the Casper smart contract only needs to keep track of votes within its own chain; this check can be done on the hash of C, and if that passes then the epoch source uniquely identifies C’; this is why we no longer need (and in fact never needed) to specify the source hash.
We define a checkpoint as “finalized” as follows:
- The genesis is finalized.
- If a checkpoint (i) is justified, (ii) has a direct child C’ that is justified, and (iii) the votes justifying C’ use C as a source, then C is finalized.
Here’s the safety proof:
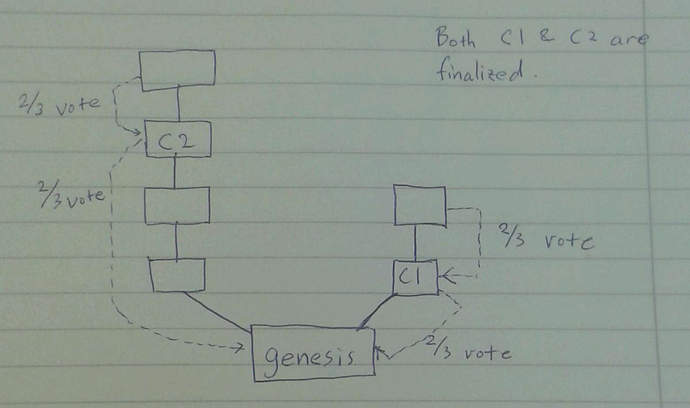
Suppose that two conflicting checkpoints C1 and C2 are finalized, and suppose e2 > e1 without loss of generality (if e2 = e1, then there is trivially an intersection of 1/3 of validators who voted for C2 and C1, which can be slashed with NO_DBL_VOTE). Consider the justification chain (ie. the chain of justified epochs along the chain from GENESIS to e2), e2, e2’, e2’’, e2’’’ … e2*, e2** … GENESIS, where e2** is the first item in the chain that is <= e1 and e2* the epoch justified with e2** as its source. Note that e2* >= e1+1 by definition. There are two cases:
- e2** = e1. Then, 1/3 get slashed with NO_DBL_VOTE
- e2* = e1+1. Then, 1/3 get slashed with NO_DBL_VOTE
- e2** < e1, e2* > e1+1. so there are 2/3 votes for (e2* > e1+1, e2** < e1). There are also 2/3 votes for (e1+1, e1). Hence, 1/3 are slashed by NO_SURROUND
Plausible liveness proof (can finalize new blocks assuming 2/3 compliant validators who do not use a non-justified checkpoint as an epoch source):
Let M1 be the highest justified epoch, and M2 be the highest epoch that anyone has prepared on. By the assumption, no one has made any prepares with epoch source higher than M1. Hence, 2/3 votes with epoch M3 > M2 and epoch source = M1 do not violate NO_DBL_VOTE or NO_SURROUND. Then another 2/3 votes on epoch M3 + 1 can finalize epoch M3.
We can also introduce a correct by construction fork choice rule: always choose the longest chain on top of the highest-epoch-number justified checkpoint. This is correct by construction because it follows along the logic of the liveness proof, which precisely states that attempting to finalize new checkpoints on top of the highest-epoch-number justified checkpoint is how new checkpoints can always be successfully finalized.
Note that a situation where C1 is finalized and C2, a non-descendant of C1 with a higher epoch number, is justified is impossible, and this can be proven with the same argument as the above safety proof. Hence, if we accept a 2/3 honest majority assumption, simply accepting the highest-epoch-number justified checkpoint actually works. If we do not accept such an assumption, then the simplest correction is to refuse to revert finalized blocks (note that this is time-dependent in that it will lead to permanent divergence if 1/3 equivocation does happen, but this is unavoidable).