Thanks for the thoughtful response. Enjoyed pondering the tradeoff exploration with respect to p.
Context
For reference, found the approach you’re referring to in the previous paper. You are right that it is a specific instance of: BP(TD, e - e_{LF}) = \frac{k_1}{TD^p} + k_2 * [log_2(e - e_{LF})] (Didn’t realize we had set on 1/2 for p)
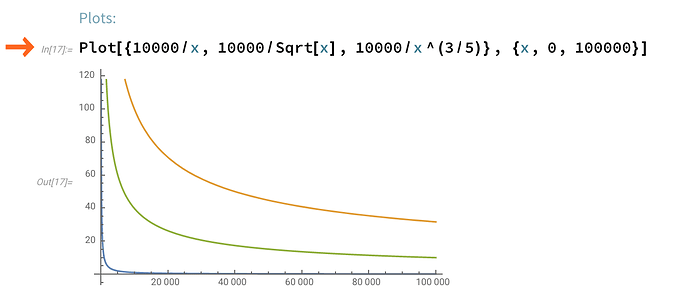
As we discuss, here are the plots for reference for various p values and constant k:
(blue is p = 1, green is p = 3/4, orange is p = 1/2)
Additional Consideration for p
While I will further study the merits of the p = 1/2 vs p = 1 approaches, the reason why I began thinking about the problem in p = 1 is for simplicity’s sake. For illustrative purposes, let’s consider modeling each case in the interest rate = constant / total deposits ^ p framework.
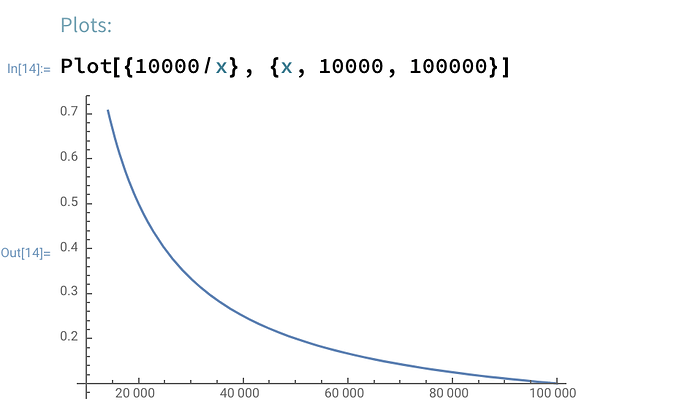
For p = 1, any k/TD value is simply the periodic interest rate. For instance, from {x, 10000, 100000} and k = 10000, we can observe the interest rate getting competed away from ~100% down to ~10% as more deposits enter the validator set (graph range truncated).
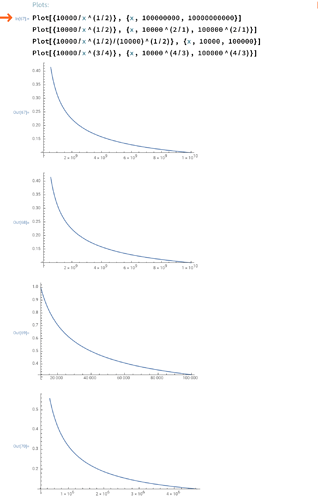
In contrast, we must apply a transformation to observe the TD to interest rate relationship for p = 1/2. More precisely, to observe the same drop in interest rate from 100% down to 10%, we have to adjust the x-axis by the \frac{1}{p}th power, or–alternatively–the function by a factor of k^\frac{1}{p} to observe the same order of magnitude change in interest rate.
While analytically straightforward, I found it less intuitive to reason about the interest rate to TD relationship for p = 1/2.
Takeaways
Perhaps a reasonable hybrid approach is to model the TD target in terms of p = 1, and as a final step we can dial in the desired convexity of the function around the desired TD and transform the k value accordingly.
We can find a p value that brings a gradual yet compelling ramp to the target TD level without being so “forceful”, which would likely create more deadweight losses than a “smoother ramp.” That said, I think it is important to err on the side of predictable TD and interest rate relationship to enable monetary policy decisions.
Furthermore, in the context of bootstrapping, we could use a very loose ramp (i.e. lower p-values) to make sure we’re not prescriptive about the required returns. This would allow us to more accurately assess the perceived required returns by the validator set. Once this is measured for a given mechanism, we can tighten up the ramp (i.e. higher p-values) to more accurately target a given TD level to secure the Ethereum network at any given market cap. (For example, if TD doesn’t grow alongside market cap, the implied economic security level could be capped and limit the growth potential of ETH long-term).