Check out Three Sigma’s new article, the first of a two-part series, about a novel approach to reduce and optimize Optimistic Rollup’s challenging periods.
Below, me and @AndreP3Sigma provide a brief introduction to this article.
Preface
Ethereum’s scalability challenge is a significant obstacle to its widespread adoption, which Layer-2 scaling solutions, like optimistic rollups, aim to address. Optimistic rollups aggregate transactions in batches off-chain, which are then submitted to Ethereum’s mainnet. However, this solution comes with its own set of challenges, such as the length of the challenging period and the use of a centralized sequencer. The length of the challenging period affects the security and efficiency of the system, while the choice between a centralized and decentralized sequencer impacts its reliability and control.
Solutions currently employ a 7-day challenging period, but no solid justification has been found for this value. It’s important to ask whether it makes sense that all types of transactions have the same challenging period. In fact, there may be a need to reduce the period according to transaction risk and sequencer history, while improving the user experience and maintaining security. This includes transitioning to a decentralized network of sequencers without, ideally, increasing L2 costs.
The first topic is introduced here.
Rationale for the Dynamic Challenging Period Model
The current 7-day challenging period is considered too long and expensive for a malicious sequencer to block the L1 network with invalid transaction batches. To prevent this, a challenging period should be set such that it is not profitable for a malicious sequencer to conduct a denial-of-service (DoS) attack on the network. Sequencer reputation and the aggregated value of the batch should be considered when determining the challenging period. A minimum challenging period should also be enforced to prevent invalid small-value transactions.
Furthermore, the challenging period of a given batch must end at the same time or after the previous batch to ensure that finalized batches imply the finality of previous batches. This condition is applied after a batch time is computed, as follows:
\mathrm{T_B} = \max\big\{\mathrm{CP_{min}}\ ,\ \mathrm{G_T} \cdot \min\{7 \ \text{days}\ ,\ \text{T}(\mathrm{S_{\text{Total Cost}}}= \mathrm{V_B})\}\big\}
where:
\text{CP}_\text{min}: The minimum challenging period required to submit a fraud proof for a given batch;
\text{T}(\mathrm{S_{\text{Total Cost}}}= \mathrm{V_B}): Function that gives the amount of time required for a malicious sequencer spend the same amount of value in a DoS attack that they could potentially earn from the aggregated value of the corresponding batch (\mathrm{V_B}).
\mathrm{G_T}: Governance-adjusted time factor (between a minimum threshold and 1), based on sequencer’s reputation, which will be addressed in a Part II of the series.
On top of this, the aforementioned condition of previous batches being finalized first must be applied. To gain a full understanding, refer to the corresponding section of the article.
Minimum Challenging Period
The discussion of how short the challenging period can be has already been brought up in 2020. Ethereum’s consensus mechanism was still Proof-of-Work, with a minimum of 4.5 hours being derived, assuming a 15-second block time. However, there were consensus failures lasting more than that. The minimum challenging period must not be shorter than this time range. If it were, a malicious sequencer could take advantage of the network’s instability and increase the likelihood of successfully submitting fraudulent batches in the mainnet.
For the current model, one of the first consensus failures in Ethereum’s blockchain, which lasted around 21 hours until its resolution, is considered. To determine the minimum challenging period, it was assumed that the probability of a malicious sequencer leading a successful DoS attack on the L1 network would decrease exponentially as the number of submitted blocks increases:
\mathrm{P_\text{sucessful DoS attack}}=\text{e}^{-A_1\cdot\, \mathrm{N_\text{blocks}}}
If the attack is to be successful in just one block, then one may consider that as a quasi-certain attack: \mathrm{P_\text{sucessful DoS attack}} = 99\% \implies A_1 = 0.001. Contrarily, if one assumes that an unlikely attack has \mathrm{P_\text{sucessful DoS attack}} = 0.1\%, then the attempt of attack has to be sustained for 6908 blocks. Given a 12-second block time, the equivalent time period is 23 hours. Considering it exceeds the 21-hour consensus failure resolution described, the minimum challenging period in the present model will be:
\mathrm{CP_{min}= 23\text{ hours}}
For more information on the results, please refer to section “Minimum Challenging Period” of our report.
Understanding the time for equalizing batch value with cost of spamming L1 network
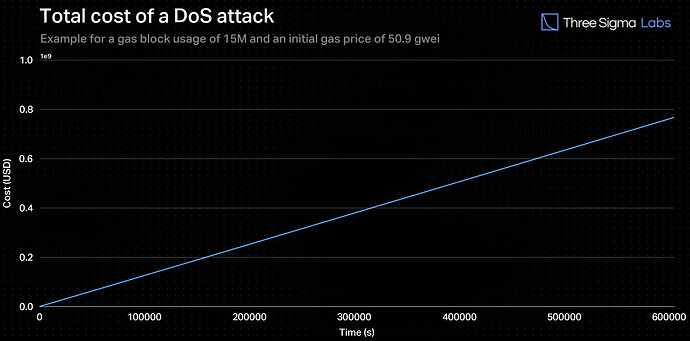
The goal of this section is to explain how to find the time required for a malicious sequencer to spend the same amount as possible earnings from an invalid batch during a DoS attack on Ethereum’s mainnet. The malicious sequencer submits transactions that are prioritized at the top of the block and consume all available gas to prevent other honest L1 network transactions (including fraud proofs) from being included in the blockchain. This creates an adversarial environment where gas prices increase as the malicious sequencer tries to outbid other traders in the mempool. Over time, fewer agents are willing to pay high fees, leading to less competition and a decrease in the rate of escalation of gas prices. Therefore, the evolution of gas prices, thus the transaction cost, over a large time scale, is considered to be logarithmic.
By integrating the transaction cost evolution function over time in a DoS attack, a total cost function was derived. This function represents the cost that a malicious sequencer would incur to spam the network for an increasing number of blocks. The function is given below:
\mathrm{S_{\text{Total Cost}}}= (t+10^{-2})\cdot 7.2222 \cdot \ln{(t + 10^{-2})}-t\cdot \big[7.2222\cdot (1+\ln(10^{-2}))-\text{GasPrice} \cdot \text{GasUsed}\big]+\text{GasPrice}\cdot \text{GasUsed}-7.2222\cdot 10^{-2}\cdot \ln(10^{-2})
where \text{GasPrice} is the price of gas at t=0, and \text{GasUsed} is the gas usage of a block, which may be considered equal to 15 million (regular limit).
Each time a batch is being submitted, the current gas price is obtained from an oracle and, by utilizing this function, the equation \mathrm{S_{\text{Total Cost}}}= \text{V}_\text{B} is solved and the corresponding value of \text{T} is computed. For example, with a initial gas price of 50.9 Gwei and block gas usage of 15 million, a batch with an aggregated value of 400 million USD will have a \text{T} of 88 hours.
For more information on the results, please refer to section “Understanding the time required for equalizing batch value with the cost of spamming L1 network” of our report.
Summary
Part I introduces the concept of the challenging period in optimistic rollups, during which users can dispute incorrect transactions. The length of this period affects system security and efficiency. The proposed dynamic model reduces the period based on transaction risk (and sequencer honesty, in Part II), improving user experience without compromising security. Potential attack vectors are addressed and a minimum challenging period of 23h is recommended. Lastly, the model estimates the time required to balance batch value with the cost of spamming the L1 network during a DoS attack by a malicious sequencer.
Check out the Twitter discussion at https://twitter.com/threesigma_xyz/status/1635676314609889282.
Next-up
Next week, Part II will be released. The following topics will be addressed:
- Governance-adjusted time factor (\mathrm{G_T});
- Decentralized Sequencer Network, based on a novel selection process;
- New economic incentive to attract sequencers and push them to be honest;
- Notes on malicious behaviour penalization and on how eigenlayer novel approach can be included.