Coded ZKP/FHE, a decentralized, collaborative, robust ZKP/FHE System

[0x1cc]

TL;DR

• For a ZKP/FHE task, we can decompose it into several subtasks.

• We introduce redundancy into subtasks such that the original task’s result can be decoded from a subset of the subtask results, treating uncompleted subtasks as erasures. This is similar to the erasure code design in DA.

• For a (n,k) coded ZKP/FHE system, we can decompose a ZKP/FHE task into n subtasks, with k \leq n subtask results, we can obtain the original task’s result.

• With this coded design, we can design a decentralized, collaborative, robust ZKP/FHE system.

Background

ZKP/FHE systems play a pivotal role in blockchain ecosystems, ensuring privacy and enabling cost-effective verification. However, the resource-intensive nature of ZKP generation and FHE computation presents a significant challenge. To address this, numerous distributed algorithms have been devised to enhance scalability and are now integral to ZKP/FHE mining pools.

For instance, complex ZKP tasks can be subdivided into smaller subtasks, which are then distributed across multiple nodes for parallel processing. However, the efficacy of existing distributed algorithms falls short in ensuring robustness, hindering the realization of decentralized and collaborative systems.

Consider a scenario where a ZKP task is divided into k subtasks and allocated to k distinct nodes. Should one of these nodes fail to respond promptly, the entire computation process is stalled. While redundancy mechanisms, such as assigning each subtask to two nodes, may mitigate this risk, vulnerabilities persist. Even with this redundancy, if both nodes assigned to a task fail to respond in a timely manner, computational delays ensue.

In summary, while distributed algorithms offer scalability benefits, their current limitations impede the development of resilient decentralized and collaborative ZKP/FHE systems. Addressing these shortcomings is essential for advancing the efficacy and reliability of such systems within blockchain environments.

Proposal

In this proposal, we introduce redundancy into subtasks to enhance the robustness of Zero-Knowledge Proof/Fully Homomorphic Encryption (ZKP/FHE) systems, akin to the erasure code design in Distributed Algorithms (DA). Specifically, in a (n,k) coded ZKP/FHE system, a ZKP/FHE task is decomposed into n subtasks, which are then distributed across n nodes. With a minimum of k completed subtask results, where k \leq n, the original task’s result can be obtained.

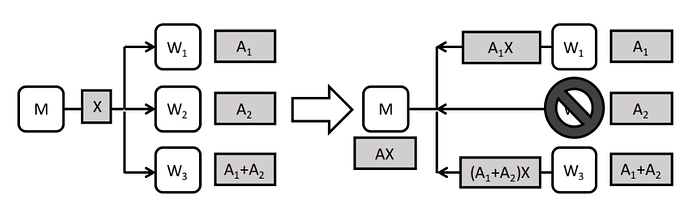
To illustrate this concept, let’s consider a toy model of matrix multiplication in zkML/fheML.

Consider a system comprising three worker nodes and one master node. In this setup, a data matrix A is divided into two submatrices, A_1 and A_2. Specifically, node W_1 stores A_1, node W_2 stores A_2, and node W_3 stores the sum A_1 + A_2. Upon receiving input X, each node computes the product of X with the respective stored matrix and transmits the result to the master node. Notably, the master node can reconstruct the product AX upon receiving any two products, thus obviating the need to await the slowest response. For instance, consider a scenario where the master node receives A_1X and (A_1 + A_2)X. Through subtracting A_1X from (A_1 + A_2)X, the master node can deduce A_2X and consequently reconstruct AX.

We can further adopt an (n,k) MDS code in this matrix multiplication example for generalization. For example, in zkML or fheML, we can adopt the (n,k) coded approach to design a decentralized, collaborative, robust ZKP/FHE System. In zkML, we can decompose the task into n subtasks, with the results and zkp of k subtasks, we can aggravate the zkp of these subtasks with the decoded process. In fheML, we can decompose the task into n subtasks, with the results of k subtasks, we can apply the fhe computation on the decoded process.

The preceding discussion has focused on a particular use case, namely zkML/fheML. The coded design methodology explored can be extrapolated to the foundational elements of the ZKP/FHE framework, facilitating the creation of a comprehensive coded ZKP/FHE system capable of supporting applications such as zkRollup and fheEVM computation.

Specifically, this coded approach can be applied to various components of the ZKP system, enabling the development of a distributed coded system. For instance, the R1CS instance in ZKP involves numerous multi-scalar multiplications, which can seamlessly integrate with the coded design. With the distributed computation algorithms applied in current distributed ZKP systems, we can further enhance the efficiency and scalability.

I may design and implement a PoC version of the coded ZKP system in my free time

Advantages

• This coded design significantly accelerates computation within ZKP/FHE systems. Theoretically, assuming a node count of n and subtask runtimes with exponential tails, the coded approach could be \theta(\log n) times faster than conventional uncoded distributed algorithms.

• With this coded design, the ZKP/FHE system is more robust. For example, in a (n,k) coded ZKP/FHE system, we can tolerate the downtime or delay of n-k nodes.

Applications

Utilizing the coded design paradigm, a ZKP/FHE mining pool can be devised, where decentralized agents function as worker nodes engaged in the computation of subtasks. The managerial role within this context is assumed by the manager of the mining pool, serving as the master node responsible for aggregating and decoding the results submitted by the worker nodes. Furthermore, the conventional master node architecture can be supplanted by a smart contract, assuming the duties of result aggregation and decoding. This architectural transformation facilitates the establishment of a decentralized, collaborative, and resilient ZKP/FHE system, wherein cryptographic operations are conducted in a distributed manner, enhancing the system’s robustness and scalability.

Conclusion

By breaking down ZKP/FHE tasks into subtasks and incorporating redundancy, a (n,k) coded ZKP/FHE system emerges, enabling the decomposition of tasks into n subtasks, with k \leq n subtask results required for task reconstruction. This coded approach facilitates the creation of decentralized, collaborative, and resilient ZKP/FHE systems, promising enhanced efficiency and reliability in cryptographic operations.

[fewwwww]

Interesting proposal, would like to get your insight on the following points:

• What would be the ideal/effective settings for k and n?
• I’ve seen ZKP designs and practices in the blockchain space, are their designs interchangeable with FHE? Or what’s the difference between generating “proof” for FHE and ZKP?
• Any materials on FHEML?

[Mirror]

I know RISC ZERO is doing this, so we can generate proofs in parallel.

[0x1cc]

I know RISC ZERO is doing this, so we can generate proofs in parallel.

Interesting! Does RISC0 also incorporate coding design into its ZKP generation process? From what I’ve seen, many ZKP projects utilize distributed algorithm to generate proofs in parallel and then aggregate the ZKP. However, without coding design, these distributed ZKP systems may lack robustness. I believe integrating coding design could serve as an additional mechanism to enhance the robustness and efficiency of existing distributed ZKP systems.

[0x1cc]

• What would be the ideal/effective settings for k and n?

The optimal design may vary depending on the specific case. From a mathematical perspective, we can frame it as an optimization problem and delve deeper into finding the optimal design.

• I’ve seen ZKP designs and practices in the blockchain space, are their designs interchangeable with FHE? Or what’s the difference between generating “proof” for FHE and ZKP?

From my perspective, the underlying systems of ZKP and FHE are distinct, so they may not be interchangeable. However, I bring up ZKP and FHE as examples because both are computationally intensive. Therefore, leveraging distributed or decentralized algorithms could enhance their efficiency. Additionally, their underlying systems might be suited for coding design. (zkML and fheML may be an example)

• Any materials on FHEML?

There isn’t a lot of material available on fheML at the moment. You can take a look at ZAMA’s related work on FHE.

[enricobottazzi]

I see that this k out of n idea fits with the matrix multiplication model you mentioned, but I’m not sure it will work for other tasks such as an EVM state transition (or even a simpler merkle tree state transition) Can you speak more about the requirement on the task such that it can fit into this model?

[idanieltam]

Overall, I believe this is a valuable and innovative proposal but we might need to validate:

1. Analyze on potential security implications. Even in ZK/FHE setting, the coded design introduces a new attack surface at the result aggregation level
2. Performance improvement. Theoretically the coded approach provide a θ(log n) speedup, but we need to verify each subtask result before reconstructing the final result

[0x1cc]

The “k out of n” coding design typically necessitates specific mathematical transformations. Matrix multiplication serves as a simple example of this concept. Designing such a coding scheme for general instructions like EVM state transitions poses significant challenges. However, it’s feasible to apply this coding design to cryptographic operations, such as multi-scalar multiplication and FFT.

The key lies in applying the coding design to all components and operators within cryptographic systems like ZKP/FHE. For instance, current approaches like zkEVM can generate zero-knowledge proofs (zkp) for EVM state transitions using ZKP systems. By extending the coding design to all computation components and operators within the ZKP system, we can create a distributed and coded ZKP system. And the generation of zero-knowledge proofs (ZKP) for EVM state transitions using this distributed and coded ZKP system can also be conducted in a decentralized, collaborative, and robust manner. Furthermore, leveraging this distributed and coded ZKP system as a foundation, various ZKP applications such as zkVM can reap the advantages of a decentralized, collaborative, and robust approach to proof generation.

[0x1cc]

1. Analyze on potential security implications. Even in ZK/FHE setting, the coded design introduces a new attack surface at the result aggregation level

With the coded design, before aggregating/decoding the results from subtasks, we also need to verify the correctness of the results of subtasks.

2. Performance improvement. Theoretically the coded approach provide a θ(log n) speedup, but we need to verify each subtask result before reconstructing the final result

This coding design does introduce some overhead. Theoretically, when the overhead is small enough (compared to the computation of the subtasks), we can achieve a \theta(\log n) speedup.

[zdanl]

Generally, I have no clue what the Ethereum mathematicans are even talking about, not to mention I can’t contribute or participate, but this seems compatible.

I’m working on a RISC emulating chain and would liek to enhance the robustness and overcome prohibitive cost of literally booting Linux on-chain, Cartesi, since I was told EWASM is dead as to Ethereum, and care to use a distributed binary translator / emulator. The single machine version of it is already breaking up computational workload into subtasks translating to IR in parallel.

Bit off topic, but so is Homomorphic Encryption as to Ethereum other than that Vitalik tweeted about it today Can you potentially help, with your math skill and train of thought, breaking down the unstoppable benefit of Linux VMs on-chain whileas the emulation is done distributedly; and potentially find a way to compute the cost, gwei, of such subtasks?

I like EVMs model of attaching a cost to single instructions, over the Cloud concept of renting Dedicated Cores hourly.

[enricobottazzi]

@0x1cc

However, it’s feasible to apply this coding design to cryptographic operations, such as multi-scalar multiplication and FFT.

I understand. It would be nice if you could PoC it on such fundamental level such that it doesn’t require an application specific setup. Even considering the setup in hashing based ZKP systems which might be tricky to distribute.

[cryptskii]

@enricobottazzi

It would be nice if you could PoC it on such fundamental level such that it doesn’t require an application specific setup. Even considering the setup in hashing based ZKP systems which might be tricky to distribute.

1. Segmentation and Hash Computation:

• Let A be the full dataset, divided into k segments: A_1, A_2, \ldots, A_k.
• Compute the hash H_i for each segment A_i.

2. Erasure Coding of Hashes:

• Apply an (n, k) MDS code to the vector of hashes \mathbf{H} = (H_1, H_2, \ldots, H_k).
• The coding process involves a generator matrix G of size n \times k. The encoded hashes are computed as follows:

\begin{bmatrix} \hat{H}_1 \\ \hat{H}_2 \\ \vdots \\ \hat{H}_n \end{bmatrix} = G \cdot \begin{bmatrix} H_1 \\ H_2 \\ \vdots \\ H_k \end{bmatrix}

• Here, \hat{H}_1, \hat{H}_2, \ldots, \hat{H}_n are the encoded hashes, distributed across n different nodes.

3. Reconstruction and Verification:

• From any k of the n encoded hashes, reconstruct the original hashes \mathbf{H} using the decoding process of the MDS code. This process relies on the inverse operations involving the subset of rows from G corresponding to the k available encoded hashes.
• Validate the data integrity by comparing the reconstructed hashes with the computed hashes from the received data segments.