TL;DR: In the past, it has been questioned whether Avalanche RANDAO and verifiable delay functions (vdfs) are compatible, because Avalanche RANDAO allows large parties in the staking pool a “lookahead” on the entropy, so that they can start the vdf computation early. However, this is actually only a problem if the vdf output can be used to bias the entropy. This is only possible during the “effective lookahead” period, the time difference between knowing the secret and being able to exert influence on it. For n=128, the effective lookahead period is 22-34 [p=0.01-0.001] reveal periods for an adversary controlling 40% of validators, and 41-55 reveal periods for one controlling 50% of validators.
Intro
Avalanche RANDAO [Avalanche RANDAO – a construction to minimize RANDAO biasability in the face of large coalitions of validators] is a construction to harden the commit-reveal RANDAO. Verifiable delay functions can be used for a similar purpose [Minimal VDF randomness beacon]. Can we combine these two approaches to have an even stronger randomness beacon?
Avalanche RANDAO effective lookahead period
We define the “effective lookahead” period as the number of reveal periods between the time that an adversary knows the result of the RANDAO (assuming everyone reveals) and the last committee that the adversary completely controls, which is the latest time at which they could influence the result.
If an adversary can compute the vdf result faster than the effective lookahead period, they can bias the result by choosing whether to reveal in the committee that they fully control. In most cases, the effective for adversaries controlling less than 50% of the validators is zero or negative: At the time that the secret is known to them, it is already too late to influence it (they do not fully control any of the committees that still has to reveal). But if a vdf is computed using the Avalanche RANDAO output, and the adversary cannot compute it faster than the effective lookahead period, then they will still be unable to bias the entropy.
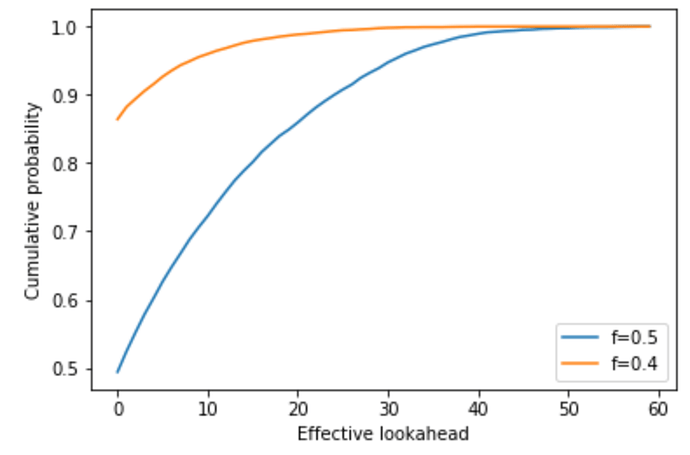
Using a Monte-Carlo simulation (python code below), we can find out the effective lookahead period. Below is a plot of the cumulative distribution functions at f=0.4 and f=0.5 for an n=128 Avalanche RANDAO. For n=128, the effective lookahead period is more than 22 reveal periods in only 1% of the cases and more than 34 in less than 0.1% for an adversary controlling 40% of validators. For an adversary controlling 50% of the validators, and it is 41 respectively 55 reveal periods.
Conclusion
The Avalanche RANDAO could be effectively combined with a vdf to get the best of both worlds:
-
Compared to the Avalanche RANDAO only, we can use the vdf to effectively prevent even adversaries controlling 50% of the validators from being able to bias the entropy
-
Compared to using the previous RANDAO+vdf construction, should the vdf be broken in some way, the underlying Avalanche RANDAO would still make the entropy safe in almost all cases.
The disadvantage of this construction compared to the RANDAO+vdf approach (apart from adding the Avalanche RANDAO complexity) is that the vdf would probably have to be timed for a longer period. However, if Avalanche RANDAO reveal timing is kept relatively short, for example 10 blocks, then target times of 220-550 blocks seem doable.
Python program for the Monte Carlo simulations:
import random
import math
import numpy as np
import matplotlib.pyplot as plt
def get_committee(layer, committee_no, compromised_nodes):
layer_subcommittee_size = 2 ** layer
committee = compromised_nodes[layer_subcommittee_size * committee_no:layer_subcommittee_size * (committee_no + 1)]
return committee
def check_committee_infiltrated(layer, committee_no, compromised_nodes):
return any(get_committee(layer, committee_no, compromised_nodes))
def check_committee_compromised(layer, committee_no, compromised_nodes):
return all(get_committee(layer, committee_no, compromised_nodes))
def layer_secret_known_after_reveal_no(layer, compromised_nodes):
layer_subcommittee_size = 2 ** layer
num_nodes = len(compromised_nodes)
for i in range(num_nodes / layer_subcommittee_size):
if all(check_committee_infiltrated(layer + 1, j, compromised_nodes) for j in range(i / 2)):
if all(check_committee_infiltrated(layer, j, compromised_nodes) for j in range(i, num_nodes / layer_subcommittee_size)):
return i
else:
return None
return None
def secret_known_after_reveal_no(compromised_nodes):
num_nodes = len(compromised_nodes)
num_layers = int(math.log(num_nodes) / math.log(2))
reveals = 0
for layer in range(num_layers + 1):
r = layer_secret_known_after_reveal_no(layer, compromised_nodes)
if r != None:
return reveals + r
reveals += 2**(num_layers - layer)
return reveals
def layer_last_influence_no(layer, compromised_nodes):
layer_subcommittee_size = 2 ** layer
num_nodes = len(compromised_nodes)
for i in range(num_nodes / layer_subcommittee_size - 1, -1, -1):
if check_committee_compromised(layer, i, compromised_nodes):
return i
return None
def last_influence_no(compromised_nodes):
num_nodes = len(compromised_nodes)
num_layers = int(math.log(num_nodes) / math.log(2))
reveals = 2 * num_nodes - 1
for layer in range(num_layers, -1, -1):
reveals -= 2**(num_layers - layer)
r = layer_last_influence_no(layer, compromised_nodes)
if r != None:
return reveals + r + 1
return None
def effective_lookahead(compromised_nodes):
ska = secret_known_after_reveal_no(compromised_nodes)
lin = last_influence_no(compromised_nodes)
if ska != None and lin != None and lin > ska:
return lin - ska
else:
return 0
def generate_random_compromised_notes(f, n):
return [1 if random.random() < f else 0 for i in range(n)]
n = 128
f4 = 0.4
f5 = 0.5
compromised_nodes_list4 = [generate_random_compromised_notes(f4,n) for i in range(10000)]
compromised_nodes_list5 = [generate_random_compromised_notes(f5,n) for i in range(10000)]
results4 = map(effective_lookahead, compromised_nodes_list4)
results5 = map(effective_lookahead, compromised_nodes_list5)
hist4 = [sum(1.0 if x == i else 0.0 for x in results4) / len(results4) for i in range(2*n)]
cdf4 = [sum(x for x in hist4[:i + 1]) for i in range(2*n)]
hist5 = [sum(1.0 if x == i else 0.0 for x in results5) / len(results5) for i in range(2*n)]
cdf5 = [sum(x for x in hist5[:i + 1]) for i in range(2*n)]
plt.plot(np.array(cdf5[:60]), label="f=0.5")
plt.plot(np.array(cdf4[:60]), label="f=0.4")
plt.legend()
plt.xlabel("Effective lookahead")
plt.ylabel("Cumulative probability")
plt.show()