Construction of Perpetuals AMM Protocol

Decentralized exchanges
1

Following up on this old discussion, we propose a construction of leverage perpetual AMM liquidity pools using an asymptotic power curve pair.

Asymptotic Power Curves
Asymptotic Power Curves3840Ă—2912 382 KB

Necessary differences from conventional unique-position perpetual exchanges:

  • payoff function is compound leverage {P\over{M}}^K instead of constant leverage M+K\times(P-M)
  • smooth Auto-Deleverage curve instead of manual ADL cutoff.

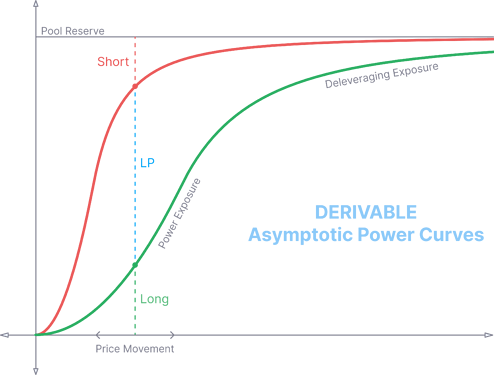
Derivative Payoff Functions

At any time or market state, the pool reserve is split between 3 sides: r_A, r_B and r_C. With P as the index price feed from an external oracle and M is a constant mark price selected by a pool, we have: x = {P\over M}

Long payoff:

r_A=\begin{cases} ax^K &\quad\text{for }ax^K\le{R\over 2} \\ R-\dfrac{R^2}{4ax^K} &\quad\text{otherwise} \end{cases}

Short payoff:

r_B=\begin{cases} bx^{-K} &\quad\text{for }bx^{-K}\le{R\over 2} \\ R-\dfrac{R^2}{4bx^{-K}} &\quad\text{otherwise} \end{cases}

LP payoff:

r_C = R - r_A - r_B

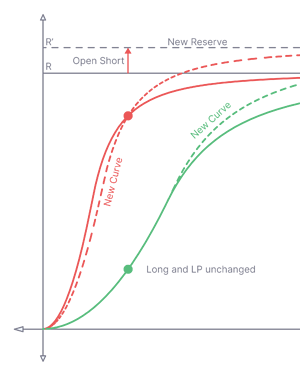
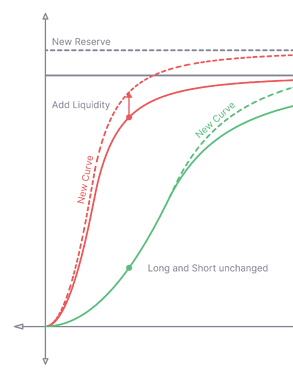
State Transition

A pool state is represented by a 3-tuple ⟨R,α,β⟩, and it can be changed by user transactions.

image
image2006Ă—2506 203 KB
image
image1998Ă—2554 207 KB

State transition can change the curves which affect the effective leverage of its derivative tokens but can not change the value of other existing “positions” in the pool.

Paper

In this whitepaper, our analysis demonstrates that, when properly initialized, the derivative tokens are optimally exposed to both sides of power leverages, and the market provides infinite liquidity in all market conditions, rendering it everlasting.

2 Likes