Cross-shard Transaction Probabilistic Simulation

Sharding
1

As part of researching cross-shard transactions the TXRX research team has built a cross-shard transaction simulator named Vorpal.

All of the probabilistically generated data can be found here: https://drive.google.com/drive/folders/1sloCwAnJ2Ok2zkuwjtBaFbyZdag-z4Dy?usp=sharing

Throughput is tracked using two metrics, transactions and transaction segments detailed in this previous research post. Transaction segments are portions of a transaction that result from a cross-shard call, where the transaction is the encapsulation of all the transaction segments.

How cross-shard transaction probabilities are calculated. After each transaction segment the cross-shard probability is recomputed resulting in a decaying probability for the encapsulating transaction.

Below is an example of a cross-shard probability calculation at a probability = 0.99, and the x axis is the resulting transaction segments

Test: Probabilistic cross-shard sweep

This test is a sweep of the --crossshard value from 0.0 - 0.99 over multiple simulations. --crossshard is the probability a cross-shard call will occur within a transaction.

Results

Configuration

collision_rate	0.0113712
	
shards	64
slot	12
blocksize	512
witnesssize	256
transactionsize	1
tps	10000
duration	500
probability 0.0 - 0.99
collision	0.01
sweep	FALSE
generate	FALSE
output	None
outputtransactions	None
input	None

Conclusion

As the probability of a cross-shard transaction increases linearly there is an exponential decrease in transactional throughput. At the maximum value of a cross-shard probability = 0.99 represents a ~0.503 proportional decrease in transaction throughput.

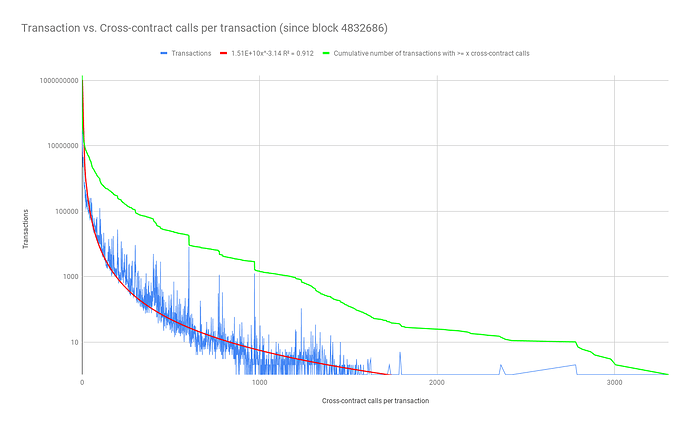
An average Eth1 transaction contains ~1.33 cross-contract call per transaction.

Assuming shards will have a uniform distribution of contracts the probability of a cross contract call resulting in a cross-shard transaction is 63/64 = ~0.984375 which is very close to the right hand side of this exponential slope. Resulting in ~1.315 cross-shard calls per transaction without any contract modifications or load balancing.

Recommendations

As a recommendation contract yanking should be implemented as part of the protocol to allow shard balancing.

Cross-shard calls should be economically priced to incentivize the utilization of contract yanking.

Next Steps

As part of this research the next steps will be to run Eth1 transactions into the simulator to capture non-probabilistic scenarios. Additionally, contract yanking will be tested to detect if there is a improvement in transactional throughput. Investigate in-protocol control loop based contract yanking.

6 Likes
2

I couldn’t interpret this graph. Maybe I’m missing something. @Joseph Could you please give more details?

1 Like
3

probability is a the probability that an encapsulating transaction will result in a cross-shard call, in this instance 0.99. The simulator uses that value to generate a random number weighted 0.99 for true that the transaction will result in cross-shard call. These cross-shard calls are called transaction segments in the write up.

If the transaction results in a cross-shard call the value probability is recomputed probability = probability/2 and applied again to the transaction. That gives us the decaying slope of probability for a single transaction.

Does that help?

4

Thanks for the details!

An important assumption here is that the probability of x-shard calls is halved in every successive transaction segments, which is a specific usage pattern. An interesting future analysis would be comparing the results for different usage patterns, which are parameterized here by the “probability of the a x-shard call in the next transaction segment” variable. Some probability distributions of interest:

  • Uniform
  • Exponentially decreasing (already modeled by the current simulation)
  • Exponentially increasing: A DoS pattern, where transaction segments are more and more likely to cause a new x-shard call (until the transaction runs out of gas, which can be modeled as a hard limit on # of segments in a transaction)
  • Normal(-like) distribution: This would make transactions aim for a average # of segments, after which the probability for new x-shard calls decreases
5

I am currently analyzing those to create a better simulation, however it would not effect the throughput results in a meaningful way. The current best research can be seen below:

Transaction vs. Cross-contract calls per transaction (since block 4832686) (3)
Transaction vs. Cross-contract calls per transaction (since block 4832686) (3)1238Ă—765 53.7 KB

There are actually two probabilities at play in a cross-shard call. The first is the probability that a transaction will result in a cross-contract call where from != to && from != EOA && to != EOA. That give the probability that a cross-contract call occurs in a transaction. This data is currently obtainable from Eth1.

The cross-contract call is then computed against a probability of the contract sharing the same shard in a uniform case is which is 63/64 = false. I am currently enhancing my simulator to account for different non-uniform distributions as you suggested. I am planning a third update on this topic following further analysis.

2 Likes