Cryptographic Obfuscation for Smart Contracts: Trustless Bitcoin Bridge and More

[SoraSuegami]

Author: Sora Suegami
This post is a summary of the following paper. Note that some corrections are not yet reflected in the published paper.

Cryptographic obfuscation for smart contracts: Trustless bitcoin bridge and more

Abstract

We propose a cryptographic obfuscation scheme for smart contracts based on existing Proof-of-Stake (POS) blockchain mechanisms, standard cryptographic assumptions, and witness encryption. The proposed scheme protects the privacy of smart contracts that access multiuser secrets without relying on an honest majority of SMPC participants or TEE. Users in the proposed scheme can provide an obfuscated smart contract with encrypted inputs and allow an untrusted third party to execute it. Although MPC among dynamically changing users is necessary, its privacy is protected if at least one user is honest. If the MPC does not finish within a period time, anyone can cancel and restart it. The proposed scheme also supports decentralized obfuscation where even the participants of the obfuscation process cannot learn secrets in the obfuscated smart contract unless all of them are malicious. As its applications, we present a new trustless bitcoin bridge mechanism that exposes no secret key and privacy-preserving anti-money laundering built into smart contracts.

Introduction

Privacy-preserving smart contracts protect data and function privacies. The former is the privacy for input and state data of the smart contract, whereas the latter is the privacy for the smart contract algorithm and secrets hardcoded in its bytecode. However, in existing solutions for privacy-preserving smart contracts, NIZK-based ones only support a limited class of smart contracts where only a single user’s secrets are handled simultaneously, and SMPC- and TEE-based ones rely on noncryptographic assumptions for their security, i.e., an honest majority of SMPC participants and trusted hardware. Cryptographic obfuscation could yield a new solution for smart contracts that access multiuser secrets and whose security does not depend on such third parties or hardware.

Obfuscation is a technique to hide the contents of a program while preserving its functionality. As such, anyone can execute an obfuscated program and obtain the same output as the source program, but they cannot know the algorithms or secrets included in the program. Cryptographic obfuscation is an obfuscation realized by cryptographic techniques, and its security is based on cryptographic assumptions. It can be used, for example, by software developers to distribute demo versions with limited functionalities to prevent reverse engineering of their software.

A smart contract that protects data and functions is constructed by hardcoding the secret key in its bytecode and obfuscating it with cryptographic obfuscation [1]. Transaction and state data are encrypted under the public key, and they are decrypted inside the obfuscated program. Its function privacy is directly guaranteed by the obfuscation security. Its data privacy is also guaranteed because an adversary cannot extract the hardcoded secret key from the obfuscated program. Therefore, cryptographic obfuscation enables a smart contract to cryptographically protect data and function without requiring an honest majority of the SMPC participants or TEE.

However, there is no cryptographic obfuscation that makes an arbitrary program a black box [2]. Instead, cryptographic obfuscation that guarantees weak indistinguishability, called indistinguishability obfuscation (iO), would be feasible. Recently, many iO candidates have been proposed, particularly in [3-4], which showed that iO can be constructed based solely on already established cryptographic assumptions. Unfortunately, even in the latest research [3-7], its efficiency is far from practical.

In addition to its inefficiency, iO is unsuitable to construct an obfuscated smart contract for two reasons. First, its privacy protection is limited because iO only guarantees the indistinguishability of two programs that have the same size and functionality (input-output relationship). That is, it only protects the function privacy for a smart contract that can theoretically realize the same functionality without a secret algorithm and values. Second, a smart contract can preserve a state, whereas iO cannot do that as it always returns the same output for the same input. Assuming that a smart contract obfuscated with iO takes as input a previous state and outputs a new state, we can provide any state as input to the obfuscated smart contract. As such, already provided states cannot be rejected. However, a smart contract, by specification, cannot use any state other than the latest one, so we have to resolve this difference.

Our Contribution

We propose a smart contract obfuscation (SCO) scheme that solves the above problems. Our scheme is characterized by the following points.

• It protects data and functions for wider classes of functions than iO.
• It uses existing proof-of-stake (POS) blockchain mechanisms without modifying their protocols.
• Although its users need to perform multiparty computation (MPC) to provide new encrypted inputs for an obfuscated smart contract, its security maintains if at least one of the users is honest. Furthermore, the users do not need to work after finishing a single encryption process. If the MPC does not finish within a period time, anyone can cancel and restart it.
• It can preserve the state of an obfuscated smart contract, that is, only the latest state can be provided as the input.
• It can obfuscate a smart contract in a decentralized manner; provided two smart contracts whose outputs are indistinguishable, no one can identify which is obfuscated and learn secrets hardcoded in the obfuscated smart contract unless all participants of the MPC for the obfuscation process are malicious.

The differences between previous works and this work are summarized in Table 1.

Definition and Security

System Model

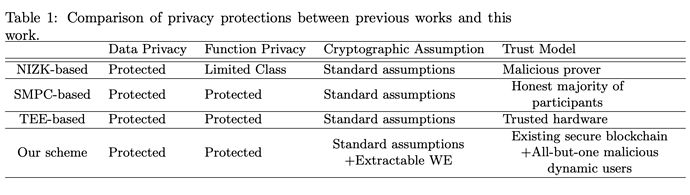
There are three roles for the SCO participants: an obfuscator, a user, and an evaluator (Figure 1). The obfuscator publishes an obfuscated smart contract and an encryption key. The user encrypts the user’s input with the encryption key and sends it to the evaluator. The evaluator evaluates the obfuscated smart contract on the encrypted input. The obfuscated smart contract comprises an obfuscated program and an on-chain program. The obfuscated program is an obfuscated probabilistic circuit C_{sc} \in \mathcal{C}_{n,m} that represents functions of the smart contract (defined as a contract circuit). An on-chain program is a bytecode deployed on the blockchain. Its input and state are available to participants of the blockchain network and executed by the associated transactions.

Compared to the architecture of ZKRollup, the role of the obfuscator is similar to that of a developer who creates a ZKP circuit for each application and deploys those proving and verifying keys. As with an operator in ZKRollup, there is no need to trust or constantly rely on the evaluator because anyone can evaluate the obfuscated circuit without learning anything about the encrypted input, state data, or bytecode.

The contract circuit handles a state \textsf{state} and a nonce nc, where nc is a number that indicates how many times the circuit has been evaluated. Formally, it takes as input a values y, a previous state \textsf{state}_{pre}, a nonce nc and the randomness r, and returns an output z, an updated state \textsf{state}_{new}, and an increased nonce nc+1. When C_{sc} is obfuscated, its encrypted state and nonce are included in the obfuscated circuit and updated for each evaluation.

The SCO scheme provides the following algorithms.

• Obfuscate(1^\lambda, N, C_{sc}, \textsf{state}_0; r): Takes as input a security parameter \lambda, a natural number N that denotes the number of users who provide inputs at the same nonce, a contract circuit C_{sc}, an initial state \textsf{state}_0 and the randomness r and outputs an obfuscated circuit \tilde{C_{sc}}, an encryption key ek, and a trapdoor td.

• Enc(ek, \vec{y};r): Takes as input an encryption key ek, N inputs \vec{y}=(y_i)_{i \in [N]}, and the randomness r and outputs a ciphertext ct_y.

• Eval(\tilde{C_{sc}}, ct_y): Takes as input an obfuscated circuit \tilde{C_{sc}} and a ciphertext ct_y and returns N output \vec{z}=(z^i)_{i \in [N]} and an updated circuit \tilde{C_{sc}}^{'} or the symbol \bot. The updated circuit includes the encryption of the updated state and nonce, and it is used as \tilde{C_{sc}} in the next execution of this algorithm.

Security Definition

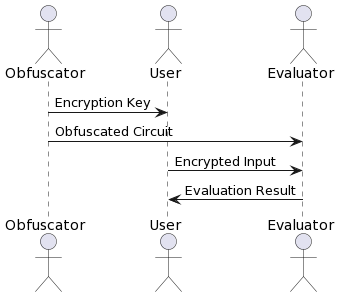
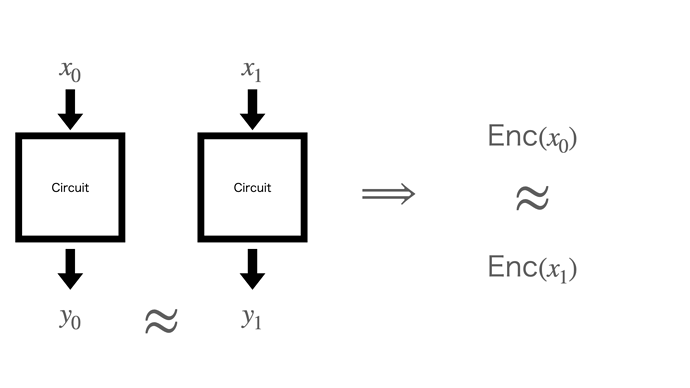
We define data and function privacies of the SCO scheme as input and function indistinguishabilities, respectively. Informally, the former definition guarantees that two encrypted inputs are indistinguishable, provided an adversary cannot distinguish their outputs (Figure 2). The latter definition guarantees that two obfuscated circuits are indistinguishable, provided their outputs are indistinguishable for the same input (Figure 3). Notably, as the contract process is represented as a probabilistic circuit, its output for the same input varies depending on the provided randomness. This allows for more relaxed requirements for circuits to be obfuscated than iO; although iO guarantees indistinguishability only for two circuits whose output is always the same for the same input, our scheme guarantees it, provided the two outputs are indistinguishable. For example, if two circuits output encryptions of different values, an adversary who does not know the secret key required to decrypt them cannot distinguish their outputs. Therefore, our scheme can make them indistinguishable, although iO can not do that.

Security Assumptions

Our construction of the SCO scheme satisfies the input and function indistinguishabilities under cryptographic assumptions and trust models as follows.

1. Cryptographic assumptions:

• Existence of one-way function.
• LWE assumption.
• Extractable secure witness encryption (WE).

2. Trust models:

• An honest majority of validators in existing POS blockchain.
• All-but-one malicious dynamic users.

The WE scheme still requires nonstandard ones except constructions through iO. In more detail, most of its candidates depend on multilinear maps [8-10], iO [11-14], or heuristics assumptions [15-17]. Therefore, unless using iO that is solely based on the standard cryptographic assumptions [3-4], our scheme also requires nonstandard ones.

To supplement the explanation for the last trust model, the user in our SCO construction must perform an MPC to encrypt their inputs at the same nonce. It seems to have the same downsides as the SMPC-based solutions for privacy-preserving smart contracts. However, our trust model is weaker than that of the SMPC-based solutions for the following three reasons.

1. Our scheme is secure unless all of the users in the MPC are malicious.

2. Our scheme allows for dynamic changes in the users participating in the MPC. In the most extreme case, our scheme is feasible even if all users do not participate in the MPC more than once.

3. If some users go offline and the MPC does not finish within a period time, new users can cancel and restart it at the same nonce.

The second and third features are possible because there is no common secret between users participating in different MPCs.

Notably, RANDAO relies on a similar trust model [18]. It generates unpredictable random numbers from the independent random numbers provided by multiple participants. Specifically, each participant generates a fresh random number and records its hash value onto the blockchain in the first round. After a sufficient number of the hash values are published, the participant reveals its random number in the second round. When all random numbers are revealed, RANDAO derives a new random number from the provided random number and registers it in the storage of RANDAO. If at least one participant is honest and does not reveal the random number until the second round, no malicious participant can force RANDAO to register the predicated random number; thus, it is secure against the all-but-one malicious participants. Furthermore, the participants in RANDAO are also dynamic and can restart a new process when one or more participants do not reveal the random numbers in the second round within a period time.

Decentralized Obfuscation

An obfuscator in our scheme can break its privacy protection because it knows all secrets hardcoded inside the obfuscated circuit. Therefore, instead of relying on a single trusted obfuscator, we employ obfuscator decentralization using MPC.

In the MPC, two contract circuits with indistinguishable outputs are shared among the participants. Only one of them is chosen and obfuscated randomly with the randomness unknown to any MPC participant. To compute it without exposing anything but the obfuscated circuit, the MPC participants homomorphically perform the obfuscation process in the MKFHE scheme. Specifically, each participant first generates the fresh randomness and publishes its encryption. The participants then homomorphically choose one circuit and obfuscate it using the XOR of their randomness. They finally publish the decryption shares for the encryption of the obfuscated circuit. Those shares recover the obfuscated circuit.

Using the above mechanism, if at least one of the MPC participants is honest, no participant can learn the hardcoded secrets and break the privacy protection of the obfuscated smart contract.

Application

Novel applications built with the SCO scheme are based on a smart secret key (SSK), a secret key that is privately stored and used by an obfuscated smart contract. The SSK is not revealed to anyone and is controlled only by the algorithm of the obfuscated smart contract. This allows the SSK to be treated as if it were a secret key managed by a trusted third party.

We present application examples of our SCO scheme: a trustless bitcoin bridge mechanism that exposes no secret key and privacy-preserving anti-money laundering built into smart contracts.

Trustless Bitcoin Bridge Mechanism Exposing No Secret Key

The bitcoin bridge mechanism allows bitcoin users to transfer bitcoins between Bitcoin blockchain and other blockchains, e.g., Ethereum blockchain. Crypto assets named Wrapped BTC (WBTC) are but one application using this mechanism [19]. The custodian of WBTC offers users the service of converting bitcoins on Bitcoin blockchain and WBTC tokens on Ethereum blockchain to each other as follows [20].

1. Deposit bitcoins: The user sends bitcoins to a custodian’s bitcoin address called the deposit address.
2. Mint WBTC tokens: After confirming the user’s transaction on Bitcoin blockchain, the custodian makes a transaction to mint WBTC tokens on Ethereum blockchain for an amount equal to the deposited bitcoins. This increases the user’s WBTC tokens balance.
3. Redeem WBTC tokens: The user makes a transaction to redeem the user’s WBTC tokens on Ethereum blockchain. This decreases the user’s WBTC tokens balance.
4. Release bitcoins: After confirming the user’s transaction on Ethereum blockchain, the custodian releases the bitcoins to the user for an amount equal to the redeemed WBTC tokens.

The trustless bitcoin bridge mechanism establishes a new WBTC token that does not rely on “a custodian or an individual that provides excessive collateral [21]”. As noted in [21], the difficulty in implementing such a mechanism lies in the lack of functionality supported by the Bitcoin script, a scripting system for transactions used in Bitcoin blockchain [22]. Specifically, transactions on Bitcoin blockchain can be verified on Ethereum blockchain using the NIZK proof system, but not vice versa because the Bitcoin script only supports basic cryptographic schemes [21]. The solution in [21] overcomes this problem by encrypting the secret key of the deposit address under the WE scheme. To decrypt that encryption, Ethereum blockchain data including a transaction to redeem the user’s WBTC tokens is necessary as a witness. Using the decrypted secret key, the user can make a transaction to send the deposited bitcoins to the user’s bitcoin address. As the Bitcoin blockchain only needs to verify the digital signature generated with the secret key of the deposit address, that solution can be built with the current Bitcoin script.

However, as the solution in [21] directly exposes the secret key of the deposit address, it forces the user to deal with the following two inconveniences.

• The user itself needs to download the ciphertext of the WE scheme and perform its decryption; that is to say, it cannot offload the decryption process to third parties.
• As the user can send all bitcoins tied to the secret key, the amount of bitcoins that the user can release is fixed within the service. In other words, the user cannot convert WBTC tokens for less than the amount of bitcoins associated with a single deposit address.

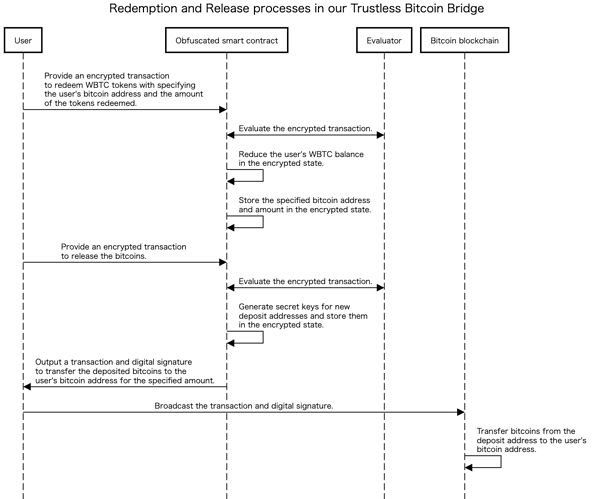
A new trustless bitcoin bridge mechanism is constructed from the SCO scheme to solve these inconveniences (Figure 4). We consider an obfuscated smart contract that randomly generates a secret key of the deposit address from the provided randomness and maintains the key and the users’ WBTC balances as its encrypted state. When a user requests the redemption of WBTC tokens, specifying the user’s bitcoin address and the amount of the tokens redeemed, the obfuscated smart contract reduces the user’s balance and stores that bitcoin address and amount. The user then requests the release of bitcoins to the obfuscated smart contract, which generates a new deposit address and outputs a transaction and digital signature to transfer the deposited bitcoins to the user’s bitcoin address for the specified amount and any other amount to the new deposit address. This way, our trustless bitcoin bridge mechanism only reveals the transaction and its digital signature, and the secret key of the deposit address remains secret. As no one can forge a digital signature for the altered transaction, the user can offload the evaluation of the obfuscated smart contract to third parties. For the same reason, the amount of bitcoins released need not be fixed.

In the above description, a contract circuit C_{\textsf{WBTC}} for our trustless bitcoin bridge mechanism generates a digital signature using a secret key of the deposit address stored in its encrypted state. However, since our SCO scheme only guarantees the input and function indistinguishability, we cannot directly prove that no adversary can extract the secret key from the obfuscated contract circuit. To overcome this problem, we introduce a traceable ring signature [23]. Given multiple public keys and a message, a ring signature verifier can verify that the holder of the secret key corresponding to any of the public keys signed the message but cannot identify which secret key was used. In addition, if the ring signature is traceable, the verifier can link two different messages signed with the same secret key [23-24]. Considering a contract circuit that stores two secret keys sk_0, sk_1 and outputs a traceable ring signature generated with one of these secret keys, we can prove that an adversary can extract no secret key from the obfuscated contract circuit as follows:

1. From the anonymity guarantees of the ring signature, the output of the contract circuit that depends on the first secret key sk_0 is indistinguishable from that of the second secret key sk_1.

2. From the function indistinguishability of the SCO scheme, the obfuscations of those circuits are indistinguishable.

3. Suppose an extractor of the secret key exists, an adversary can distinguish between those obfuscations by (1) generating a ring signature for a random message with the extracted secret key and (2) identifying whether the two messages signed by the obfuscated contract circuit and the adversary are linked with the ring signatures. Therefore, assuming the function indistinguishability of the SCO scheme, such an extractor does not exist.

When the above approach is applied to the contract circuit for our trustless bitcoin bridge mechanism, the deposit address is linked to two public keys (pk_0, pk_1), and its deposited bitcoin is released with a ring signature. Although the Bitcoin script does not naively support the verification of traceable ring signatures in a straightforward manner [22], it is feasible with the one-time traceable ring signatures proposed in [23]. Specifically, from Theorem 1 of [23], its verification algorithm is constructed from the following components under the random oracle model.

• Conditional branch.
• A PRG scheme with expansion from \lambda to 3\lambda bits.
• Hash function, such as SHA256 algorithm.
• XOR operation.

The first and third components are directly supported by opcode 99 and 168 of the Bitcoin script, respectively [22]. The second component is also feasible because PRG is constructed from a one-way function, e.g., hash function [25-28]. The fourth component, the XOR of two bits a \oplus b, is computed by combing the NOT, AND, and OR operations of opcode 145, 154, and 155, respectively, i.e., a \oplus b = (a \land \lnot b) \lor (\lnot a \land b) [22]. For the above reasons, the one-time traceable ring signature is compatible with Bitcoin blockchain.

The obfuscated circuit is generated via decentralized obfuscation for the circuits C_{\textsf{WBTC}}^0 and C_{\textsf{WBTC}}^1, where C_{\textsf{WBTC}}^0 and C_{\textsf{WBTC}}^1 uses sk_0 and sk_1, respectively, to generate the ring signature. From the security of the decentralized obfuscation, no obfuscator can learn the randomness used to generate those secret keys and which circuit is obfuscated. Therefore, the secret key of the deposit address is not revealed even to the obfuscators.

Smart Contract Built-in Privacy-Preserving Anti-Money Laundering

Our second application is the privacy-preserving anti-money laundering (AML) built into smart contracts. It is difficult to reconcile privacy protection and regulatory compliance for smart contracts. For example, the Office of Foreign Assets Control sanctioned Tornado Cash, a mixer protocol on the Ethereum blockchain [29] because it was used for laundering the stolen crypto assets [30]. Our SCO scheme could mitigate this tradeoff; that is to say, it protects the privacy of legitimate transactions, and at the same time, it allows for reporting to regulators those defined as illegal by a predefined algorithm. Specifically, we present a wallet service for crypto assets that satisfies the following properties:

• Report of illegal transactions: For each transaction, it executes an AML algorithm. If its algorithm determines that the transaction is illegal, it outputs a report encrypted with the regulator’s public key.
• Privacy against a regulator: If the AML algorithm determines a user’s transactions to be legal, it does not disclose information about the user’s transactions and balances to the regulator.
• Privacy against users: The users cannot learn the specifications of the AML algorithm.

A contract circuit C_{\textsf{Wallet}} for our wallet service stores an AML circuit C_{\textsf{AML}} that outputs 1 if the provided transaction data is illegal and 0 otherwise in its encrypted state. When C_{\textsf{AML}} outputs 1, C_{\textsf{Wallet}} outputs a transaction report encrypted under the regulator’s public key. Otherwise, it outputs the encryption of zero. Therefore, the regulator is only allowed to learn about transactions that are determined to be illegal by C_{\textsf{AML}}. Moreover, since the users do not know the regulator’s secret key, they cannot distinguish the encrypted transaction report from the encryption of zero. Hence, from the indistinguishability of the SCO scheme, the obfuscation of C_{\textsf{Wallet}} is also indistinguishable from that of the contract circuit containing an AML circuit with output always 0, which leaks no information about C_{\textsf{AML}}.

Notably, our wallet service is vulnerable to regulators that allow the AML circuit to output 1 for every input. In other words, it cannot protect the users’ privacy from AML circuits determining that all transactions are illegal. How to prevent an AML circuit from excessively determining transactions as illegal while protecting their privacy is a future challenge.

Construction

Here is a basic idea of our construction of the SCO scheme.

Blockchain-based One-Time Program

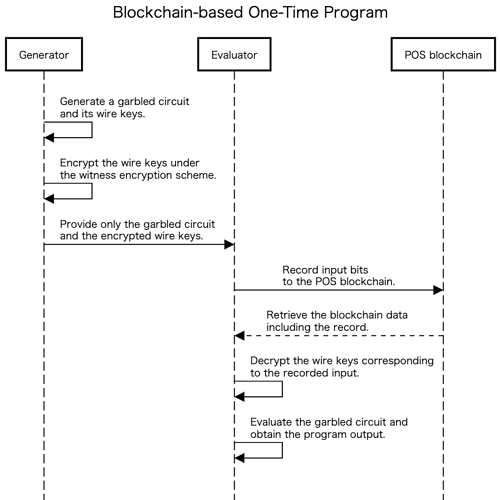
Our scheme is built based on one-time programs (OTPs) that use the POS blockchain. An OTP is a program that can be evaluated only on a single input specified at the evaluation time [31]. In other words, once an OTP has been evaluated, it cannot be evaluated on any other inputs. The first OTP construction proposed in [31] relied on trusted hardware called ``one-time memory (OTM)’’. Goyal [32] replaced the OTM with POS blockchain and extractable secure witness encryption (WE) and proposed a software-based OTP, which we call blockchain-based OTP (BOTP). In the BOTP scheme, a program generator compiles a program, and its evaluator records a single input onto the blockchain [32]. The valid blockchain data, including its record, allows the evaluator to evaluate the compiled program on that input. Its output is equivalent to that of the source program, but the evaluator cannot obtain any information other than the input and output of the program, provided the evaluator cannot remove the record from the blockchain. Thus, this scheme obfuscates the smart contract for only a single input.

Specifically, in addition to blockchain and the extractable secure WE scheme, the BOTP scheme uses a garbled circuit (GC) scheme as its underlying scheme (Figure 5). The GC scheme is a cryptographic technique for encoding a circuit and its inputs, whose encoded circuit, called a garbled circuit, reveals nothing except its output [33]. Its encoded inputs, called wire keys, are generated for each bit of the input, and the corresponding wire keys are necessary to evaluate a garbled circuit at a specified input. WE is an encryption scheme to encrypt a message to a particular problem instance in the NP language [8]. In the BOTP scheme, a program represented as a Boolean circuit is encoded to a garbled circuit, and its wire keys are encrypted under the WE scheme. We cannot directly release the wire keys for all inputs because the security of the GC scheme is only maintained for a single input. That is to say, an adversary that holds wire keys for two different inputs can learn the information on the circuit. These encrypted wire keys are decrypted if the blockchain data that only include a record of one input are provided. Therefore, the compiled circuit protects the privacy of the source circuit against the adversary who cannot remove the record from the blockchain.

Compiling BOTPs Multiple Times with Token-based Obfuscation

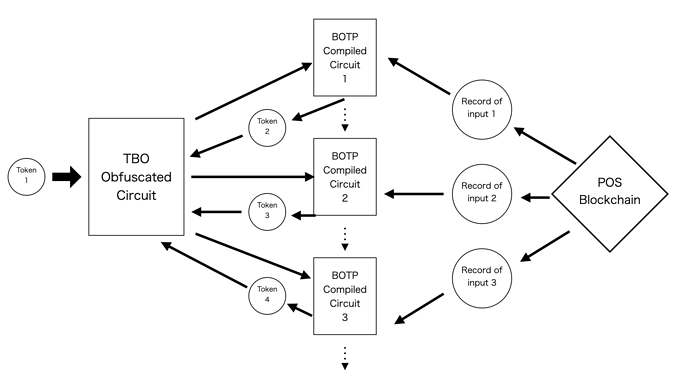
If a circuit compiled under the BOTP scheme can be evaluated on multiple inputs, such a scheme implies SCO. However, if its generator newly compiles a circuit for each evaluation, the scheme must continuously rely on that generator. In other words, if the generator terminates the compiling process, the evaluator cannot evaluate obfuscated smart contracts anymore.

To solve this problem, we execute the compiling process inside a circuit obfuscated under token-based obfuscation (TBO) [34] (Figure 6). TBO is a form of cryptographic obfuscation. The TBO scheme for polynomial-size circuits is constructed from fully homomorphic encryption (FHE), single-key attribute-based encryption (ABE), the GC, and symmetric key encryption (SKE), that is, cryptographic schemes, the securities of which are established under standard assumptions [34]. Unlike the BOTP scheme, the TBO scheme allows the evaluator to evaluate a single obfuscated circuit on multiple inputs. However, the evaluation requires a token corresponding to the input, which the generator of the obfuscated circuit can only generate with the obfuscation secret key [34]. Our idea is that a circuit obfuscated under the TBO scheme outputs a new circuit compiled under the BOTP scheme, and the compiled circuit generates a new token with the hardcoded secret key. The generator first publishes the obfuscated circuit and its first token. The evaluator then uses that token to evaluate the obfuscated circuit and obtains the first compiled circuit; its evaluation on a single input yields one output and the second token, allowing the obfuscated circuit to be evaluated again. Therefore, the evaluator can evaluate the circuit on multiple inputs by repeating this process, and the only process that requires a trusted generator in our scheme is the obfuscation process.

However, the above scheme still has two problems. First, it only proves secure only against a selective adversary that selects its input before seeing the compiled circuit; that is to say, it is selectively secure [32]. As an adversary can obtain multiple compiled circuits without interacting with the generator, our scheme requires the BOTP scheme to be secure against an adaptive adversary that selects its input after seeing the compiled circuit, that is, for it to be adaptively secure. Second, the running time of the token generation algorithm of the TBO scheme in [34] linearly depends on the output size of the circuit to be obfuscated, that is the size of the garbled circuit and its wire keys in our case. As the circuit to be obfuscated and the circuit to be compiled depend on each other, the size of the two circuits can not be determined simultaneously.

Establishment of the Adaptively Security with Functional Encryption

We solve the first problem by introducing an adaptively and single-key secure secret key function-private functional encryption (FE) scheme in the same way as [35]. In the secret key function-private FE scheme, a master secret key is used to encrypt the input and generate a secret key corresponding to the function [36-37]. That encryption and secret key combination only reveal the output for the input and function [37]. In our scheme, the process specific to each smart contract is computed using that FE scheme, and the circuit compiled under the BOTP scheme generates its secret key with the master secret key provided as input. The master secret key does not depend on the input to the smart contract; thus a selectively secure BOTP scheme is sufficient for the key generation process. As the FE scheme is secure against an adaptive adversary, this combination can establish the adaptively secure BOTP scheme and solves the first problem.

Notably, an FE scheme is sufficient in our scheme that is secure only if the same master secret key is used to generate a single secret key and the size of the ciphertext depends on the circuit size. Such an FE scheme is constructed from symmetric key encryption and the Pseudorandom generator (PRG) [37-38]. Hence, no additional assumption is necessary.

Establishment of the Compact Token Generation with Multikey FHE

For the second problem, multikey FHE (MKFHE) [39] is additionally introduced; in what is similar to the FHE scheme, participants can perform some computation on encrypted inputs. However, to decrypt the ciphertext, each participant must generate a decryption share using its secret key. The ciphertext is decrypted if and only if all shares are present.

Using the FE and the MKFHE schemes, we can securely separate the token generation algorithm into two parts: one depends on the secret key of the TBO scheme but its running time is independent of the output size m, and the other is vice versa. Specifically, the first algorithm takes a master secret key of the FE scheme as input and outputs a secret key corresponding to a function that on input an index i generates a token for the i-th output bit using the hardcoded obfuscation secret key. The second algorithm uses the same master secret key to encrypt an index i for all i in \{1,\dots,m\}. In our scheme, the first algorithm is evaluated inside the circuit to be compiled under the BOTP scheme, and the second one is performed by the evaluator that specifies the input. The evaluator can finally obtain tokens by decrypting the encrypted index using the secret key for the function. However, if a malicious evaluator knows the master secret key, it can extract the obfuscation secret key from the secret key for the function, which breaks the security of the TBO scheme. To prevent it, we encrypt the indexes via MPC of multiple evaluators. In more detail, each evaluator generates the fresh randomness and secret/public keys of the MKFHE scheme and encrypts the randomness under that public key. The evaluators then homomorphically evaluate a circuit that 1) derives the new randomness from the XOR of all provided randomnesses, 2) generates a new master secret key from the derived randomness, and 3) encrypts all indexes i under the master secret key. Each evaluator finally generates a decryption share with the evaluator’s secret key. From those shares, the encrypted indexes are recovered.

To prove that no master secret key is exposed, we have to assume that at least one of the evaluators is honest and disposes of the randomness after the MPC; otherwise, malicious evaluators can recover the randomness used to generate the master secret key.

State Preservation

An obfuscated smart contract can preserve states, and a malicious evaluator cannot use any state other than the latest one. This protection is achieved by encrypting the state under a one-time secret key of a symmetric key encryption (SKE) scheme.

For each smart contract, we define a nonce, a number that indicates how many times the obfuscated smart contract has been evaluated. The circuit compiled under the BOTP scheme internally generates two SKE secret keys corresponding to the current nonce and the next nonce and embeds them in a function evaluated in the FE scheme. That function, as its specification, takes the encryption of the current state, decrypts it with the SKE secret key for the current nonce, and outputs the new state encrypted with the SKE secret key for the next nonce. Since the states are encrypted with different secret keys, the user cannot use any state except the latest one to obtain the output of the function.

Notably, if the malicious evaluator knows the master secret key, it can obtain the embedded SKE secret keys from the secret key of the FE scheme. We prevent it in the same manner as the previous subsection, that is to say, multiple evaluators encrypt their inputs via MPC. If at least one of the evaluators is honest, no adversary can learn the other evaluators’ inputs or the SKE secret keys.

Separation of User and Evaluator

In the above description, the evaluator specifies the input and executes an obfuscated smart contract; however, these two processes are separated in our actual scheme. The user of the smart contract specifies the input and publishes its encryption. The evaluator uses it to evaluate the obfuscated smart contract and returns its output to the user, allowing the user to offload the heavy evaluation process to the evaluator.

Specifically, the obfuscator, referred to as the generator in the above description, generates a pair of secret and public keys for public key encryption (PKE). These keys are hardcoded in the circuit obfuscated under the TBO scheme and a circuit compiled under the BOTP scheme. The compiled circuit uses the hardcoded secret key to decrypt the provided encryption. For each nonce, the multiple users provide the inputs for the obfuscated smart contract as follows. First, each user generates the fresh randomness and secret/public keys of the MKFHE scheme and encrypts the randomness under that public key. The users then homomorphically evaluate an encryption circuit that 1) derives the new randomness from the XOR of all provided randomnesses, 2) generates two master secret keys from the derived randomness, 3) encrypts the master secret keys under the public key of the PKE scheme, 4) encrypts the indexes i under the first master secret key for all i in \{1,\dots,m\}, and 5) encrypts the provided users’ inputs under the second master secret key. Each user finally generates a decryption share using the user’s secret key, which only reveals those encryptions. One of those users recovers them from those shares and records the encrypted master secret keys onto the blockchain. The evaluator obtains a new compiled circuit from the circuit obfuscated under the TBO scheme and the latest tokens and then evaluates the compiled circuit using blockchain data. It outputs two secret keys: one is for the function to generate tokens and the other is for the function specific to each smart contract. The evaluator finally decrypts the encrypted indexes and the encrypted users’ inputs with those secret keys, which yields the new tokens, the outputs of the smart contract, and the new encrypted state. Informally, they leak no information beyond the outputs so that the users can allow an untrusted third party to evaluate the obfuscated smart contract.

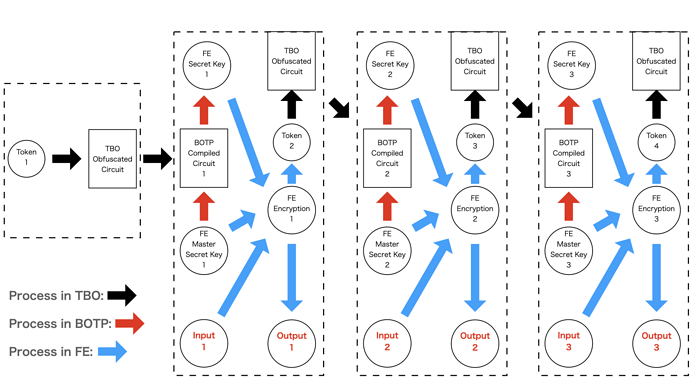
In summary, the obfuscated circuit is evaluated by repeating the following process. (Figure 7)

1. TBO evaluation: evaluate the circuit obfuscated under the TBO scheme with a token to obtain a circuit compiled under the BOTP scheme.
2. BOTP evaluation: evaluate the compiled circuit using blockchain data that includes the encrypted master secret keys. It returns secret keys corresponding to a token generation algorithm and a function of the smart contract.
3. FE decryption: decrypt the FE encryptions using the secret keys to obtain the new tokens and the outputs of the smart contract.
   
   

Security Analysis (Informal)

Our scheme depends on various cryptographic schemes, that is, the GC scheme, the WE scheme, the TBO scheme, the adaptively and single-key secure secret key function-private FE scheme, the MKFHE scheme, and some basic cryptographic schemes such as SKE, PKE, and PRG. Following previous studies, we can conclude that the above schemes except the WE scheme exist, assuming the existence of one-way function and the LWE assumption as follows.

• GC scheme. Yao’s construction of the GC scheme is based on the SKE scheme, which is constructed from one-way function [33,40].
• TBO scheme. The origin construction of the TBO scheme relies on the GC scheme, the SKE scheme, the FHE scheme, and the ABE scheme. The latter two can be established based on the LWE assumption [41-43].
• FE scheme. The FE scheme required in our scheme is constructed from SKE and PRG, both of which are constructed from one-way function [35,37,38].
• MKFHE scheme. The construction of the MKFHE scheme in [44] is based on the LWE assumption.

Using the above cryptographic schemes, we first construct an SCO scheme that satisfies input indistinguishability and then transform it into a scheme that also satisfies function indistinguishability. Informally, the former indistinguishability is proved as follows.

1. Assuming that at least one of the users is honest, the MPC performed by the users only reveals the encrypted master secret keys, the encrypted users’ inputs, and the encrypted indexes.
2. As an adversary cannot remove the record from the blockchain, the security of the WE scheme ensures that the wire keys are recovered only for a single input.
3. The security of the TBO scheme ensures that the obfuscated circuit does not reveal the randomness used to generate a garbled circuit and its wire keys.
4. As the adversary can obtain neither the randomness nor the wire keys for more than two inputs, the security of the GC scheme ensures that the garbled circuit reveals no information other than its output, i.e., secret keys of the FE scheme.
5. As the master secret key is not exposed, the FE scheme ensures that their ciphertext and secret key only reveal the circuit output.
6. As the outputs are indistinguishable, the adversary cannot distinguish between two encrypted inputs.

The input-indistinguishable SCO scheme is transformed into a function indistinguishable in a manner similar to that of the generic transformation of secret key functional encryption in [37]. An adversary that can break neither the security of the SKE scheme nor the input indistinguishability of the SCO scheme is also unable to break the function indistinguishability.

Conclusion

We developed smart contract obfuscation based on existing blockchain mechanisms, standard cryptographic assumptions, and witness encryption. It protects data privacy and function privacy for a wider class of smart contracts than NIZK-based privacy-preserving smart contracts. Unlike the SMPC and TEE-based solutions, it only requires an existing secure POS blockchain, e.g., the Ethereum blockchain, and MPC among users where at least one user is assumed to be honest. Notably, the user is not required to work after finishing a single MPC. If the MPC does not finish within a period of time, anyone can cancel and restart it to generate a new ciphertext. It also provides a decentralized obfuscation algorithm: MPC participants obfuscate one of two provided circuits whose outputs are indistinguishable. Unless all participants are malicious, no one can identify which circuit is obfuscated and learn secrets hardcoded in the obfuscated circuit.

The trustless bitcoin bridge mechanism that exposes no secret key and the privacy-preserving anti-money laundering built into smart contracts are the first applications that can be established with our scheme.

References

smart_contract_obfuscation_only_reference.pdf (42.3 KB)