With this post, I would like to introduce you to the rationale behind the Curvy protocol, a pairing-based stealth address protocol. You can find a detailed description of the Curvy protocol in our paper Elliptic Curve Pairing Stealth Address Protocols. For those who prefer reading a blog instead of the paper, you can check out our blog on this topic. I will try to answer all your questions in the comments!
Introduction
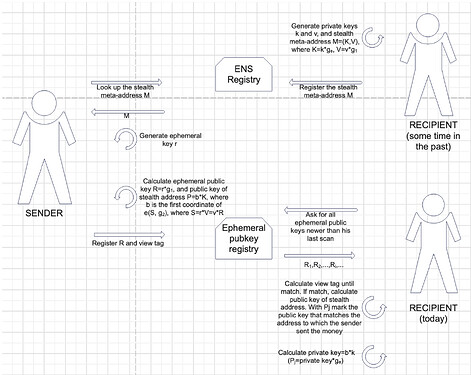
We can use different versions of the stealth address protocol. Some of them, such as DKSAP (Dual-Key Stealth Address Protocol), are based on a cryptographic mechanism similar to the Diffie-Hellman method, i.e. the private and public keys for the stealth address contain a shared secret that can be computed by both the sender and the recipient. DKSAP is explained in detail in Vitalik’s blog, and Vitalik also suggested SAPs based on pairing as one of the directions of stealth address research. Stealth addresses can be generated using another cryptographic method: elliptic curve pairing. In the papers EDKSAP: Efficient Double-Key Stealth Address Protocol in Blockchain and A New Stealth Address Scheme for Blockchain, SAPs based on pairing are presented. In the first paper, there is a gap that allows the sender and the person holding the viewing key to pair to obtain the private key of the stealth address. In the second paper, the private key of the stealth address is such that it can be computed by the sender without teamwork. We propose the Curvy protocol, which is based on elliptic curve pairing and overcomes these shortcomings.
Some of the optimizations we have made in the Curvy protocol (the reader can find more about them in our paper) can also be used to optimize DKSAP, while others cannot. The peculiarity is that the hash of the shared secret is not used to calculate the address in the Curvy protocol, but only for the view tag. Therefore, we can also use two bytes of the hash of the shared secret as the view tag, while using the same view tag would compromise the security of DKSAP. Note that in the Curvy protocol, we can also use the entire hash of the shared secret for the view tag without compromising security of the user.
Curvy protocol
Let e: \mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_T be elliptic curve pairing. Let g_e be the generator point of the elliptic curve Secp256k1, and let g_1 and g_2 be the generator points of the subgroups \mathbb{G}_1 and \mathbb{G}_2 of the elliptic curve BN254.
Curvy protocol is shown in a detail in the following figure:
Implementation results
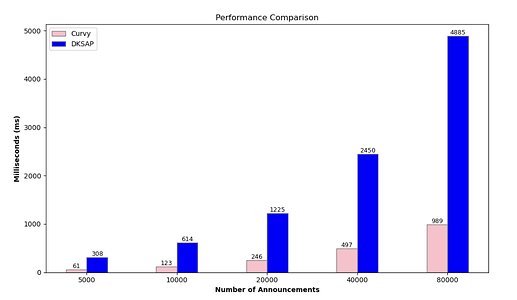
Since transaction speed is crucial from the users’ perspective, we aimed to create a protocol that meets their needs. For this reason, it was important to optimize the most sensitive part (which takes the longest) - the calculation of the new stealth address by the recipient of the transaction.
In our implementation of the Curvy protocol, we used the Go programming language together with the gnark-crypto library. The figure below compares the search times of the ephemeral public key registry for different numbers of announcements (5000, 10000, 20000, 40000 and 80000) of the Curvy protocol (with pairing-friendly curve BN254 and optimal Ate pairing) and the implementation of DKSAP from BaseSAP. The values of the private keys and the size of the view tag (5.5 bytes) from BaseSAP were used.
Useful links for further exploration: