Deliberative Decision-Making using Argument Trees

mheuer · August 21, 2021, 4:51pm

This write-up proposes a deliberative voting algorithm based on argument trees that could be used in DAOs and aims to produce more well-informed decisions.

Problem

Simple ballot protocols, such as single-choice, multiple-choice, weighted, and quadratic voting, are used for decision-making. However, decisions options might have far-reaching consequences that the voter is not aware of or misinformed about. Additionally, decisions might have many aspects, which the voter finds difficult to structure and weight because she/he is overwhelmed by the information. Moreover, voters often have no incentive to consider other aspects or perspectives outside their social bubble.
In this situation and due to lack of time and attention, voters tend to make gut decisions or follow leading figures. Populists can take advantage of the situation by influencing voters with misinformation strategies and emotionalization of the debate.

Instead of voting directly for or against the proposal (or several decision options), deliberative decision-making processes can be used, where people consider, rate, and weight different arguments for and against the proposal (or several decision options) in a debate.
Many connected problems (such as organizational overhead, high cognitive load for the audience, limited number of debate participants) can be reduced by conducting debates on Web2 platforms such as kialo.com (see an exemplary debate here).
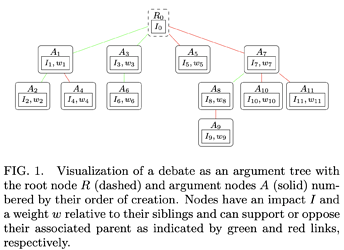
Starting from a proposal statement (e.g., ‘We should do A.’) forming the root of the debate,
participants structure the debate as a tree of pro and con arguments and rate their impact.
However, because Web2 platforms rely on centralized infrastructure and are prone to Sybil attacks they cannot be used for actual decision-making for obvious reasons: They

The aim is now to decentralize this debating process to be able to use it to make actual decisions.
In the following, the proposed voting algorithm is described.

Overview of the Decision-Making Process

Initially, the creator of the debate chooses the root statement and deposits a bounty to incentivize participation in the debate. This can either be reputation in the DAO or a monetary reward.

The voting algorithm consists of three phases:

an editing phase, where the argument tree is created and curated,
a voting phase, where participants are incentivized to rate and weight the impact of the arguments, and
a tallying phase, where impact rating and weighting of the arguments is accumulated from the leaves to the root of the tree to make the decision.

In the editing and voting phase, participants can spend debate tokens \text{T}.
In the beginning of a debate, these are issued to the participants (either equally or based on reputation in the DAO) and can only be used in this specific debate. Most importantly, they are not tradable.

Finally, participants that have performed above average and earned more debate tokens \text{T} than they have spend, earn a proportion of the bounty.
Accordingly, this process can be seen as the decentralization of the job of politicians and consultants.

1. Editing Phase: Curating the Argument Tree

In the editing phase, the goal is to construct and curate the argument tree to achieve a clear structure and resolve disputes between the participants.

Participants can occupy the following roles in the editing phase:

debaters, which author arguments, and
curators, which raise disputes about plagiarism/duplicates or inappropriate content (such as spam, hate-speech).

Jurors, which are excluded from participating in the debate to maintain neutrality, resolve disputes between debaters and curators in digital courts (such as Kleros Court).

Debaters have the option to edit, move, or delete their arguments within a given grace-period. Afterwards, the argument becomes finalized so that other debaters can post dependent arguments below. This gives them room to improve/clarify their arguments and accept suggestions.

A schematic example of a debate tree containing multiple, dependent pro and con arguments is shown below:

2. Voting Phase: Determining Argument Impacts via Rating Markets

After the editing phase, the whole argument tree is finalized and voters can rate the argument impacts.
Determining the impact of an argument is the key challenge. Here, the goal is to incentivize the participants to rate the impact I of an argument and to decouple this from the individual outcome preference.
In simple terms: Voting solely with the goal to influence the decision should be an unprofitable strategy.

One way is to use a modified version of a prediction market such as Omen that employs an AMM for liquidity provision. This picks up parts of the idea proposed in the post Prediction markets for content curation DAOs.
Accordingly, the impact rating of an argument is determined via an associated market.
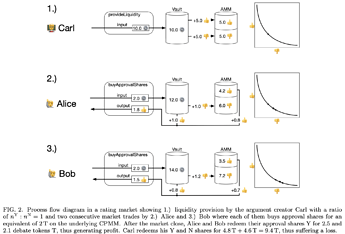
To realize this, each creator of an argument has to deposit an amount of debate tokens (\text{T}).
These tokens are then used to mint approval (\text{Y}) and disapproval (\text{N}) shares at a ratio that the creator chooses. The \text{Y} and \text{N} shares form a trading pair and their ratio determines the initial impact of the argument by

I=1-\frac{n^\text{Y}}{n^\text{Y}+n^\text{N}},

which can take values on the interval [0,1]. Accordingly, the less approval shares are available on the market, the higher is the impact I of the argument

Voters can invest their debate tokens to buy \text{Y} and \text{N} shares of under- or overrated arguments on the market, but have to pay fees to the argument author.
This mechanism incentivizes them to look for opportunities and to consider different arguments perspectives.

After the market closes, voters can redeem their shares for debate tokens. The author and liquidity provider gets the remaining debate tokens + fees.
If the author misjudged the impact of her/his argument initially, she/he suffers permanent loss.
If he misjudged the impact a lot, the loss can be larger than the fee revenues.
To prevent authors from knowingly posting bad arguments and rating them as such, the initial mint ratio can be limited to initial impacts I\in[0.5,1) so that large permanent losses are likely in this case.

An example is provided below:

3. Tallying Phase: Accumulating the Weighted Argument Impacts from the Leaves to the Root

After the voting phase ended and all markets are closed, the impacts of the arguments has to be weighted and accumulated from the leaves to the top of the tree. The weight of a node N_i can be defined by

w_i^{S} = \frac{n_i^\text{T}}{n_i^\text{T}+\sum_{j\in S_i} n_j^\text{T}}

as the amount of spent debate tokens n_i relative to its siblings S_i

This allows for expressing the impact of a node N_i by

I_i = \max \left[\vphantom{\sum}\right. \underbrace{(1-\gamma_i)\cdot I_i'}_{\text{own}} + \underbrace{\gamma_i\cdot I_i^{C}}_{\text{children}} , 0 \left.\vphantom{\sum}\right],

as two terms scaled with a mixing parameter \gamma_i. The first term contains the nodes own impact I_i' being determined directly from the associated rating market. The second term contains the weight-averaged impact of all children nodes

I_i^{C} = \sum_{j\in C_i} \sigma_j\,I_j\,w_j^{S}

with the pre-factor

\sigma_j = \begin{cases} +1 & \text{if node $j$ is supporting}\\ -1 & \text{if node $j$ is opposing} \end{cases}

resulting in the subtraction of impact, if the associated node opposes its parent.
The outer \max operator ensures that the overall impact value cannot become negative.

Both terms are scaled with the mixing parameter \gamma. The higher the value of \gamma, the more influence the children nodes have on I_i. Because the influence of a single node on the decision outcome decreases with increasing distance from the tree root, it becomes less attractive to add too many layers to the tree, which incentivizes keeping debates short.

Special cases arise for the different node types in the tree:

\gamma_i = \begin{cases} 1 & \text{if node $i$ is the root ($i=0$)}\\ 0 & \text{if node $i$ is a leaf}\\ k \in[0.5,1) & \rm{else} \end{cases}

For the root node, the impact is solely determined from the child impacts (\gamma=1).
For a leaf node, the impact is determined solely from its own rating market (\gamma=0).
For all other nodes, the ratio between the two is defined by a constant k\in[0.5,1) specified by the debate creator.

If the weight-averaged impact of the root node’s childrens is >0.5, the proposal is accepted. Otherwise it is rejected.

Attack Scenarios and Mitgation:

Spamming Attacks: The number of nodes that can be created is limited by the number of debate tokens and curators can remove the spam nodes not representing valid arguments.
Ownership Attacks: Duplicates and plagiarism can be identified by curators via the node’s time-stamp or ultimately decided by jurors in a court.
Sybil Attacks: Curated registries such as Proof of Humanity can ensure that only real humans participate.
Collusion: As in conventional voting algorithms, bribery or blackmailing can influence the decision. It can possibly be solved in the future by minimal anti-collusion infrastructure (MACI).

Open Problems:

Controversial arguments will attract the most debate tokens and result in the most fees for the authors.
The impact that an argument exerts on its parent can be diluted by creating more and more siblings. It is unsure if curation (removal of such arguments) can fully compensate this.
Decoupling the rating from the individual outcome preference is only possible if the individual reward for constructive participation is higher than the individual gain from influencing the decision to a certain outcome. It is unclear how to identify the right parameters.

Critical discussion is heavily encouraged, as there are likely many more flaws to be found.

Conclusion

By constructing a tree of pro and con arguments, voters are quickly onboarded and get a clear overview of the different aspects of a decision. Together with the rating and weighting of the arguments the reasoning behind a decisions becomes very transparent, which legitimizes the process by design.

Further Read:

For more details and updates, refer to the ArborVote whitepaper draft.