Designated Verifier Signatures

zk-s[nt]arks
1

Making Designated Verifier Signatures Compatible on Ethereum

This post is written in collaboration with @enricobottazzi. The GitHub for this project can be found here.

1) Motivation

As noted in the Plural Publics paper, deniable messages play a critical role in being able to establish and preserve context in human communication. The applications are well discussed in that paper, which was co-authored by one of us.

2) Definitions

A designated verifier signature is defined in the following way:

Instead of proving ɸ , Alice will prove the statement “either is ɸ true, or I am Bob. ”

The result of having the designation of verifiers is that only the designated verifier is convinced of the claim being made. In the example above, if Charlie is a third-party who is not involved in the claim being made, will not be convinced of ɸ if Bob is fully capable of proving himself to be Bob.

The key properties that a designated verifier signature satisfies includes:

  1. Unforgeability: the receiver should be convinced that the message actually came from the sender in question.
  2. Off-the-record, or deniability: the receiver cannot later prove to a third party that the message came from the sender.

If a designated verifier signature is being sent to multiple designated verifiers, it must also satisfy:

  1. Consistency: requires that if one recipient can verify a signature, they all can.

3) Circuit Design

1600Ă—713 102 KB

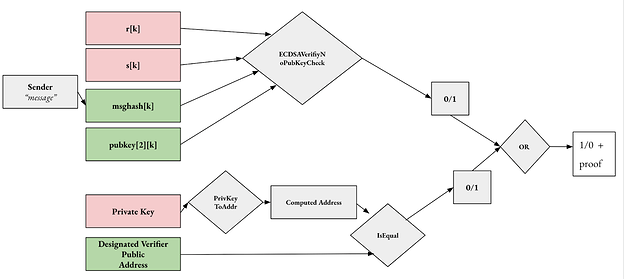
Figure 1. Circuit design for two-person designated verifier signature messages where red are private inputs and green are public.

We will work through the design of the circuit shown in Figure 1 from top to botoom. The first part of this circuit is focused on the elliptic curve digital signature algorithm (ECDSA) and the ECSDAVerifyNoPubKeyCheck circuit component respectively. This function was taken from Ethereum 0xPARC research organization’s ECDSA circuit library where they have implemented this function in Circom.

The compiler outputs the representation of the circuit as constraints and everything needed to compute various different zkSNARKs. This circuit takes a signature, with private inputs (r,s), a message hash, and a secp256k1 public key. It follows the ECDSA verification algorithm to extract r’ from s, message hash, and public key and then compares r’ with r to see if the signature is correct. The output result is 1 if r’ and r are equal, and 0 otherwise. So far, in the top part of the circuit, this function knows whether or not the message was in fact digitally signed by the sender of the message.

The bottom part of this circuit uses a function also created by 0xPARC in their ECDSA circuit library where they have created a circuit ECSDAPrivToPub which is also written in Circom. This circuits takes a secp256k1 private key, and will output the corresponding public key by computing G * (secp256k1 private key) where G is the base point of secp25k1. If the public key matches the designated verifier address public address, then the circuit will output a 1 and otherwise output a 0.

These two parts of the circuit are combined by an OR gate such that it is unclear to a third-party as to which part of the circuit satisfied the condition of the OR gate: the message was actually digitally signed by the sender or the designated verifier falsified the claim. To the designated verifier however, if the output of the circuit is a 1 and they did not pass their secp256k1 private key, it must be the case that the message was digitally signed by the sender. As the designated verifier, they are the only individuals who are convinced by this information.

4) Making DVS Compatible On-Chain and Off-Chain

In this section we outline how DVS could be made compatible with existing key generation algorithms both off-chain and on-chain.

The first part of the implementation for both off-chain and on-chain solutions is quite similar and goes as follows:

4.1 DVS Setup

Alice wants to send a message to Bob. Only Bob should be convinced by this message, and a 3rd party, Charlie, should not.

  1. The trusted setup and application protocol is already complete such that any user can generate a witness and a proof. The WASM file, proving key, and verification key are accessible for both message senders and receivers to be used for their respective actions.
  2. Alice connects their EOA to the messaging platform.
  3. Alice types the message in the platform that is only storing the information locally.
  4. Alice inputs the designated verifiers public address, here that would be Bob along with Bob’s private key. If Alice does not know Bob’s private key, which in most instances they wouldn’t, a randomly generated private key is the default input.
  5. Alice is prompted by a wallet to sign the message with their private key to generate the signature, following the standard of EIP-191.
  6. Alice generates a witness with the inputs of the circuit along with the WASM file.
  7. Alice generates a proof with the witness, WASM file, and proving key. Proof.json and public.json are generated which contain the proof and the public inputs to this proof.

Now that the proof has been generated is where we get to looking at how this could be put on-chain or off-chain.

4.2 DVS Protocol Off-Chain

If Alice wants to use an off-chain solution but still notify Bob, here are the following steps.

  1. Alice publishes the proof.json and public.json on IPFS whereby the message is encrypted but everything else stays as is.
  2. The messaging protocol keeps a database of the CID’s posted on IPFS that originate from the network.
  3. For a new CID that was added to IPFS, the network sends a notification to the designated verifier (identified by their address) with this CID.
  4. This designated verifier can open this message, and will use the verification key from the trusted setup to verify the message.
  5. The designated verifier is convinced of the message.

For the on-chain solution, there is more work to be done prior to the message being posted to the network. This includes creating a verifier smart contract and funding a relayer. By funding a relayer, we mean that the messaging network must subsidize all of the transactions to be sent on this relayer. An out-of-the-box relayer solution is offered by Openzeppelin Defender. A Defender Relayer is an Ethereum account that would be assigned to the instantiation of the messaging network. Every time you create a new Relayer, Defender will create a new private key in a secure vault. Whenever you request Defender to send a transaction through that Relayer, the corresponding private key will be used for signing. The specs of the Defender can be configured such that it will only execute transactions to a specific smart contract, in this case the Verifier Smart Contract deployed previously. This relayer is a queue for sending transactions, where all transactions sent through the same Relayer will be sent in order and from the same Ethereum account, controlled exclusively by the messaging protocol. The purpose of this is to ensure that people can’t see where the transaction is coming from which would otherwise publicly reveal the identity of the signer of the message and nullify the purpose of the scheme .

4.3 DVS Protocol On-Chain

If Alice wants to use an on-chain solution but still notify Bob, here are the following steps.

  1. The messaging protocol deploys a Verifier Contract
  2. Alice sends proof.json and public.json (formatted into solidity Calldata) to the Verifier Contract using a relayer
  3. This transaction calls the verify function in the verifier smart contract that will output true or false according to the validity of the proof.
  4. In the verifier smart contract, an event is emitted of which can be indexed. Here, Bob is notified of the corresponding proofs his designated address is part of, and convinced of the message if True.

5 Future Work and MDVS

Multi-designated verifier singatures (MDVS) is an extension of designated verifier signatures to the multiparty setting. As outlined in this paper, the key properties that an MDVS signature scheme aims to follow in addition to the foundational properties of a DVS (unforgeability and off-the-record) include:

  1. Privacy of Identities (PSI): The message signature should not reveal the message sender or receiver’s identities (public key). When the signer’s identity is hidden, then PSI is satisfied.
  2. Verifier-Identity-Based (VIB) Signing: The sender should only require the designated verifier’s identities (public address), and not necessarily their public keys in order to produce the designated verifier signature.
  3. Consistency: Even if the sender is malicious, if one of the designated verifiers can authenticate that the message came from the sender, they all can.

To enforce MDVS, introduce provably simulateable designated-verifier signatures (PSDVS) which enables a non-interactive zero-knowledge (NIZK) proof to show whether all DVSs are real or they are all simulated. One previous iterations of MDVS include issuing a separate DVS for each designated verifier. A limitation of this design is in the consistency property by which the sender can issue some verifying DVS and others that do not verify (ie., simulations). Other solutions could be to include a NIZK that all designated verifiers can verify. However, the limitation with this model is that simulation is not possible without all of the dwarves present.

Other areas of improvement include:

  1. Performance: Currently the circuit comprises of 1.7M constraints and the proving time is around 5 mins
  2. User Experience: A malicious designated verifier needs to manually input their private key to generate a valid proof, which is not secure or even unfeasible in the case of hardware wallets.
  3. Currently, the part “Alice owns 1000 ETH (#1)” is not an any arbitrary statement but only supports signature verification. It would be cool to make the DVP as an independent circom component that can be easily plugged into any existing circuit. It could work like “I know the signature of the designated verifier” rather than “I know the private key of the designated verifier”. This is mainly for UX and security reasons and it is always advisable not to deal with plain private keys.
  4. Efficient ECDSA: Reeplace 0xParc’s circom-ecdsa with more efficient ECDSA signature verification protocol such as Personae Labs Spartan ECDSA.

Please feel free to reach out to either of the authors of the post for questions about our implementation or how to get involved with other work.

4 Likes
2

Hey, guys! Thank you for this proposal and for all your work, that looks impressive and sounds exciting.

I’m wondering if DVS is enough for “true” resilience? What I mean by that is for “either is ɸ true, or I am Bob” the third party has probability 0.5 to guess the right answer. Can we decrease this probability by wrapping this mechanism into something else? Just thinking out loud – repeating this enough times. Or to have a solid practical implementation we need MDVS?

I’m also wondering what use cases you feel the most fitting for DVS implementation, as you’ve mentioned using ID instead of Private Key maybe you have specific protocols in mind and ready to share?

Finally, I didn’t get to the end how Bob will know that the private key is his private key – if we speak about the case when Alice doesn’t know Bob’s private key and a new private key is generated.

3

Can you pls gib some examples for what this would be useful for?

1 Like
4

hi @sthwnd, @monkeyontheloose

sorry for the late reply, but better later than never :smiling_face_with_tear:

An option could be to replace the lower part of the circuit with a gate that checks that the address that maps to the private key belongs to a certain membership set that would represent the set of designated verifiers. So the DVS will now prove that “either ɸ is true, or I am a member of that set”. Now let’s consider an example where Alice wants to share a signed message with a designated group composed by Bob and Carl and broadcasts a DVS. People from the outside will be more “confused” as the possible right answers are now 3. But the problem is that also Bob and Carl are also confused about the provenance of the message. From Bob point of view, it can be either “ɸ true, or the proof has been generated by Carl”

I think that the most compelling use case is for communication when you want to achieve deniability of the message. Considering a message that is broadcasted using a DVS, a message receiver cannot convince a third party about the real provenance of that message

I believe that you are referring to point 4 in the DVS Setup 4.1. This is the case where Alice is sharing a DVS to Bob. The core assumption here is that Bob’s private key hasn’t been leaked and Bob is certain that his private key hasn’t been leaked. If we rely on this assumption, Bob knows that the author of the DVS cannot have used his private key as input to the circuit and therefore the proof must verify because ɸ is true. Note that here we use a random private key as input just because a private key must be passed as input.