If a protocol doesn’t require explicit endorsement of a block to reach consensus and just rely on other factors such as PoW, it is possible to disclose blocks much later and alter the course. Many PoS protocols require direct interaction with each other to reach consensus, using a variation of pBFT (practical Byzantine fault tolerance). Immediate direct interaction ensures consensus is discovered quickly and it will not be possible to release blocks at a later time. This makes these protocols to be almost deterministic compared to what is possible with Bitcoin for example. When multiple blocks can be proposed for a given round, it is sometimes possible to not be able to determine if a block is finalized because of network conditions. This is where protocols such as Hashgraph take a different approach. They rely on the fact that the current proposals are consistently endorsing past transactions and when a majority of the miners endorse directly or indirectly a given transaction, it gets finalized. Transactions get finalized individually but the same concept can be applied at the block level. That is, when enough miners extend directly or indirectly off of a given block, it is possible to agree on which of the notarized blocks in a round should be finalized deterministically. 0Chain executes finalization based on locally available information but also keeps track of the deterministic finality using the Hashgraph like logic applied at the block level. In our experiments we have not seen any rollbacks of finality computed based on local information even after running the blockchain for hundreds of thousands of blocks. The clients interacting with 0Chain have several choices on deciding on when to consider their transaction is finalized. They can choose to wait a certain number of blocks, they can choose to query the confirmation from multiple nodes or do a combination of both.
In 0Chain, there are three blocks that are of interest. They are:
The block that is being added to the current round
The block that is probabilistically finalized using a variant of dFinity algorithm
The block that is deterministically finalized using a logic explained below.
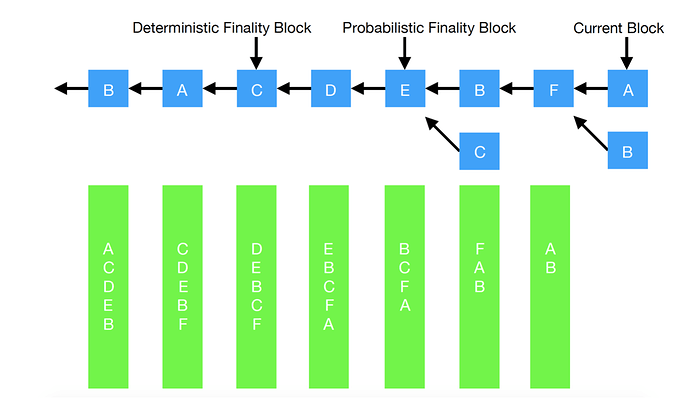
It should be noted that the deterministic finalized block lags the probabilistic finalized block which lags the current round block (If all miners generate, then it is possible to have deterministic finality as fast as probabilistic finality).
When a miner receives a block for a round and it is from a valid generator for that round, it is added to the local cache of blocks. During that time, the chain from that block is walked back till the previously identified latest deterministic finalized block. For each block in between, it is added to unique extensions map of the block if the miner of the current block hasn’t extended any block between this intermediate and current block. After sufficient progress of the chain, at some point each block that is probabilistically finalized will receive enough number of unique extensions, indicating that sufficient number of miners are working on top of that block. At that point, the block becomes deterministically finalized. The threshold used for deterministic finality will be the same as the threshold used for notarization of a block. For example, for a 3*f+1 miners with f number of Byzantine miners, there should be more than 2/3rd unique block extensions for a block to be considered finalized deterministically.
The diagram below indicates the above explained process. The letters in the block indicate the miner who generated the block. The letters in the green boxes below represent the unique chain extension endorsements for those blocks. Also shown are additional block proposals C and B received in a particular round.
Let’s assume that receiving 5 unique extensions is considered as the threshold. As soon as block from A is received in the current round, the block by D becomes finalized deterministically as A gives an extra unique endorsement. Similarly, when block from B is received for current round, the block by E becomes deterministically finalized. So the deterministic finality moves from C to E. And so, having more generators (leaders) help accelerate deterministic finality, albeit with an increase in network traffic.